Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Las matemáticas no solamente poseen la verdad, sino la suprema belleza, una belleza fría y austera, como la de la escultura, sin atractivo para la parte más débil de nuestra naturaleza.
Bertrand Russell
Dentro de las publicaciones que he tenido a bien realizar en estos Suplementos Culturales LaHora, se encuentra una, en los inicios, en la cual llevamos a cabo una primera aproximación a la temática de los espacios multidimensionales, es decir, hacia aquellos que poseen una dimensión n, con un n ∊ ℕ, siendo n > 3. Específicamente, fue en el artículo «Objetos multidimensionales» en donde dimos unas primeras pinceladas al respecto. Resulta que la motivación inicial para abordar el tema derivó del caso de que la matemática ucraniana Maryna Sergiivna Viazovska fuera galardonada con la prestigiosa Medalla Fields, por sus valiosos y notables aportes sobre el empaquetamiento de esferas.
Aparte de tratarse de una mujer matemática brillante, lo que a muchas personas pareciera no ser lo usual, los tópicos merecedores del reconocimiento son interesantes por sí mismos. Este problema que mencionamos, concerniente al empaquetamiento de esferas, se refiere a una particular problemática de valores extremos, en la que se persigue encontrar la mejor disposición que una colección de esferas de idéntico tamaño debe asumir para rellenar, de forma óptima, un determinado espacio, entiéndase, con el máximo de esferas, dado el volumen, o bien, con el mínimo espacio, fijando la cantidad de esferas.
Es relevante mencionar que el astrónomo y matemático alemán Johannes Kepler planteó una conjetura con relación al caso tridimensional, la que perduró durante varios siglos antes de poder ser demostrada. El asunto de fondo es que el problema de empaquetamiento puede generalizarse a espacios n-dimensionales, en donde se concibe a las hiperesferas de una forma matemática bien definida. A Viazovska se le concedió el citado premio porque resolvió el problema del empaquetamiento en la dimensión 8. Al respecto de su trabajo y del reconocimiento, en la Wikipedia se lee:
En el año 2016 [ la ucraniana Maryna Viazovska ] solucionó el problema del empaquetamiento de esferas en la dimensión 8 y, en colaboración con otros, dentro de la dimensión 24. Anteriormente, el curioso problema había sido resuelto solo para tres o menos dimensiones, y la prueba de la versión tridimensional, conocida como la conjetura de Kepler, implicó largos cálculos de ordenador. Por contraste, la prueba de Viazovska para 8 y 24 dimensiones es «sorprendentemente sencilla». Fue galardonada con la Medalla Fields en el año 2022, otorgada por la Unión Matemática Internacional, por su específico trabajo del empaquetamiento de esferas en la dimensión 8. Ha sido la segunda mujer, después de la iraní Maryam Mirzajani, que gana esta prestigiosa medalla.
En el citado artículo, se desarrolló una introducción a la generalización de este concepto matemático de la dimensión de un determinado espacio. Queremos ahora dar oportuno inicio a una serie de publicaciones que le den continuidad a estos conceptos, no solo desde el abordaje matemático propiamente dicho, geométrico o algebraico, sino también sobre la interpretación estadística en la nueva Ciencia de Datos y desde el marco de referencia de la Física. Ya anteriormente hemos desarrollado alguna correlación entre los conceptos matemáticos per se y su posible aplicación en las distintas ciencias físicas, como en el caso del artículo «Discontinuidades obscuras e imposibles».
A propósito de la frase del epígrafe, que habla sobre la suprema belleza de la Matemática, conviene recordar que Bertrand Arthur William Russell fue un filósofo, matemático, lógico y escritor británico, ganador del Premio Nobel de Literatura, por lo que no es de extrañar el símil y la metáfora en sus palabras, cuando describe el quehacer matemático. El citado Johannes Kepler lo explica de manera parecida: «deseaba ser teólogo, pero ahora me doy cuenta, a través de mi esfuerzo, de que Dios también puede ser celebrado por la astronomía». Sobre nuestra posible intuición al respecto de estas ideas, el eximio matemático y físico suizo, Leonhard Paul Euler solía decir: «mejor que de nuestro juicio, debemos fiarnos del cálculo algebraico».
Después de este breve prólogo a nuestra bien intencionada serie de artículos, que tratarán sobre la dimensionalidad de los espacios y de los objetos en ellos, entraremos en materia empezando por una revisión de las nociones relacionadas con la medida de los diferentes cuerpos que percibimos en los espacios usuales, entiéndase, los de una, dos o tres dimensiones, las que intuimos y procesamos mediante nuestros sentidos. Para ello, conviene recordar que en estos mismos Suplementos Culturales LaHora, presentamos el proceso y los razonamientos mediante los cuales Arquímedes de Siracusa, erudito geómetra griego, procedió exitosamente al cálculo del volumen del cono, a través de una singular técnica, conocida por la posteridad como el método de exhaución.
Para esta precedente ocasión mencionamos que, con estos aportes, Arquímedes pasó a convertirse en el precursor del cálculo integral moderno, esto allá en la antigua Grecia del siglo II a. C., mucho tiempo después de las primeras sistematizaciones matemáticas de la escuela pitagórica y de los discursos de los filósofos presocráticos, quienes, como particular, llevaron a cabo las primeras consideraciones reflexivas sobre el infinito, como es el caso de Anaximandro y lo ápeiron, aquello que no tiene límites. Muchos sofismas y paradojas fueron obtenidos mediante argumentos racionales contradictorios, al pretender controlar esta infinitud, sea lo infinitamente grande, o bien lo infinitesimal, lo infinitamente pequeño.
Ya en la modernidad, estamos trayendo a colación a un matemático italiano menos conocido, discípulo de Galileo Galilei, quien en los primeros años del siglo XVII y en la misma línea de trabajo geométrico generó un principio por medio del cual iba a ser posible sistematizar las ideas del matemático siracusano, desarrollando un método al que llamó el método de los indivisibles, antesala de los infinitésimos, que aparecerían pronto con los trabajos casi simultáneos de Isaac Newton y Gottfried Leibniz, con los que aparecerían las notaciones y los cimientos de los futuros teoremas. Estamos hablando del matemático incluido en el titular, Bonaventura Cavalieri, clérigo de la orden de los jesuatos.
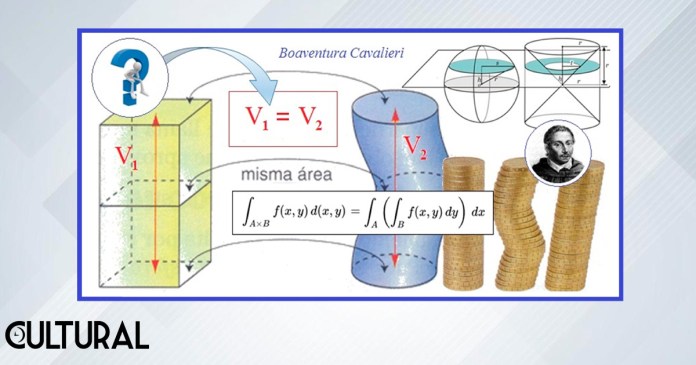
Los jesuatos fueron una orden religiosa, también llamada de los Clérigos Apostólicos de San Jerónimo, la cual no debe confundirse con la posterior y más conocida de los jesuitas. A Cavalieri se le conoce por el principio infinitesimal epónimo, es decir, que lleva su nombre. En forma muy sencilla y elemental, el principio de Cavalieri establece que, si dos cuerpos tienen la misma altura y al cortarlos por planos paralelos a sus bases se obtienen figuras con la misma área, entonces deberán tener el mismo volumen. Estas figuras que se obtienen al cortarlos transversalmente se denominan secciones. Así, de manera aún más breve, se dice que a secciones congruentes corresponden volúmenes iguales.
Puede visualizarse el principio, que resulta muy intuitivo, pero nunca antes había sido explicitado, considerando pequeñas rebanadas de los cuerpos en cuestión, esto es, tomando discos muy delgados, de forma casi cilíndrica, razón por la cual, inclusive actualmente, se le hace referencia como del método de los discos infinitesimales. La imagen que sigue muestra la idea básica, al yuxtaponer verticalmente una cierta cantidad de monedas, siendo cada moneda congruente entre sí.

Cavalieri fue el primero en introducir en Italia el cálculo logarítmico, en su cátedra de Matemática de la Universidad de Bolonia, la cual obtuvo a los treinta años de edad, pero debe su celebridad a esta teoría de los «indivisibles» que estamos mencionado. Específicamente, expuso el método en su obra Geometria indivisibilibus continuorum quadam nova ratione promota, en 1635, en la cual se estudia a las magnitudes geométricas, léase cuerpos tridimensionales y superficies bidimensionales, como compuestas por un número infinito de elementos, infinitesimales, a los que denominó los indivisibles, que son los últimos términos de la descomposición que se puede hacer.
Vemos aquí plasmada y operacionalizada la misma idea que Demócrito de Abdera hiciera en sus planteamientos atomistas al respecto de la composición de la materia, precisamente conformada por átomos. Recuérdese que átomo significa, literalmente, sin división, sin partición, lo que viene a ser equivalente a «indivisible». Lo interesante en Cavalieri es que sistematizó el cálculo de las medidas de los cuerpos, sin importar el número de dimensiones que los caracterizaran. Así, de esta manera, la medida de las longitudes de los objetos unidimensionales, de las áreas de las distintas superficies, bidimensionales, y de los volúmenes de los cuerpos, en nuestro mundo sensible tridimensional, se transforma en un mismo proceso, exhaustivo.
El proceso mencionado consiste en efectuar, analíticamente, la suma de una infinidad de indivisibles, lo cual pasará pronto a convertirse en el proceso de la integración del Análisis Matemático moderno. De hecho, el principio de Cavalieri describe el principio del cálculo de una integral definida, aunque sin el uso de la noción rigurosa contemporánea del paso al límite por medio de la topología de los espacios métricos. Por esto, Cavalieri y su principio pueden ser considerados como los precursores más sólidos del análisis infinitesimal propio de la Modernidad, siendo de tal importancia que su publicación marcará el comienzo de una nueva era en la historia de la Mecánica Celeste, ícono epistemológico del determinismo característico de esta época de la humanidad.
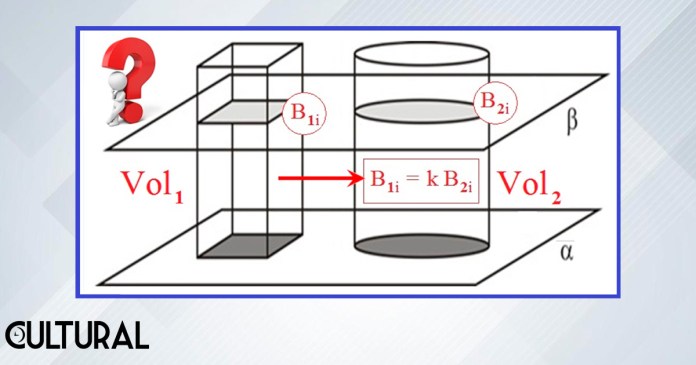
En su forma mejor conocida, la versión tridimensional, el principio de Cavalieri establece que, si las secciones paralelas de un cierto cuerpo mantienen la misma proporción con cada una de las secciones correspondientes de otro cuerpo mejor conocido, el volumen de estos cuerpos mantendrá la misma proporción que las secciones observadas, de forma tal que, si se conoce el volumen de uno de los cuerpos, se podrá, también, conocer el volumen del otro.
Por ejemplo, en la imagen precedente se muestran dos prismas rectos, uno de base cuadrada y otro de base circular. Ser prismas rectos significa que las secciones paralelas obtenidas son siempre ortogonales, perpendiculares, a una recta fija, a la cual se le puede identificar como el eje de cada prisma, de manera que cada sección así obtenida son denominadas secciones rectas. Sin embargo, esta restricción de ortogonalidad no será necesaria en el caso más general.
Como ejemplo, si cada círculo del cilindro circular recto es equivalente a un 20 % más que su correspondiente cuadrado del prisma ubicado a la par, es decir, si cada sección circular tiene un área igual a 1.2 veces el valor del área del cuadrado que le corresponde en el prisma de base cuadrada a la par (ie k = 1.2), se tendrá necesariamente que el volumen del cilindro circular será justamente 1.2 veces el valor del prisma de base cuadrada.
Este principio no aplica únicamente a cuerpos obtenidos del desplazamiento dinámico ortogonal de una superficie para generar un cuerpo tridimensional, sino de cualquier cuerpo, entiéndase n-dimensional, como podremos ver después, a lo largo de una determinada dirección fija, es decir, en línea recta. Por ello aplica también a áreas obtenidas por el desplazamiento de un cierto segmento de recta.
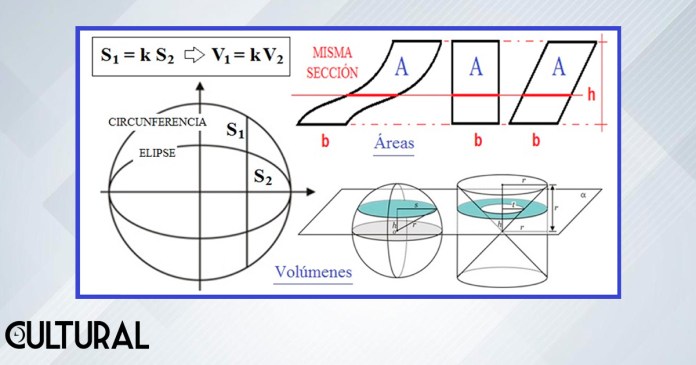
En la imagen precedente se muestra, a manera de otro ejemplo, el caso para el volumen de la esfera, ya abordado en artículo anterior, así como del área en dos ejemplares, en la parte superior derecha. Ahí se aprecia un segmento de medida b que se desplaza de tres maneras diferentes. El principio establece que el área, la medida del cuerpo resultante, es igual para cada uno de los tres casos.
Por otro lado, en la izquierda de la imagen, se muestra una elipse, la cual se obtiene de escalar la sección de la circunferencia asociada. Si el factor es, digamos, k = ½, se tendrá que la elipse tiene un área, el volumen bidimensional, cabal de k veces el área del círculo, o sea, en este caso, de la mitad del área del círculo generador, dado que k = ½. Por lo anterior, el principio puede enunciarse así:
- Caso bidimensional: supóngase que dos regiones de un plano, figuras planas, están incluidas entre dos rectas paralelas en ese plano. Si cada recta paralela a estas dos rectas interseca ambas regiones en segmentos de recta de igual longitud, entonces las dos regiones tienen áreas iguales.
- Caso tridimensional: supóngase que dos regiones del espacio tridimensional, cuerpos sólidos, están incluidas entre dos planos paralelos. Si cada plano paralelo a estos dos planos interseca ambas regiones en secciones transversales de igual área, entonces las dos regiones tienen volúmenes iguales.
- Caso n – dimensional[generalización del principio]: supóngase que dos regiones del espacio n – dimensional, es decir, n – sólidos, están incluidas entre dos hiperplanos paralelos, de dimensión n – 1. Entonces, si cada hiperplano paralelo a estos dos planos interseca ambas regiones en secciones transversales de igual tamaño, de volumen n – 1 dimensional, entonces las dos regiones tienen volúmenes n – dimensionales iguales.
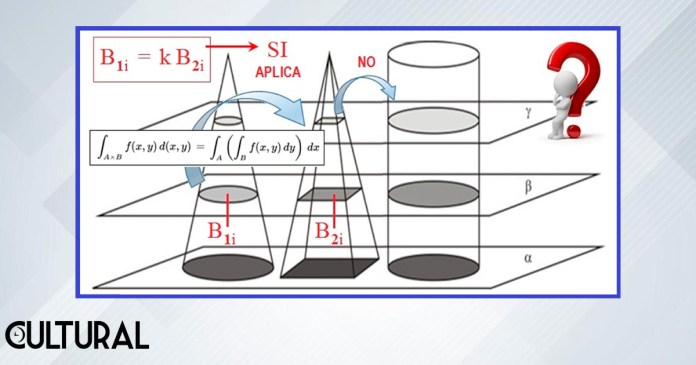
En el caso de un cono o un triángulo generalizado, el principio de Cavalieri no aplica, pues no hay forma de establecer una proporción constante entre las secciones. Así, en la imagen siguiente, el cono y la pirámide se pueden correlacionar, pero no así estos dos anteriores con el cilindro. Ameritará proceder a la extensión de este primer material para los casos en un espacio general, es decir, de n – dimensiones.
Así, se aprecia que el concepto de la dimensionalidad de un espacio que sea más general que el que intuitivamente reconocemos como el nuestro, físico y tridimensional, se encuentra caracterizado, entre otras cosas, por las medidas del largo, ancho y alto de los cuerpos que coexisten con nosotros. Estos otros espacios, no tan intuitivos, son el resultado de la abstracción matemática que podemos aplicar sobre las tres dimensiones que perciben nuestros sentidos como independientes, de forma tal que, al aislar la frontera de un cuerpo dado, y visualizarla como una superficie, es posible imaginarnos un espacio reducido en el que esta existe.
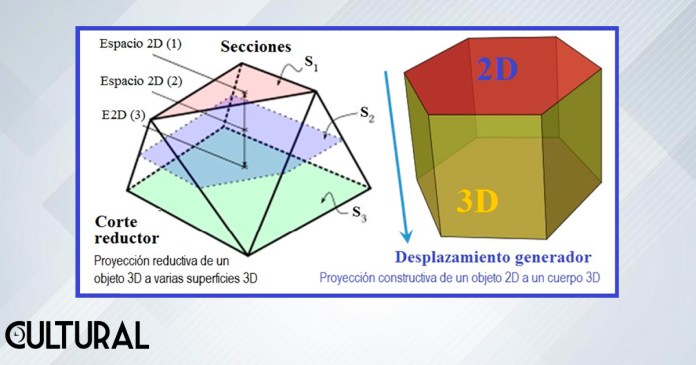
Observamos así que, en este espacio reducido, se tienen únicamente dos sentidos de libertad, pues, al imaginarlo de un espesor «infinitamente delgado», identificamos solo dos direcciones independientes, afirmando que se trata de un espacio bidimensional, es decir, conformado y descrito exclusivamente por dos dimensiones. Una hoja de papel ideal, que no tuviera grosor, o la superficie de una mesa muy lisa, son evocaciones mentales de un espacio 2 – dimensional. Simultáneamente, nuestra mente es capaz de establecer la relación entre estas dos geometrías, de manera que podemos obtener un espacio bidimensional «aplastando» los cuerpos tridimensionales, u obtener el espacio tridimensional «trasladando» los objetos bidimensionales en distintas direcciones, para otorgarles una dimensión extra a las dos que ya poseen, convirtiéndolos así en objetos tridimensionales.
Sin entrar en mayores formalizaciones, podemos utilizar el término proyección para referirnos a ambos procesos, uno en el que partiendo de un objeto 3 – dimensional, un cuerpo, lo reducimos a otro 2 – dimensional, una superficie, y otro que tomando un objeto 2 – dimensional, plano, lo convierte en otro 3 – dimensional, ampliándolo, mediante movimiento o traslación en una dirección independiente a las dos previamente consideradas, generalmente en dirección ortogonal (perpendicular) a la superficie inicial. Cabe anotar que usualmente entendemos por proyección el primer proceso, reductivo, que va de tres a dos dimensiones, temática tratada por la geometría proyectiva, de la cual la geometría descriptiva es un capítulo.
Con esta dinámica geométrica es posible ir de un espacio a otro, reduciendo o ampliando, de manera que podemos definir los espacios n – dimensionales, para un entero n ≤3, pero también imaginar espacios en los que se han agregado más dimensiones, ampliando por traslación o desplazamiento hacia otras direcciones independientes, por ejemplo, ortogonales, a las inicialmente consideradas. Este método generador por medio de proyecciones establece lo que se conoce como un espacio euclídeo n – dimensional, denotado por En, que algunos identifican como Rn, para un n ∊ ℕ cualquiera.
Más formalmente se trata de un espacio vectorial completo, o real, provisto de un producto interno, o producto punto entre vectores. Sin embargo, también es posible definirlo sobre un dominio entero o integral, como lo es Z, de forma que se asocia con una estructura algebraica de módulo, de naturaleza discreta, como un retículo, lo cual es especialmente útil en las nuevas ciencias de la computación.
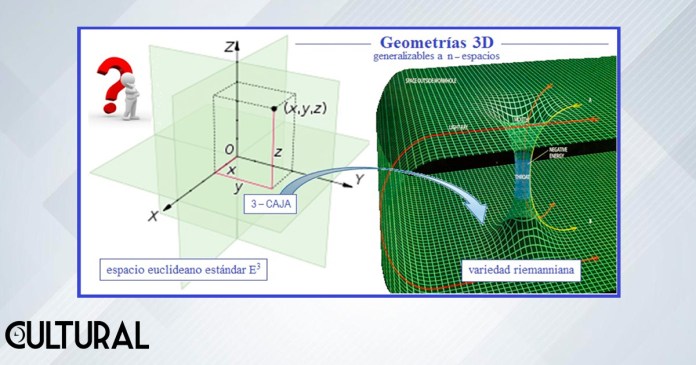
Los espacios euclídeos son de naturaleza lineal, por ser espacios vectoriales, lo cual facilita la definición de las estructuras matemáticas fundamentales necesarias en los modelos y teorías científicas, principalmente de la física teórica y las ciencias naturales cercanas. Básicamente, el producto interno, espacio Hilbert, induce una norma o tamaño, espacio Banach, que a su vez induce una métrica o distancia, espacio métrico, que le provee al espacio de una estructura topológica, esto es, espacial, además de la algebraica, vectorial, inicialmente otorgada.
El término euclídeo se utiliza generalmente para distinguir estos espacios lineales de otros espacios de alguna manera curvos, propios de las geometrías no euclidianas, utilizados en la mecánica relativista y otras formulaciones físicas, en las cuales el concepto de variedad riemanniana resulta esencial para la descripción. De forma sobresimplificada, una variedad de Riemann es una que corresponde localmente, vista «muy de cerca», a un espacio euclídeo, el cual está dotado de las estructuras topológica, algebraica y diferencial. Para la equivalencia de dos variedades diferenciables se utilizan los conceptos de homeomorfismo (topológico), homomorfismo (algebraico) y difeomorfismo (geométrico diferencial).
Regresando al abordaje intuitivo, la métrica permite definir un concepto para la medida de un determinado objeto en un n – espacio. Así, en la escuela elemental hablamos de la longitud de una línea, del área de una determinada superficie o del volumen de un cierto cuerpo tridimensional, como en el caso del citado volumen de una esfera. Aunque se trata de nociones bastante claras, incluidas en el discurso matemático desde los tiempos más antiguos de los que se tiene conocimiento escrito, es notable que, para evitar contradicciones extrañas, se hace necesaria toda una rama de la Matemática denominada Teoría de la Medida, en la que el concepto de medida de Lebesgue es crucial.
La no formalización de ciertos procesos, por intuitivos que parezcan, genera resultados increíbles, como el de la paradoja de Banach–Tarski, que es un teorema que afirma que una bola tridimensional, o en otro espacio, puede ser descompuesta en un número finito de partes (ocho, por ejemplo) de forma tal que las partes pueden rearreglarse para conformar otras dos bolas de igual tamaño. L a razón por la que este teorema, demostrado en 1924, se considera una paradoja, es porque contradice la intuición geométrica básica, puesto que duplicar un cuerpo, dividiéndolo en partes y removiéndolas por rotaciones, sin ningún estiramiento, curvatura, o adición de nuevos puntos, parece ser algo totalmente imposible, ya que todas las operaciones utilizadas conservan el volumen.
Sin entrar a grandes detalles, la teoría de la medida explica que la conservación del volumen es una propiedad de los conjuntos denominados medibles, y no todos los conjuntos de puntos de un espacio son conjuntos medibles. Es decir, existen conjuntos de puntos bien definidos que no son medibles, esto es, son no medibles. El secreto de la prueba es dividir un conjunto medible, como la bola, en otros que no son medibles.
Entiéndase que un conjunto no medible es un tecnicismo muy difícil de explicar acá o en literatura no profesional similar. Lo importante es que la duplicación del volumen original es posible, lo que resulta, en lo absoluto, contraintuitivo. Una de las formulaciones más sorprendentes de la paradoja dice así: «un guisante puede partirse y reensamblarse para formar el Sol». Cosas que parecen estar fuera de este mundo, pero factibles matemáticamente hablando.

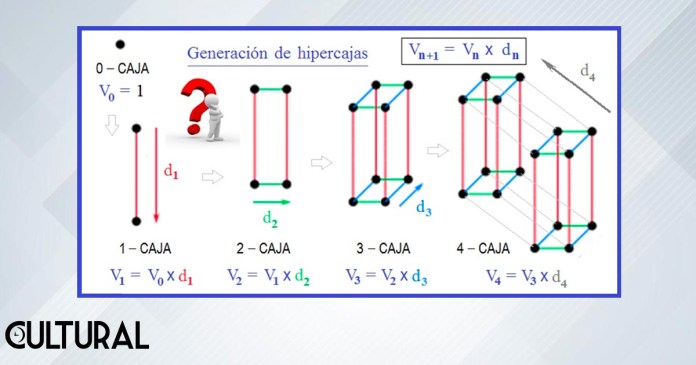
Es relevante reparar en un hecho elemental: que la medida de un objeto cualquiera en un espacio n – dimensional está basada en una medida unitaria, asignada a un polítopo de medida, o hipercubo, que es uno de los polítopos regulares existentes en cualquier espacio euclídeo. De hecho, los sólidos platónicos vienen a ser los polítopos tridimensionales, y el 3 – cubo es el cubo ordinario de nuestro mundo tangible. Para todo ello, viene a resultar fundamental revisar cómo generamos los cuerpos más sencillos en un n – espacio. Es aquí donde entra en acción la segunda parte de nuestro titular, lo relativo al desplazamiento paralelo.
En resumen, partiendo del hecho que al trasladar o desplazar ortogonalmente un cierto objeto n – dimensional en una dimensión extra, estaremos generando, automáticamente, un nuevo objeto (n +1) – dimensional. Por otro lado, podemos realizar un proceso de recurrencia respecto de la medida del tamaño, el volumen, de ciertos objetos a los que denominamos cajas n – dimensionales, o hipercajas, que será parte del titular de la continuación. El proceso, en general, se ilustra mediante los esquemas en la siguiente imagen. Esperamos describir todo esto, más detenidamente, en el artículo de seguimiento. Quedamos así, parcialmente, en cierto nivel de suspenso.
Fuente de imágenes ::
[ 1 + 2 + 4 ] Imágenes editadas por Vinicio Barrientos Carles :: O Baricentro da Mente
[ 3 + 5 ] Imágenes editadas por Vinicio Barrientos Carles :: Fuenterrebollo
[ 6 ] Imagen editada por Vinicio Barrientos Carles :: Wikipedia (prismatoid) + Wikipedia (prisma)
[ 7 ] Imagen editada por Vinicio Barrientos Carles :: Wikipedia + Blog de Emilio Silvera V.
[ 8 ] Imagen editada por Vinicio Barrientos Carles :: Correo del maestro + El País
[ 9 ] Imagen elaborada por Vinicio Barrientos Carles