Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
¡Noli turbare circulos meos!
Arquímedes de Siracusa
Llama la atención que, de manera paulatina y vertiginosa, el sistema educativo escolar tradicional, en crisis, pierde el legado de la comprensión de los hechos matemáticos más elementales. Además, resulta preocupante. Muchos y muchas se preguntan, ¿cuál es la fórmula para esto o para aquello? La voz popular lo expresa como si se tratara de artilugios misteriosos, casi mágicos. Quizá, lo más grave en este asunto de la algoritmia reductiva, es que generalmente no se tienen claros los conceptos involucrados, menos aún el objetivo perseguido, sobre cuál es el problema que se pretende resolver.
El caso del cálculo de áreas o de volúmenes de ciertas figuras o cuerpos es icónico, sirviéndonos de manera perfecta para ilustrar, ejemplificar, este distanciamiento nefasto de lo que actualmente viene a ser la formación escolar en Matemática, con lo que originalmente y de manera genuina se pretendía realizar en el Quadrivium de la Antigüedad. De hecho, para las grandes mayorías, el quehacer matemático es un asunto de conocer fórmulas y realizar cálculos. No solo lejos de la verdad, sino que, bajo esta visión algorítmica, se explica perfectamente la amenaza de la substitución de las actividades humanas por las máquinas, que son idóneas para este tipo de ejecución operacional.
Partamos del ejemplo más simple y sencillo. Muchos preguntan, o responden, casi mecánicamente, al respecto de cómo calcular el área de un triángulo rectilíneo plano. Los calificativos responden al hecho, no muy en la conciencia de todas y todos, que también pudieramos tener triángulos no planos o no rectilíneos, como los que se trazan sobre la superficie de la tierra, abarcando ciertas distancias con las cuales ya no es posible considerar que el planeta sea ciertamente plano, como usualmente consideramos en los contextos de distancias pequeñas. Pues bien, en esta arquetípica dirección se recita, como parafraseando algún tipo de oración sagrada: el área de un triángulo es la base por la altura partido dos.
La verdad, comparto, es que en múltiples oportunidades me he atrevido a preguntar sobre el porqué de tal malabarismo, al que se denomina «matemático», bajo el presupuesto de que no aparecerá una justificación que vaya más allá de: «esa es la fórmula del área de un triángulo». Como si se tratara de un dogma, un punto que tiene que ser aceptado sin discusión. El cuestionamiento o alguna reflexión no son bienvenidos. La imagen siguiente muestra, de manera elemental, el concepto de área. A su vez se ilustra cómo siempre es posible visualizar todo triángulo como la mitad de un rectángulo, de forma que su área será, cabalmente, la mitad del área del rectángulo asociado, cuadrable por definición.
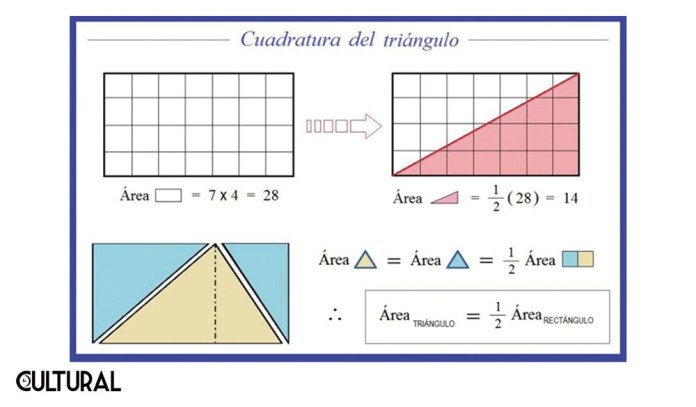
Conviene aclarar sobre el significado de este último término. Se habla de una cuadratura de una figura plana cuando es posible establecer una relación racional, es decir, del cociente de dos enteros, entre el área de la figura y un rectángulo asociado de área equivalente. Intuitivamente, esto se podrá lograr si se dispone de una cuadrícula, suficientemente adecuada, para el logro de este propósito. Cuando se trata de polígonos rectilíneos o de figuras acotadas por segmentos de recta, pareciera que lo previo, relativo al triángulo, y la triangulación, o subdivisión exhaustiva en triángulos pertinentes, no solo es factible, sino que también no tan difícil de llevar a cabo. Es decir, pareciera que un polígono rectilineo es cuadrable.
Sin embargo, al pensar en una figura no acotada por rectas, un círculo por ejemplo, el asunto pareciera elevarse a muy distintos niveles de complejidad. De hecho, cabe comentar, uno de los más famosos problemas que ocuparon a los antiguos geómetras, llegando hasta nuestros días, es el denominado problema de la cuadratura del círculo, el cual fue negativamente respondido, es decir, demostrada su imposibilidad. Fue hasta el siglo XIX que los más grandes matemáticos pudieron demostrar que no hay posible cuadratura para un círculo. Esto sucedió, indirectamente, cuando fue posible demostrar la trascendencia del número π, lo que significa que el número π no es un número algebraico, por lo que tampoco es racional, que era el quid del asunto.
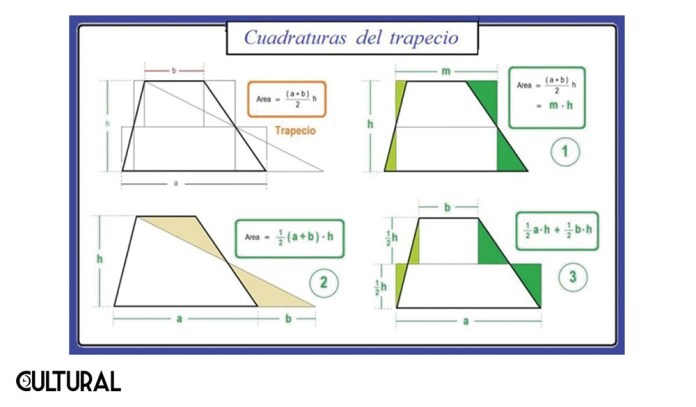
Empero, regresando a lo que sí es posible, al interés que nos ocupa en esta oportnuidad, podrán apreciarse en la imagen que sigue varias de las posibles cuadraturas del trapecio. A su vez, se puede observar que cada una interpreta, de manera diferente, la fórmula usualmente empleada para el cálculo del área de esta figura: base media por la altura. Al ser el trapecio un polígono rectilineo, cuadrilátero específicamente, se espera que el mismo fuera cuadrable. Dejamos como una inquietud para el lector y lectora que nos sigue, proporcionarle la correcta interpretación a cada uno de los trazos, líneas y movimientos de las áreas de los componentes cada una de las figuras.
La cita del inicio, del historiador y biógrafo griego Plutarco, hace referencia a la magnanimidad de la obra de uno de los científicos más importantes de la Antigüedad clásica, Arquímedes de Siracusa, quien entre tantos descubrimientos e invenciones desarrolló aportes significativos a la física, la ingeniería y la astronomía de aquel entonces, siendo revolucionario en varios sentidos. Con el correr de los siglos, la posteridad reconoció en Arquímedes uno de los matemáticos más fecundos de todos los tiempos, siendo hasta el Renacimiento y la Modernidad que tiene lugar la recuperación, reconstrucción y divulgación del legado del pensador griego, generando en los notables científicos de esta época el cuestionamiento profundo sobre sus logros.
La pregunta que cualquier persona puede hacerse es: ¿Cómo pudo Arquímedes desarrollar sus impresionantes resultados sobre cuadraturas y cubaturas, que luego demostraba rigurosamente mediante el método de exhaución? Sería hasta el advenimiento del Cálculo Infinitesimal que se le comprendería parcialmente, siendo por ello considerado precursor del Cálculo Integral, dada sus técnicas de sumación de los infinitamente pequeños. En particular, uno de sus logros es precisamente la cuadratura de la parábola, la cual aparece en un tratado con el mismo nombre, redactado en forma de carta a su amigo Dositeo.
El ensayo presenta una secuencia de veinticuatro proposiciones sobre las parábolas, anidadas y concatenadas en forma lógica, culminando con la demostración de que el área de un segmento parabólico es cabalmente 4/3 de la del triángulo inscrito, es decir 2/3 del correspondiente rectángulo que circunscribe al segmento parabólico. Este hecho, que una línea parabólica divide a un rectángulo en dos partes en relación de uno a dos, o bien de un tercio a dos tercios, será altamente significativo en sus técnicas de sumación. Si la línea que divide al rectángulo, de vértice a vértice opuesto, fuera una recta, la fracción de 1/3 se convierte a 1/2, como sucede con el área del triángulo inscrito correspondiente. Véase la imagen.
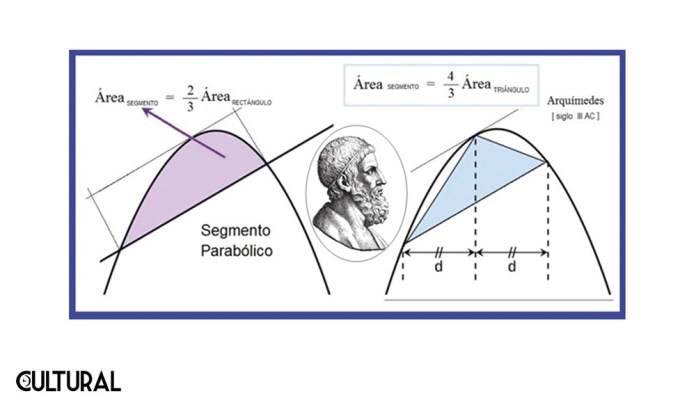
El enunciado del problema utiliza el método exhaustivo. De forma muy sintética, Arquímedes va diseccionando el área en triángulos cada vez más pequeños de tal manera que sus áreas van formando una progresión geométrica, con razón 1/4. Procede a calcular esta suma infinita obteniendo la fracción 1/3 o, equivalentemente, 4/3 si se incluye como primer término la unidad. De esta manera demostró que el área del segmento parabólico tenía esta proporción respecto al rectángulo correspondiente. En la notación contemporánea, la imagen muestra los argumentos geométricos y el cálculo algebraico correspondiente.

Respecto al genio y la profundidad intelectual de Arquímedes, el historiador, biógrafo y filósofo moralista griego Plutarco (Lucio Mestrio Plutarco de Queronea) expresa: Es imposible encontrar en toda la Geometría cuestiones más difíciles y más importantes explicadas con términos más sencillos ni más comprensibles que los teoremas de la inteligencia sobrehumana de Arquímedes. Así que, cerrando esta primera parte de la publicación, amerita agregar que la cuadratura de la parábola representó, histórica y científicamente hablando, el uso más sofisticado del método exhaustivo, también llamado de agotamiento, en las matemáticas antiguas. La imagen siguiente muestra un resumen gráfico del resultado que hemos anotado.

No fue, sino hasta el desarrollo del cálculo integral, en el siglo XVII, que las técnicas de agoamiento geométrico fueron superadas, con generalizaciones tales como la fórmula de cuadratura de Cavalieri, o el mismo principio epónimo por él formulado. Técnicas modernas del análisis numérico, como las desarrolladas por Carl Friefrich Gauss, destacarían de forma singular. Por otro lado, sobre la vida de Arquímedes se han escrito numerosas anécdotas y existen diversas leyendas, de las que no se sabe cuánto en ellas podría ser verdad y cuánto son producto de la ficción a lo largo del tiempo.
El caso es que los historiadores más serios han documentado la fama y posición que Arquímedes de Siracusa gozó en vida, haciendo ver que su reputación de científico y notable inventor no provenía de su linaje o de alguna influencia política específica, sino que era el resultado de las variadas acciones que tuvieron un impacto favorable en los pueblos, en particular en su ciudad natal donde vivió con un estatus de ciudadano magnífico. Entre estos relatos se encuentra uno que habla de una serie de inventos que posibilitaron la defensa de Siracusa por más de una década, impidiendo que los romanos pudieran ocuparla.
Por ejemplo, según la tradición, el inventor griego creó un sistema de espejos ustorios que reflejaban la luz solar, concentrando la radiación térmica consecuente sobre los barcos enemigos, con la finalidad de incendiarlos en el momento oportuno. Otro habla de la forma en que murió, y aunque existen varias versiones del hecho, se sabe que aconteció cuando la ciudad fue tomada por los ejércitos romanos, comandados por el general Marcelo.
Una de las versiones relata que cuando un soldado pretendía arrestar a Arquímedes, mientras este se encontraba absorto contemplando un diagrama matemático, el geómetra hizo caso omiso de la orden de conducción, limitándose a solicitar un poco de tiempo para resolver antes el problema en el que estaba trabajando. En esta versión, el soldado, enfurecido ante la respuesta, mató a Arquímedes con su espada, quien profirió como sus últimas palabras las citadas, en latín, en la frase inicial: «¡Nōlī turbāre circulōs meōs!» (¡No molestes a mis círculos!).
Lo que sí se encuentra mejor documentado es que el general Marcelo se mostró furioso ante la muerte de Arquímedes, debido a que lo consideraba un valioso activo científico, ante lo cual había ordenado previamente que no resultara herido. No se sabe el destino del torpe soldado que ejecutó implacablemente al polímata y pensador.
Por otro lado, pareciera existir un logro que al geómetra griego le provocó mucho orgullo y satisfacción: el del descubrimiento de la relación existente entre el volumen de la esfera, el cono y el cilindro. Arquímedes probó, en particular, que tanto el volumen como el área de la esfera son exactamente dos terceras partes del área y el volumen del cilindro que la circunscribe, respectivamente. Tanto es así que, al parecer, Arquímedes pidió que en su tumba se colocarán una escultura y unos grabados que hicieran alusión a este hecho matemático. Véase la imagen previa.
A este respecto, está documentado que, en el año 75 a. C., el orador romano Cicerón pudo visitar la tumba del erudito, constatando que sobre ella se había colocado una esfera inscrita dentro de un cilindro, conteniendo además unos diagramas con diversos resultados. En una posible próxima oportunidad estaremos tratando uno de los resultados previos para el establecimiento del volumen de una esfera, que es cabalmente el cálculo del volumen de un cono, circular recto, vinculado de manera especial y específica con otro cuerpo redondo muy conocido: el cilindro.

Como al lector seguramente le aconteció, en su momento tuvo que memorizar algunas fórmulas que le permitían el cálculo del volumen y del área de los tres cuerpos redondos presentados, en vista que el concepto de estudio que se manejaba, y que se sigue manejando, en el sistema educativo tradicional, es el de la memorización y la posible aplicación de todo cuanto el maestro pide que se aprenda.
Los pobres resultados de tales conceptos y visiones de lo que podría significar educación son visibles para todos, puesto que de todos estos esfuerzos nada o casi nada permanece, como todos y todas podemos facilmente constatar. Las escasas excepciones de las personas que aún recuerdan estas fórmulas, que en su momento fueron percibidos como extraños artilugios, no poseen una sencilla relación o explicación que justifique tales resultados, una falencia que es posible observar aún en profesionales con especialidades en temas u orientaciones de índole cuantitativa. Sirva este botón de comentario para evaluar el todo del que hacemos crítica.
A decir verdad, la simplificación a la que lleva la comprensión de los hechos matemáticos más fundamentales es la llave crucial para su estudio, su recuerdo y su perfecta utilización en aspectos de la vida cotidiana. Así, de forma particular, existen varias ideas clave con las que es posible facilitar el aprendizaje de la medida del tamaño de los distintos cuerpos y figuras geométricas. El primero es que la medida de la magnitud de un determinado cuerpo viene dado por el producto de sus dimensiones, o una determinada fracción de este consabido producto.
Así, un rectángulo es el producto de su base por su altura, de similar forma que un triángulo es la mitad de este producto. Un segmento bajo un arco de parábola es dos tercios del rectángulo que lo circunscribe, como hemos podido ver lo precedente sobre la cuadratura de la parábola. Como en estos ejemplos se trata de un área, medida en unidades cuadradas, o sea la cantidad de cuadraditos, el resultado vendrá dado por la multiplicación de dos medidas lineales. Este resultado es general y tales conceptos deberían ser parte del acervo de todos y todas aquellas personas que hemos pasado por el sistema escolar.
En tres dimensiones, el tamaño de una caja, un paralelepípedo, por ejemplo, también será el producto de su base por su altura, pero como ahora se trata de un volumen, o sea la cantidad de cubitos, la base acá será un área, en unidades cuadradas, que, multiplicada por la altura, en unidades lineales, dará como resultado una cantidad en unidades cúbicas, expresando el volumen. Así, en el cilindro, o en cualquier tipo de prisma, en tres dimensiones, la fórmula será siempre la misma, a saber: la base (en dos dimensiones) por la altura (de dimensión lineal). Esto será cierto en cualquier número de dimensiones, sin impoortar de que espacio multidimensional se trate. El fenómeno de la cuadratura es un caso particular de esta métrica en varias dimensiones.
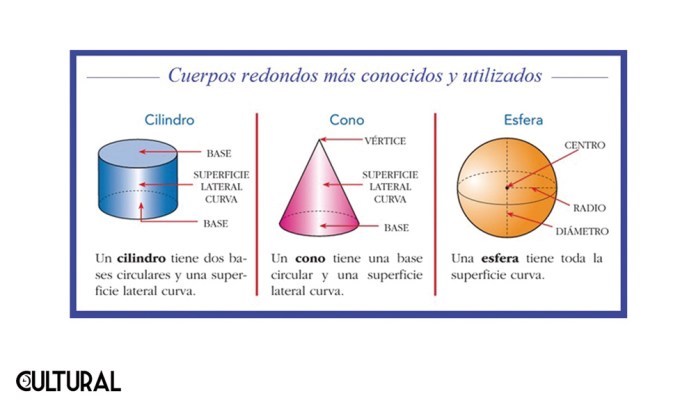
Conociendo el resultado fundamental de que el tamaño de un cuerpo es básicamente el producto de la magnitud de su base por la medida de su altura, puede uno reparar en relaciones interesantes entre ciertos cuerpos que se encuentran naturalmente vinculados entre sí, ahorrándose con esto muchas aparentes complicaciones en la metodología del aprendizaje ciego de sendos formularios que no nos dicen nada y que devienen en una colección de expresiones totalmente sin sentido.
Por ejemplo, ya citamos que una recta puede dividir a un rectángulo en dos triángulos congruentes (del mismo tamaño), a diferencia de un arco parabólico (curva de grado dos) que lo divide en dos segmentos parabólicos de tamaño un tercio y dos tercios del tamaño del rectángulo en cuestión. De similar forma, una curva cúbica (de grado tres) dividirá a un rectángulo en dos segmentos cúbicos (de grado tres) de tamaño un cuarto y tres cuartos, y así sucesivamente. En la gráfica que sigue se muestran los tres cuerpos redondos tridimensionales, con el hecho fundamental que ahora nos atañe, que es la relación entre el tamaño del cono con el del respectivo cilindro que lo circunscribe.
Si el área de un triángulo es la mitad de la del rectángulo, el volumen del cono viene a ser la tercera parte del cilindro. En este sentido, comparto, una fabulosa maestra que tuve la oportunidad de tener en mi formación primaria me hizo la observación sobre el divisor-denominador dos para dos dimensiones, y el divisor-denominador tres para tres dimensiones, como una forma comprensiva de introyectarlo y a la vez como una propiedad mnemotécnica. Recuerdo que para aquella ocasión mi recordada y apreciada maestra llevó un vasito de cono y un vaso cilíndrico de casi igual tamaño en su base, y llenando el cono de agua preguntó: ¡¿con cuántos vasitos de cono creen que se pueda llenar este cilindro de la misma altura?! Al verificarlo, la gran moraleja, que no eran dos, ¡sino tres!, los vasitos requeridos.
En suma, se dejaba la estimulante sugerencia, sobre las mentes más inquietas, que, si se tratara de un mundo con cuatro dimensiones, y tuviéramos el respectivo cuerpo similar al cono, el tamaño de este sería la cuarta parte del correspondiente cilindro. Si se investiga, podremos constatar que esta es efectivamente la situación, un poco más allá de nuestras percepciones sensibles, pero tal y como matemáticamente es factible demostrar.
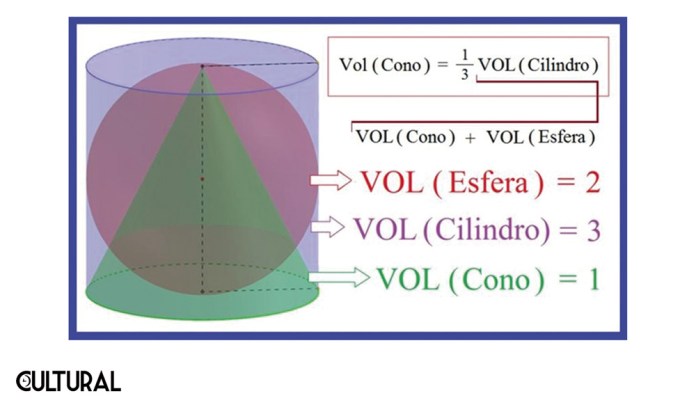
En fin, que la imagen precedente permite calcular el volumen del cono y de la esfera, siempre que apliquemos para el cilindro el principio de que su volumen viene dado por el producto de su base (un círculo: πr2) por la altura. Entonces, el cono tendrá un volumen de la tercera parte de este resultado y la esfera del doble que el respectivo cono, de manera que sumando el cono más la esfera tendremos un total equivalente al cilindro, y ese es el fundamento para el diagrama observado en la tumba del Arquímedes, mostrado en una de las imágenes previas.
Se podrá observar que, en este caso en particular, dada la relación de inscripción y circunscripción, tanto el cilindro como el cono, ambos con bases circulares y rectos (puesto que sus ejes son perpendiculares a sus bases), tienen como peculiar altura una equivalente al diámetro de la esfera, para poder coincidir de forma tangencial. Para establecer esta relación de la tercera parte, Arquímedes desarrolló con su método exhaustivo una suma infinita para determinar que la fracción apropiada para el volumen del cono es cabalmente 1/3.
Este método es semejante a como se hace ahora en un curso moderno de Cálculo Integral, como cualquier joven estudiante podrá constatar. El punto crucial para la sumación, seleccionada con la interrogante en rojo en la imagen precedente, está íntimamente conectada con el área de un segmento parabólico, problema que el matemático griego había ya resuelto previamente, y que, de alguna manera, hemos tratado de explicar en lo anterior.
Resumiendo, hemos visto la importancia que el matemático griego Arquímedes concedió al método de agotamiento o exhaución, el cual le permitiría realizar exitosamente operaciones para el cálculo con superficies y volúmenes curvos, a través del cual sentaría las bases para el posterior Cálculo Infinitesimal de la Edad Moderna, desarrollado en el siglo XVII, de manera simultánea, por el británico Isaac Newton y el alemán Gottfried Leibniz. En general, el avance de las ciencias formales siguen este desarrollo acumulativo.
En el caso particular de los cuerpos redondos, este método considera la suma (integración) de una cantidad de discos circulares (cilindros delgados de altura Δh), los cuales se van haciendo, por un lado, mayores en cantidad, y por consiguiente de un grosor cada vez más pequeño, de manera que «en el infinito» se obtendrán como totalidad las curvas y formas que se pretende medir. El caso que en esta oportunidad se plantea, el del volumen del cono, es tan solo un ejemplo de la aplicación de tal método.
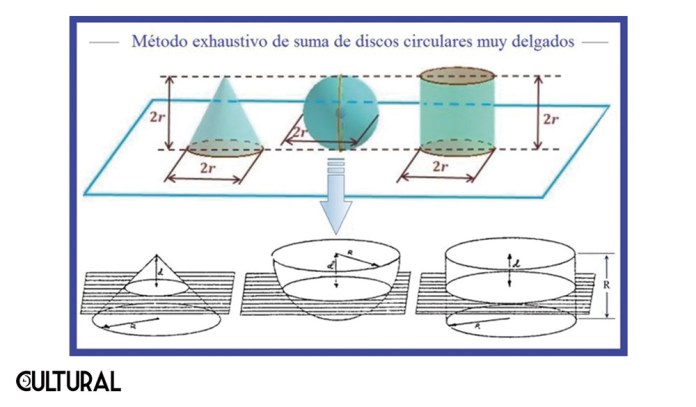
La esencia de la prueba radica en establecer que el volumen del cono será una fracción del correspondiente volumen del cilindro, fracción que se demuestra ser exactamente igual a un tercio (1/3), así: VOLCONO = 1/3 VOLCILINDRO. Otra forma de decirlo es que los correspondientes volúmenes están en relación de uno a tres (1:3). Si se parte del hecho fundamental de que el tamaño de un cuerpo tipo prisma, obtenido del desplazamiento dinámico y paralelo de una superficie o línea, es básicamente el producto de la magnitud de su base (la medida de la superficie o línea que se desplaza) por la medida de su altura (la longitud del desplazamiento efectuado), podremos vincular ambos resultados para concluir que el volumen de un cono es un tercio del área de su base (que es un círculo: π r2) por su altura.
Lo anterior, exprersado en los símbolos estándar, queda así: VOLCONO = 1/3 Bh = 1/3 π r2 h, que es la fórmula que seguramente aparecerá en los manuales de los que hemos hablado anteriormente. Como podremos deducir en artículo próximo, el volumen de la esfera corresponde al doble del cono correspondiente, encontrándose entonces los tres cuerpos en la proporción dada por 1:2:3, como se puede apreciar en la imagen que a continuación se muestra.
Para determinar la suma de una cantidad inmensa (¿infinita?) de delgadísimos discos (infinitesimales), tipo láminas, es necesaria una expresión algebraica que podamos manipular en el límite, es decir, cuando se imagina que tomamos un número de tales láminas que crece sin cota. El punto crucial para la sumación, seleccionada con la interrogante en rojo, en la imagen que sigue, estará íntimamente conectada con el área de un segmento parabólico, como se indica. Para Arquímedes esto resultó notable, y muy estimulante, pues él fue el primero que realizó el cálculo del área de un segmento parabólico, como previamente ilustramos en el artículo sobre la cuadratura de la parábola.
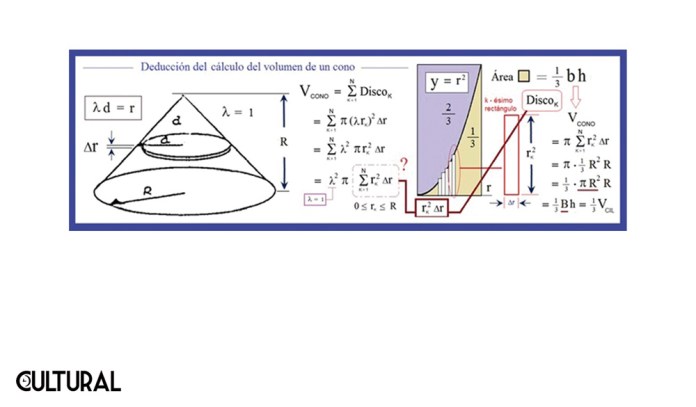
En la Matemática de ayer y hoy es clásica y característica la traslación de una cierta área, disciplina o problema a otro que no evidencia la conexión de una forma inmediata. Así, un problema determinado se ve transformado en otro, de manera que, al resolver este segundo, el primero queda total o parcialmente resuelto. En este caso que estamos tratando, se observa cómo calcular el volumen de un cono (circular recto, de altura r, el radio de la base), se transforma en otro, que es el de calcular el área de un segmento parabólico, o bien, en lenguaje más analítico y menos geométrico, como suele usarse hoy en día, se transforma en el cálculo bajo una curva de segundo grado, un arco de parábola.
En nuestro ejemplo, cada lámina circular tiene área π r2, y se trata de sumar (integrar) todas estas áreas a lo largo de una altura R. Esta suma de π r2 se convertirá en el área amarillo marrón que se muestra en la imagen previa, que justamente Arquímedes había calculado previamente y en la cual aparece la esperada fracción 1/3.
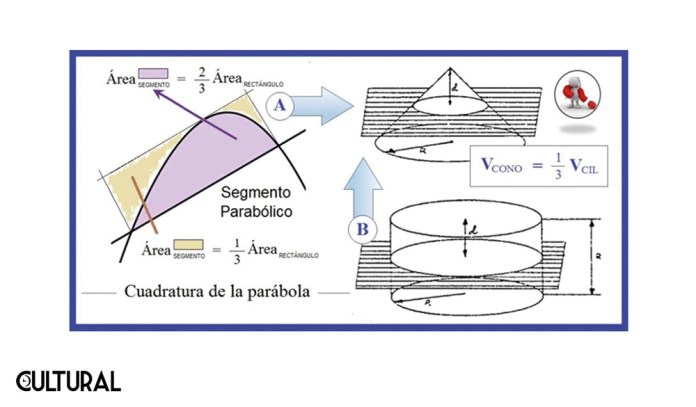
Recordaremos que, para el caso del tamaño de un triángulo, se usa la fracción un medio (½). Mencionamos el análogo para un cono, en el que lo correcto será utilizar la fracción un tercio (1/3). La correspondencia es clara y ahora generalizable. Usando el problema homólogo del cálculo bajo un área, se tiene que, bajo una recta, una curva de grado 1, tendremos una fracción de un medio (1/2), mientras que para el volumen del cono ha resultado el área bajo una parábola, una curva de grado 2, y de ahí que la fracción resultante sea de un tercio (1/3).
De esta guisa, uno podría esperar que bajo una curva de grado 3 se obtendrá un área equivalente a una fracción de un cuarto (1/4) del rectángulo que la circunscribe, y así sucesivamente para curvas de una grado mayor, que es justamente lo que enuncia la denominada fórmula de cuadratura de Cavalieri, denominación epónima por el matemático italiano Bonaventura Cavalieri, discípulo de Galileo Galilei, quien la planteara explícitamente por vez primera en el siglo XVII, muchos siglos después de su precursor, el geómetra de Siracusa que en esta ocasión estamos elogiando, como indica nuestro titular.
El término cuadratura es un término tradicional utilizado para el área, como hemos explicado, pero en general puede referirse a la suma exhaustiva a lo largo de un cuerpo curvo, lo que a su vez puede reproducir el tamaño de un cierto cuerpo. Un caso particular de una curva de grado n ha sido el de la parábola; en términos generales, una integral se podrá interpretar geométricamente como el área bajo la curva en cuestión, y esto nuevamente es un logro arquimediano plasmado en el tratado enviado a Dositeo en la forma epistolar.
A manera de resumen, aunque han quedado varios cabos sueltos, hemos comprendido que las fracciones un medio y un tercio, para las dos o tres dimensiones, en el cálculo del tamaño de un triángulo (área) y un cono o pirámide (volumen) provienen de la consideración de una suma infinitesimal de una recta o una parábola. En este escenario de abstracción, con miras a una plausible generalización, podría pensarse que el tamaño de un cono más general n-dimensional, en un espacio n-dimensional, podría obtenerse de una manera similar, análoga. Esto, en efecto, es factible, como posiblemente podamos abordar en otra oportunidad.
Como apreciamos, de varias maneras, con esta exploración, estaremos abriéndonos camino a otras curiosidades que, aparte de interesantes, podrán parecernos sorprendentes. Así, podremos ir descubriendo, sin prisas, pero sin pausas, las maravillosas realidades del mundo abstracto de la Matemática. Por ahora, nos quedamos con estas del día de hoy.
Fuente de imágenes:








