Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
La Matemática es la reina de las ciencias, y la Aritmética es la reina de la Matemática.
Carl Friedrich Gauss
Hace casi ya seis años, antes de los tiempos de la pandemia, escribimos un artículo titulado «Dos más dos, no siempre son cuatro», en el cual colocábamos unos ejemplos bajo los cuales el consabido resultado de 2 + 2 = 4 no se cumplía. Lo anotábamos como ilustración de dos hechos importantes. El primero, relacionado con que la Matemática, como disciplina del saber y del conocimiento, no se refiere a un sistema o modelo único, sino que trata de diversos sistemas formales, por lo que no debe asumirse ni restringirse al conocimiento de lo que aprendemos en la escuela elemental, en este caso de los números naturales, en donde, en efecto, se tiene que «dos más dos son cuatro»: 2 + 2 = 4.
El segundo, no menos importante, exhibe que la Matemática no trata sobre verdades absolutas, como la mayoría de las personas piensan, es decir, que no trata con cuestiones inamovibles o reciamente establecidas. Por el contrario, la Matemática y los sistemas formales que la conforman refieren a asuntos que en el fondo son muy relativos, al menos en su momento de partida, pues dependen directamente de las axiomáticas y de las reglas, por así decirlo, que se consideran verdaderas en un determinado modelo o sistema formal.
En este sentido, para ejemplificar las nociones, suele escucharse decir: «las matemáticas no fallan». Sin embargo, este tipo de frases, absolutistas, son habitualmente peligrosas fuentes de error, en vista que se ignoran los alcances semánticos involucrados, y en diversidad de casos, derivan en los límites de aplicación de la ciencia. En Matemática, se repite, las cosas serán tal y como las reglas en los sistemas lo dicten. Así, más que de verdades empíricas inobjetables, se trata de verdades relativas, es decir, establecidas por convención o por conveniencia. La fortaleza de la disciplina proviene del hecho de que, si tales o cuales situaciones se asumen, entonces, necesariamente, por fuerza lógica, otras tendrán que darse, indefectiblemente. De esto tratan los teoremas.
En primera instancia, debemos reconocer que hoy en día resulta muy difícil imaginar un ámbito del desempeño humano en el cual las teorías y modelos matemáticos no sean particularmente importantes. Un segundo estereotipo es el referido a la conceptualización de la actividad matemática como algo «circunscrito a la realización de operaciones, cálculos y demás aplicaciones de reglas mecánicas», extraídas quién sabe cómo, ni de dónde. En pocas palabras, una acepción que reduce a las matemáticas a procesos de tipo algorítmico: una colección de normativas para realizar cálculos de manera eficaz. De esto ya hemos conversado en «Operaciones y razonamiento».
Pues bien, en seguimiento del titular de esta ocasión, y en vista de que la connotación numérica es la más conocida, en lo que a el quehacer matemático se refiere, se reconsidera la frase tan popular que dice: tan claro como que dos más dos son cuatro, o en símbolos, «2 + 2 = 4». Con la intencionalidad de ilustrar cómo son posibles distintas interpretaciones ante un mismo cuestionamiento, según sean los sistemas formales considerados, se citan a continuación cuatro ejemplos sencillos que copiamos la vez anterior, orientados a modificar el preconcepto de respuesta única conforme un sistema matemático absoluto. En efecto, es posible escribir que:
2 + 2 = 1, en una aritmética de módulo 3, para lo cual convendrá imaginarse un reloj de aguja con únicamente tres marcas. La expresión indica que, si la aguja se posiciona en la marca «2» y se avanzan dos unidades, se llegará a la marca «1».
2 + 2 = 11, en la aritmética usual de los números naturales, pero escribiendo estos en el sistema de base tres. En este sistema posicional, cada posición representa un valor tres veces mayor que el precedente, de igual manera que en el sistema de base diez, cada posición representa un valor diez veces más grande que el anterior. Así, la combinación de guarismos «11», en el sistema de numeración de base tres, es el numeral que representa al número cuatro, pues equivale a una unidad de valor uno y otra que vale tres.
2 + 2 = 22, en donde el símbolo «+» representa la conocida operación de concatenación, y habitualmente leída como «dos y dos son veintidós». Esta operación de concatenación es básica y fundamental en el estudio de la Computación.
2 + 2 ≈ 6, en una aritmética intervalar de techo. Quizá esto provoque extrañeza, pero es la lógica que se aplica cuando se debe pagar en un almacén después de haber comprado una prenda de «dos y pico» de valor, junto con otro artículo, también de valor «dos y pico». Claramente, tendrás que preparar una disponibilidad de seis para el pago del posible monto total. Esto es, para el pago de dos artículos que valen Q 2 con algo, tendrás que entregar Q 6. Esta es una operación que solemos aplicar con frecuencia.
En esta oportunidad, nos ocuparemos de uno de estos sistemas que en la ocasión previa citamos como uno de aquellos en los que las expresiones estándar tienen otros valores distintos de los que usualmente utilizamos, y veremos que tales resultados pueden ser aplicados en nuestro mundo cotidiano. De hecho, descubriremos que nos son más familiares de lo que podríamos pensar. Estamos hablando de la denominada aritmética modular. En nuestra exposición, para variar un poco la modalidad verbal, que usualmente utilizamos, estaremos ahora recurriendo a imágenes, al menos un poco más de lo acostumbrado.
No obstante, antes de presentar el sistema de la aritmética modular, o matemática del reloj, y sus potenciales usos, podemos reparar que en cualquiera de los entornos coloquiales en los que hace su aparición el concepto de «número», que por cierto es polisémico, resulta conveniente distinguir dos connotaciones fundamentales en su aplicación. Estos dos usos suelen contraponerse, porque corresponden a diferentes niveles de medición, siendo uno referido a los conteos, de resultado discreto (sea ordinal o cardinal), es decir, de números con valores necesariamente enteros, sin fraccionamientos, y el otro, referido a una medición propiamente dicha, que implica el uso de cantidades que aceptan subdivisión, continuas, por lo cual serán siempre, necesariamente, de tipo aproximado.
Presentando un ejemplo, nótese que cuando usamos el número «siete», podemos distinguir las dos modalidades, así: la primera, en la frase «se compraron siete manzanas», mientras que la segunda en «la tabla mide 7 pies de largo». Obsérvese que, en el primer caso, se trata necesariamente de un número natural, siempre entero y positivo, que como tal no admite fraccionamientos. Por otro lado, se verá que en el segundo caso se habla de un número racional, que sí admite división y fraccionamientos, por lo que se tratará de un valor aproximado del valor real, siendo esta una aproximación con un cierto grado de significancia. Véase con detenimiento el esquema de la siguiente imagen.

Se afirma que el primer caso se refiere a una cantidad discreta, medida por una variable discreta, que arroja un número natural; mientras que, en el segundo, se trata de una cantidad continua, medida por una variable continua, que se será determinada por medio de un número racional, es decir, de naturaleza fraccionaria. También obsérvese que, para el caso discreto, dada su naturaleza, se podría obtener un valor exacto del conteo, cuestión básicamente imposible para el segundo, en el cual resultará crucial la consideración de la mencionada significancia de los resultados de un proceso de medición, incluyendo aquí el tema de variables, instrumentos y de la específica metodología métrica empleada.
La aritmética modular, o cálculo con clases residuales, se refiere a un sistema que trata con clases de equivalencia de números enteros, denominadas clases de congruencia. Así, este sistema trata con números naturales, que refieren a cantidades discretas; por otro lado, el sistema contiene una cantidad finita de elementos, a diferencia de los números naturales que representan el conjunto infinito más sencillo.
Formalmente, estas clases de equivalencia, o clases residuales, fueron tratadas por Carl Friedrich Gauss cuando él era, apenas, un adolescente, sistematizando la mayoría de sus resultados en su obra magna Disquisitiones arithmeticae, redactada en 1798, a sus tempranos veintiún años de edad. Esta obra sentó las bases fundamentales para el posterior desarrollo de la moderna teoría de números, una de las áreas más interesantes y difíciles de la Matemática de todos los tiempos.
Aterrizando en el tópico modular, sabemos que todas y todos estamos relacionados con la clasificación de los números naturales en pares y nones, los impares. Tal separación representa una partición de todo el conjunto de los números naturales, en el sentido de que todo número natural es, de forma excluyente, o par o impar, siendo los primeros aquellos que tienen una mitad entera, es decir, que son el doble de otro número natural.
Es así como, cuando aprendemos a contar, nos percatamos que la sucesión de naturales sigue la secuencia par-impar de forma indefinida. Pronto descubrimos algunas reglas, tales como que, si sumamos un número par con otro número par, tendremos necesariamente, por fuerza, otro número par. Este es, de hecho, un sencillo teorema.
Quizá no podamos hacer una demostración formal, pero sabemos con toda certeza que la adición de un número impar más otro número impar nos dará por resultado un número par. Si a estas dos partes, o clases, les damos un nombre, podremos resumir nuestras reglas de operación en unas tablas que describen esta aritmética. Podemos llamar 0 a la clase de los números pares, y 1 a la clase de los números impares. En la imagen que sigue, veremos las reglas que todos fácilmente podríamos aceptar, de una forma casi empírica, con base en nuestra experiencia con los números naturales y sus operaciones.
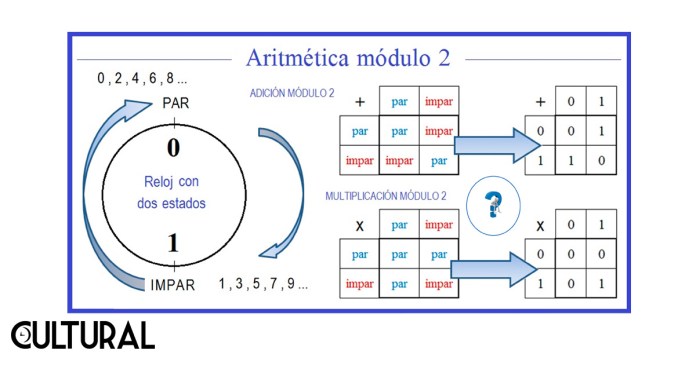
Se observará que hemos colocado un círculo, puesto que sin mucha dificultad podremos ver que este caso de pares-impares, o módulo 2, podrá ser generalizado a un número mayor de divisiones en el círculo previamente mostrado en la imagen. De hecho, algunas veces, a la aritmética modular que estamos presentando se le llama, sugerentemente, aritmética del reloj, ya que los números conformarán un reloj circular estándar al que le «dan la vuelta», tras alcanzar cierto valor, que es justamente el parámetro al que se le llama el módulo del sistema.
La imagen previa corresponde al sistema de módulo 2. Nótese que en este sistema solo existen dos elementos, a saber: 0, pares y 1, impares. Las reglas aritméticas en este reloj se muestran en la derecha. Aquí tendremos, por ejemplo, que: 1 + 1 = 0, pues impar sumado con otro impar, será par, necesariamente. Puede verificarse la tabla presentada.
Podemos intentar generalizar esta idea al caso de cuando el módulo es 3. En este caso tenemos como elementos principales, o de base, aquellos números naturales que pueden ser divididos dentro de 3 de una manera exacta, es decir, los múltiplos de tres, en la secuencia, por todas y todos conocida: 0, 3, 6, 9, 12, y así sucesivamente, de tres en tres. Para cualquier múltiplo de tres, como es divisible exactamente por tres, será posible representarlo por la fórmula 3n, donde n es un número natural. De manera inversa, cualquier resultado en la fórmula 3n dará como resultado un múltiplo de tres.
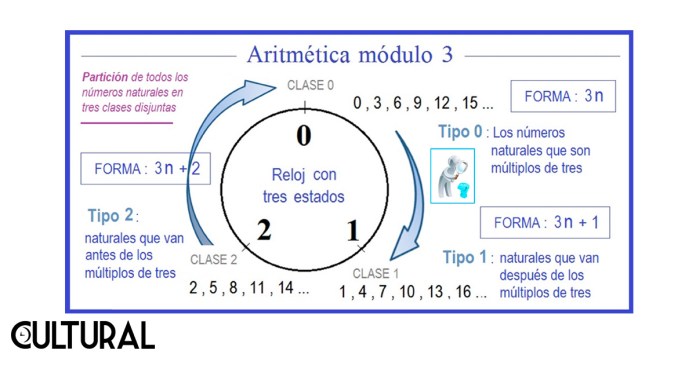
Así, por ejemplo, sabemos que 21 es múltiplo de 3, pues 21 = 3 (7) = 3 n, con n = 7. También, sabremos que el número 51 será un múltiplo de 3 si y solo si podemos escribirlo en la forma 3n, donde n es algún número natural. Este es, justamente, el caso, pues podemos verificar que 51 = 3(17), de donde 51 es también múltiplo de 3. Ya habiéndonos percatado de esta definición y del hecho que, en la secuencia de números naturales, los múltiplos de tres van cabalmente de tres en tres, podremos proceder a imaginar un círculo que contiene tres posiciones.
En este reloj de tres marcas, podremos colocar todos los números naturales en una espiral infinita. Lo fabuloso será descubrir que este artefacto genera una clasificación en tres tipos de números naturales, como se muestra en la imagen previa a este párrafo. En la marca 0 caen todos lo múltiplos de tres, así como en la marca 1 caerán todos los que siguen a un múltiplo de 3. Finalmente, en la marca 2 vienen a estar todos aquellos números que se encuentra antes de los múltiplos de 3. Revísese y se verá que cualquier número natural es del tipo 0, o del tipo 1, o del tipo 2.
Lo sorprendente es que podríamos imaginar ahora un conjunto abstracto formado por tres elementos que se relacionan mediante las operaciones de adición y multiplicación, obteniendo un sistema matemático independiente, coherente y ciertamente útil. Lo que afirman las tablas de operación en la imagen que sigue es la forma en que estos tres objetos pueden ser combinados, de forma lógica y consistente. Así, al establecer que 2 + 2 = 1 estamos aseverando que la clase identificada por 2 sumada con la misma clase 2 nos dará por resultado la clase 1. De esto y más estaremos ampliando en lo que sigue, pero, por ahora, quizá jugar un poco con el modelo, identificando varios números en las marcas respectivas.

Recapitulando hasta acá, empezamos realizando un recordatorio al respecto del uso que con frecuencia le damos a los números, distinguiendo las cantidades discretas de las continuas. Lo discreto refiere a los conteos de cosas enteras, no fraccionables, y lo continuo refiere a las mediciones, de objetos o cosas que sí se pueden fraccionar, de alguna manera. Presentamos unos primeros sistemas matemáticos, discretos, que utilizan números, pero no en el sentido usual que les otorgamos en nuestras operaciones aritméticas cotidianas, de forma tal que se presentan hechos que nos pueden parecer incorrectos, como cuando se afirma que 2 + 2 = 1.
Todo esto, en contra del estereotipo de que el quehacer matemático es mecánico y cerrado, no dando lugar a arbitrariedad alguna. A decir verdad, insistimos que, cabalmente, la Matemática es la disciplina racional de naturaleza relativa, por excelencia, pues cada afirmación o verdad aceptada o demostrada en un determinado modelo o sistema, dependerá de las premisas o fundamentos sobre los que se construye el edificio deductivo referido a este modelo o sistema, todo esto en un sentido formal, pues las aplicaciones tienen otras consideraciones de importancia.
Así, retornando a los ejemplos específicos de la denominada aritmética modular, pudimos observar, de manera rápida, algo del funcionamiento de estos sistemas numéricos, presentando dos maneras de abordar su construcción. Para empezar, nadie tiene duda sobre lo que significa un par o un impar, porque estamos familiarizados con los números naturales que tienen una mitad exacta, los pares, y los que no pueden ser partidos en dos sin dejar residuo, los impares. Se pidió algo de actividad lúdica, para observar la dinámica entre suma y producto entre pares e impares.
De hecho, en nuestro sistema decimal de numeración, reconocemos el tipo de paridad por la cifra en que termina el número. Este caso, de pares e impares, es el correspondiente a las congruencias módulo 2, en donde se generan, cabalmente, dos clases residuales. La siguiente imagen muestra las dos formas fundamentales de ver el fenómeno y el significado de la operación de módulo, en estos casos particulares del módulo 2 y del módulo 3.
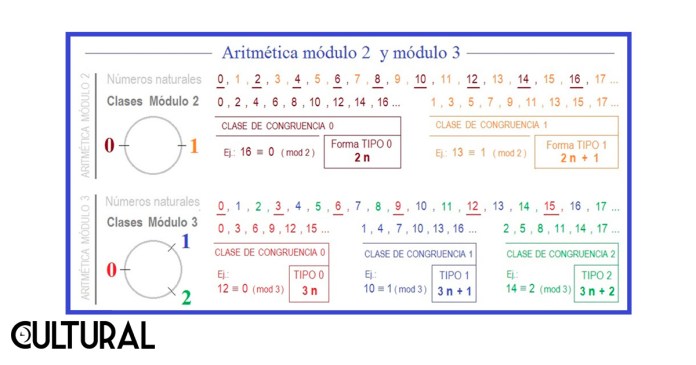
Así, vemos cómo el conjunto de todos los números naturales, y realmente de todos los enteros, puede ser partido en una cierta cantidad de subconjuntos, los cuales son disjuntos y exhaustivos. Estos subconjuntos son las denominadas clases de congruencia módulo k, donde k será el número de clases en que se parten los naturales. Por otro lado, se establecen sendos objetos matemáticos, estas clases de congruencia, los cuales pueden ser operados entre sí, como si se tratará de «números» en sí mismos, porque estas operaciones pueden ser identificadas como adición, sumando clases, y multiplicación, obteniendo el producto de clases.
Al final, obtenemos un sistema finito conformado por k objetos, que, aunque son identificados con los mismos signos de nuestros conocidos números naturales (0, 1 , 2 , 3, …), nos percatamos que se trata de nuevos objetos, ciertamente diferentes. Por otro lado, estos nuevos objetos son graficados en un reloj de k marcas, similares a nuestro convencional reloj horario, de 12 marcas, y responden a una lógica aritmética similar.
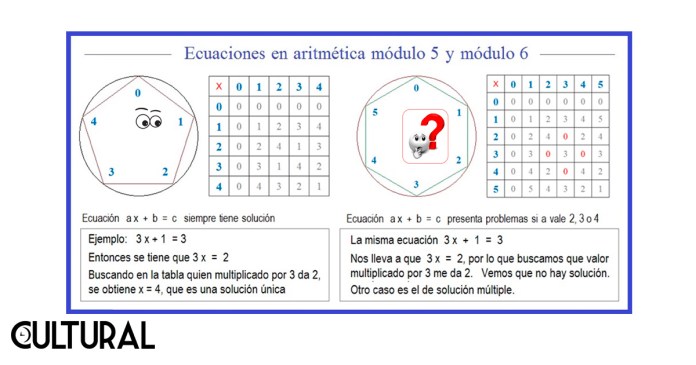
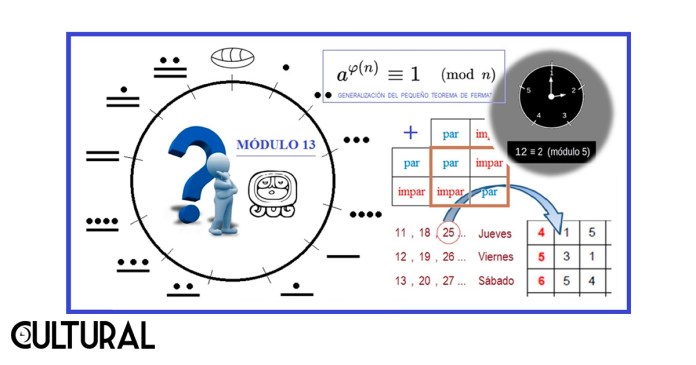
Estamos acostumbrados al uso del reloj análogo, e original círculo con doce marcas, de manera que, si pasan tres horas después de las 11 de la mañana, comprendemos que ahora son las 2 de la tarde. Si a una persona, inclusive con reloj digital, en el modelo de doce horas, le preguntamos, «mira, ¿qué hora será tres horas después de las 11 am?», sabemos que nos responderá: «serán las 2 pm». Es decir, en otras palabras, estamos familiarizados con lo siguiente: 11 + 3 = 2 (mod 12). De similar forma podríamos operar con otros relojes que tuvieran un número k arbitrario de marcas. Véanse y analícense, en la imagen que sigue, las operaciones de adición y multiplicación en módulo 3 y módulo 5, es decir, para los relojes con 3 y con 5 marcas, respectivamente.

Cuando anotamos que 2 + 2 = 1 (mod 3), se afirma que cualquier número tipo 2, sumado con cualquier otro número tipo 2, siempre en el módulo 3, nos dará como resultado un número que necesariamente será del tipo 1, en el módulo 3, es decir que estará contenido en la clase de congruencia 1, módulo 3. Invitamos a la lectora y al lector a verificar este hecho, con diversidad de ejemplos.
Únicamente, procedamos acá a uno de estos ejemplos, en el reloj de tres marcas, es decir, en la aritmética de módulo 3. Tómese el 29, que es un número tipo 2, en módulo 3, lo cual se escribe 29 ≡ 2 (mod 3), y se lee diciendo que 29 es congruente con 2 en el módulo 3. Por otro lado, tómese otro similar, el 44 (44 ≡ 2 : mod 3), de forma que al sumar 29 con 44 tendremos por resultado un número que será de tipo 1, es decir, congruente con 1, módulo 3. Vemos, verificando, que: 29 + 44 = 73 ≡ 1 (mod 3). La justificación la encontraremos en el hecho aritmético que establece: 2 + 2 = 1 (mod 3). Cualquier número tipo 2, sumado con otro número tipo 2, nos dará por resultado un número tipo 1. Eso es lo que se dice en la congruencia: 2 + 2 = 1 (mod 3).
Análogamente a este ejercicio que hemos efectuado, rápidamente, con un reloj de tres marcas, se pueden realizar otros, con relojes que tengan otro número de marcas. No obstante, resulta oportuno hacer mención que la escogencia del módulo es un hecho fundamental, pues redundará en las propiedades del sistema que se construye. En efecto, si el módulo k posee divisores, esto es, si se trata de un número compuesto, no se tendrá ciertas propiedades que resultan convenientes, matemáticamente hablando.
Este hecho matemático se puede apreciar en la imagen siguiente, en donde se está comparando el funcionamiento de los relojes con cinco y seis divisiones. Si el módulo no tiene divisores propios, es decir, si k es un número primo, podremos ver que la estructura algebraica generada poseerá las propiedades de un campo (o cuerpo), íntimamente ligadas con el concepto de número, como trataremos posteriormente, en una próxima ocasión. En la imagen que sigue, se ilustra esta importante propiedad, pues el número 5 es primo, no tiene divisores, mientras que el 6 sí los tiene. Esto deriva en algunas problemáticas para la aplicación de la aritmética módulo 6, en asuntos cotidianos, como podrá apreciarse en las tablas correspondientes a esa aritmética modular.
Veamos ahora, a vuelo de ave, una aplicación con el módulo siete, vinculado con un sistema que nos es totalmente familiar: los siete días de la semana. Específicamente, en la imagen siguiente se plantea un problema sencillo, que se resuelve usando la aritmética módulo 7. Se trata de 25 actividades secuenciales de 9 días de duración cada una, lo que hace un total de 225 días (225 = 25 x 9). Si deseo que se termine el total de las actividades en un día domingo, me pregunto: ¿qué día de la semana debo iniciar? Tenemos: 25 ≡ 4 (mod 7) y 9 ≡ 2 (mod 7), por lo que el proyecto durará 2 x 4 ≡ 1 (mod 7), lo cual se realiza en una calculadora científica estándar. La ecuación a resolver es: 2 x 4 + X = 7 ⇒ 1 + X = 7 ⇒ X = 6. De aquí que la solución venga dada por: «debe iniciarse un día sábado».

Mencionamos que estos sistemas matemáticos fueron estudiados ampliamente por Carl Friedrich Gauss a muy temprana edad, apuntando los teoremas fundamentales en su magnum opus, Disquisitiones arithmeticae. Sin embargo, mucho antes de la modernidad occidental, estos conocimientos fueron aplicados en otras culturas, y en este sentido, cabe hacer especial mención de la cultura maya, pues la matematización subyacente en el desarrollo de sus complejos sistemas de calendario exhibe un profundo conocimiento de la aritmética modular.
Uno de sus calendarios, el tzolkin, utiliza una división conformada por dos ruedas cíclicas, una de trece días y otra de veinte, generando un período de 260. De lo apuntado acá, podrá apreciarse la escogencia del número 13, que es primo, en contraposición al 12, que en Occidente se heredó de la cultura babilónica. Esto demuestra que los mayas tenían un mejor conocimiento matemático de estos sistemas aritmético modulares, en parte por su concepción cíclica del cosmos, como puede apreciarse en su calendario y en sus estudios astronómicos.
Por ello, seguramente que todo esto es tópico al que deberemos regresar, en futura oportunidad, extendiéndonos un poco más, quizá más lento, recorriendo y compartiendo curiosidades que en estos maravillosos caminos de la aritmética modular pueden encontrarse Por ahora, nuestra expectativa ha sido la de haber logrado despertar el necesario interés para esta continuidad.
Fuente de imágenes:
[ 1 a 9] Imágenes elaboradas por: Vinicio Barrientos Carles








