La cortesía de un número

Vinicio Barrientos Carles

Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior.   Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar.   Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.

 

La esencia de las matemáticas no es hacer las cosas simples complicadas, sino hacer las cosas complicadas simples.    

Stanley Gudder

En las distintas publicaciones que he venido haciendo de hace un tiempo a acá, hemos comentado, en más de una oportunidad, que la Matemática no es solo cuestión de números. Se trata de estructuras formales, puramente ideales o existentes en el mundo sensible, que obedecen algunas reglas o relaciones que determinan el comportamiento de los objetos en tales estructuras, los cuales muestran ciertos patrones, de forma tal que cuando logramos abstraer estas relaciones a las que los objetos matemáticos responden, podemos establecer un sistema formal, de naturaleza deductiva, que nos permitirá probar teoremas, verdades de fuerza lógica que necesariamente se cumplirán en estos sistemas, denominados sistemas o modelos matemáticos.

Los procesos lógicos intervinientes en la construcción, deducción y demostración (derivación de nuevas proposiciones válidas) son fundamentales, constituyéndose en los pilares sobre los cuales los distintos edificios matemáticos descansan y se erigen, conformando en su conjunto las teorías y las subdisciplinas de esta ciencia. Es importante, a diferencia de lo que suele pensarse, recalcar lo que el profesor Stan Gudder nos dice en la frase inicial, pues es característica universal de los sistemas matemáticos, no solo la abstracción en la que se mueven, que implica una simplificación de los contextos, sino la esencial sencillez con la que se trabaja, conservando únicamente los elementos fundamentales de las ideas a tratar, concluyendo todo ello en una belleza sin par.

Aunque los objetos matemáticos no son exclusivamente de tipo numérico, lo cierto es que posiblemente sean estos los más antiguos, sobre los que se han ido construyendo otros conceptos, en torno del espacio, las formas y los diferentes tipos de relación.   En este sentido, en mi columna Quadrivium, hemos ido abriendo, paulatinamente, ventanas a nuevos espacios, con otro tipo de objetos matemáticos, un tanto más desconocido.   Empero, los números suelen representar un lugar común, por la familiaridad que tenemos con ellos, porque son incluidos en la formación matemática elemental y porque pueden llegar a ser muy divertidos, al realizar con ellos una serie de entretenimientos aritméticos.

También, cabe mencionar, que quienes nos leen han manifestado una especial predilección por las temáticas numéricas, lo cual comprendemos como consecuencia del énfasis que el sistema educativo escolar ha colocado en ello, a punto tal, que es frecuente concebir la habilidad o talento matemático como el relacionado con cierta facilidad para operar números, esto es, a la capacidad exclusivamente aritmética.   Empero, es importante subrayar que, en general, esto no es así, pues hay matemáticos y matemáticas notables cuya habilidad aritmética no es superior al estándar, es decir, siendo a veces inferior al rendimiento aritmético promedio.   Sobre el talento matemático, escribíamos recientemente, en estos suplementos culturales LaHora,  al respecto de las Olimpíadas matemáticas.

No obstante, en esta oportunidad, estamos abordando un tema que va en la dirección de los números, como bien indica el título del artículo, esperando que sea de agrado, por su fácil comprensión y porque puede resultar en una amena diversión.   A su vez, la temática se encuentra vinculada con la denominada matemática recreativa, una interesante área, conformada por actividades de tipo lúdico, juegos, que involucran el desarrollo de competencias de tipo lógico y matemático.   Sobre la matemática recreativa, en Wikipedia puede leerse lo siguiente:

La matemática recreativa es un área de las matemáticas que se concentra en la obtención de resultados acerca de actividades lúdicas, y también la que se dedica a difundir o divulgar de manera entretenida y motivadora los conocimientos, temas o problemas de las matemáticas.   El concepto de matemática recreativa es tan viejo como lo son los juegos en los que interviene la lógica o el cálculo de algún modo.

Cabe mencionar que existe una lista no pequeña de difusores y profesionales que se han dedicado a promover el quehacer matemático mediante el cultivo, la divulgación, de las matemáticas recreativas.   En especial se menciona a Martin Gardner, con libros como El ahorcamiento inesperado y otros entretenimientos matemáticos, y Nuevos pasatiempos matemáticos.   También se ha leído mucho a Yákov Perelmán, quien publicó distintos libros sobre aritmética, geometría, álgebra, física y astronomía recreativas.     En nuestro caso, estaremos dentro del campo de la aritmética recreativa, pues, como reza, estaremos hablando de la cortesía de los números.

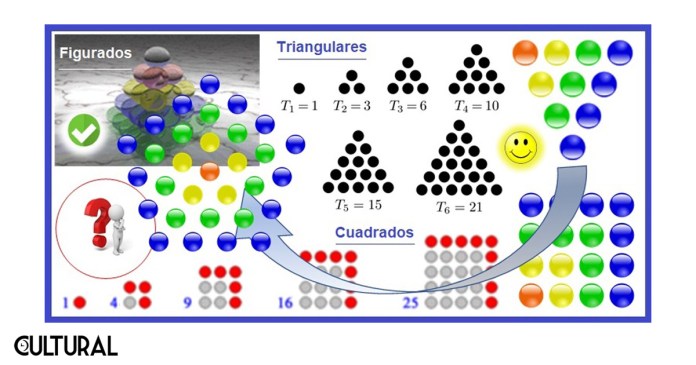
Para introducirnos en el tema, conviene empezar viendo los números figurados, los cuales se corresponden con una determinada figura.   Para ello, es pertinente recordar a los números cuadrados.   Sabemos que algunos números naturales son cuadrados, esto es, de la forma n².   Un primer ejemplo es el 9, que sabemos que es cuadrado pues se tiene que 9 = 3².   En este rumbo, digamos que los números figurados son aquellos que pueden disponerse en una estructura que tenga una forma geométrica determinada.   Por ejemplo, algunos números tomarán la forma de un cuadrado, de un triángulo, de un rectángulo, de una escalera, etcétera.

En este sentido, en un artículo previo presentamos los números triangulares, que son aquellos que cabalmente resultan de un arreglo en forma triangular.  Explicamos que, para construirse, se coloca una secuencia de filas de fichas, por ejemplo, aunque bien pueden ser usados frijolitos, piedrecitas o cualquier otro objeto homogéneo.   Lo importante es cada fila tenga una unidad más que la anterior, empezando por una fila con un objeto únicamente.

Así, por ejemplo, al colocar cuatro filas, tendremos en total 1 + 2 + 3 + 4 = 10 objetos, de manera que T₄ = 10 es un número triangular.   Colocas una fila con 1 ficha, la siguiente con 2 fichas, la tercera con 3 fichas y la última con 4 fichas.   Obtienes así una conformación denominada tetraktys, que tendrá en total 10 fichas.   Con esta figura demuestras que 10 es un número triangular, pues puedes construir un triángulo con exactamente 10 fichas.   El lector y la lectora pueden construir otros números triangulares, los cuales responden a la fórmula ½ n (n+1), donde n es el número de filas, o bien, si se quiere, el número de objetos de la base.

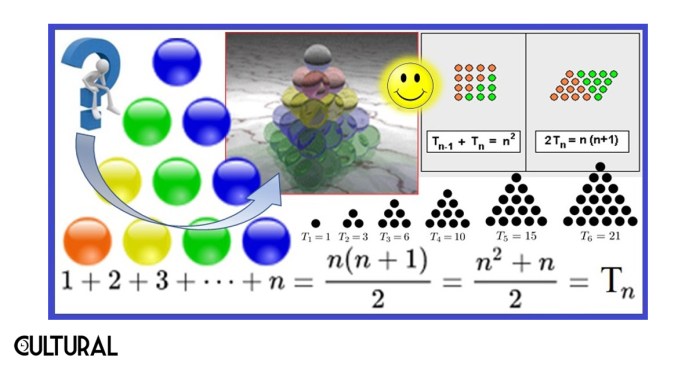
Existen una serie de curiosidades en torno de los números figurados.   Por ejemplo, en la imagen anterior aparecen los primeros números triangulares (1, 3, 6, 10, 15…), así como los primeros números cuadrados, que seguramente resultan más familiares para quien nos lee (1, 4, 9, 16…).  Es fácilmente comprobable que la suma de dos números triangulares consecutivos será cabalmente un número cuadrado.  Verifíquese esto en la lista anterior: (1, 3, 6, 10, 15…).   Varios juegos pueden ser planificados en torno de las figuras y el número de los objetos que las conforman.

Por este rumbo de ideas, quizá valga la pena una rápida digresión, siempre relacionada con estos números figurados.   Resulta que, en la Antigüedad, los conocimientos, mucho menores a los actuales, pero tampoco despreciables en riqueza y cantidad, no se hallaban tan dispersos, como se encuentran actualmente, totalmente desperdigados y en lo absoluto disconexos, por expresarlo de cierta forma.    Por ejemplo, estoy seguro que casi todos y todas quienes hemos pasado por la escuela secundaria sabemos dar lectura a la expresión «x²», interpretando, leyendo, «equis al cuadrado». Sin embargo, no nos detenemos ni reparamos en el posible significado y el origen de la palabra «cuadrado» en tal expresión.

Respecto a lo primero, el significado, sabemos que es una abreviatura para una operación aritmética con «números», una que se traduce en el resultado de multiplicar el valor que posee la variable «x» consigo misma, esto es, una expresión para el producto del valor de x multiplicado por ese mismo valor x. A algunos quizá les empiece a provocar dolores de cabeza pensar en todo esto, asociándolo a un embrollo, una complicación, de naturaleza más emocional que racional. Por ello nuestra insistencia en la lectura de cosas quizá más sencillas, pero en la total intención de comprender un poco más la historia de las ideas y su trascendente importancia.  Al jugar con las figuras, comprenderemos el sentido de la palabra «cuadrado».

Pues bien, retornando, ahora te estamos presentando otro tipo de números, los números corteses, o números de escalera, como algunos les llaman.   El calificativo de escalera se debe, responde, al hecho de que, en efecto, se trata de una variedad de números figurados, que como se indica, adquieren la forma de escalera, escalonados.   En el fondo, refiere a una generalización de la idea de sumar los números consecutivos, pero no necesariamente empezando por 1, como sucede en los números triangulares, por lo que pueden ser considerados como una generalización de estos.

Se dice que un número es cortés si puede colocarse como una suma de números consecutivos, dos o más. Ejemplificando, hemos visto que el 6 es triangular, pues 6 = 1 + 2 + 3; de hecho, T₃ = 6, pues se suman los números naturales hasta el tres, o bien, se verifica que T₃ = 6 = ½ (3) (3+1).   El número 6 es también un número cortés, pues es la suma de enteros consecutivos, a saber: 1, 2 y 3,

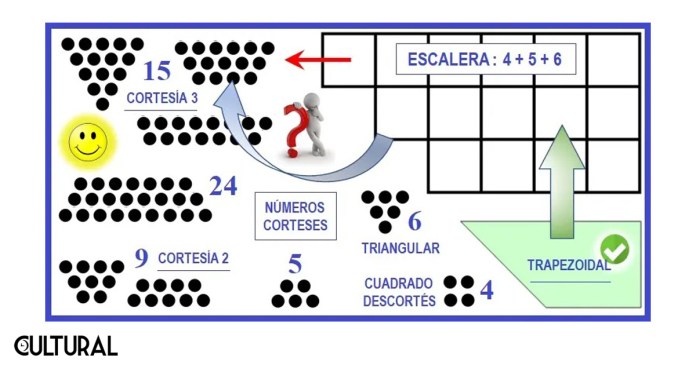
Dicho de otra manera, para que un número sea cortés, basta construir una «escalera» de sumandos consecutivos, por ejemplo, al tomar 2 + 3, o bien 5 + 6 + 7, que son «escaleras» de números enteros consecutivos.    La gracia está en verificar si un número puede colocarse en forma de escalera.   Si esto es posible, para alguna configuración, diremos que el número del total es cortés.  Así, por ejemplo, 5 = 2 + 3 es un número cortés, como también lo es el 18 = 5 + 6 + 7.   Nótese que por esta definición, todo número triangular, como 15 = 1 + 2 + 3 + 4 + 5 = T₅, también será cortés, siempre.

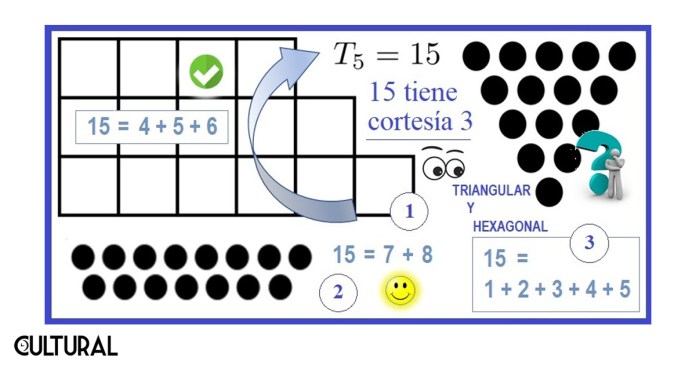
Por otro lado, resulta que un cierto número podría ser colocado como escalera de varias formas.   Es el caso del número 15, tenemos, para el cual tenemos, en particular, tres formas de colocarlo como suma de enteros consecutivos. En efecto, 15 puede colocarse como la suma anterior, pero también se tiene que: 15 = 7 + 8 = 4 + 5 + 6.   Así, vemos que hay tres formas de colocar a 15 como una escalera, como se aprecia en la imagen siguiente.

En contraposición, por otro lado, si se prueba con el número 16, se verá que no es posible encontrar una escalera que sume 16, de forma que 16 no es cortés, o bien, si se quiere, podríamos decir que el 16 es un número descortés.   Tenemos así que, con base al procedimiento descrito, podremos tener que un número es cortés o no lo es.   En todas estas temáticas de «tipos de números», está tácito que nos encontramos en el ámbito de los números naturales: ℕ = {0, 1, 2, 3, 4, …}.

Tómese en cuenta que, al definir un cierto tipo de número, léase par, perfecto, triangular, semiperfecto, primo, cuadrado, múltiplo de 5, cortés o de cualquier otra clase, automáticamente, en una lógica binaria, de dos valores de verdad, con un tercero excluido, estaremos definiendo los que no son, partiendo el conjunto ℕ en dos.

En general, toda posible clasificación, como la clasificación de Nicómaco, es una partición del conjunto del discurso (en este caso ℕ) en varias componentes, las partes del mismo. Así, un número natural será par o no lo será, será triangular o no, será cortés o no, etcétera. Entonces, dado que cuando un número que no es par decimos que es no par, o impar, de igual manera si un número no es cortés será no cortés, o descortés, como hemos apuntado, para el caso del 16.   La clasificación de Nicómaco parte el conjunto ℕ de los números naturales en tres tipos: defectuosos, perfectos o excesivos.   En la imagen siguiente el concepto y los listados con los primeros ejemplos.

Invitamos al lector y a la lectora que verifiquen que casi todos los números naturales son corteses. Si pruebas con el 19, por ejemplo, que es impar y también primo, verás que puede descomponerse como 9 + 10, una escalera de dos sumandos.  Al probar con 35, encontrarás que también es cortés, pero a diferencia del 19, 35 puede expresarse en varias sumas escalonadas, de enteros consecutivos. Búscalas y verás que son tres formas distintas (un pequeño reto para ti). Entonces surge la pregunta: ¿cuáles serán los números descorteses? ¿Serán finitos en cantidad o no tendrán límite? Ya hemos dicho que 16 no es cortés. ¿Pero podremos caracterizarlos, saber qué forma tienen?

Si pruebas con los números de una cifra, del 0 al 9, verás que no podrás descomponer en escalera los siguientes: {0, 1, 2, 4, 8}. Si a esto agregas el 16, que ya hemos mencionado, podrás realizar una pequeña conjetura, bastante fácil y razonable.   Observa los que han resultado descorteses: {0, 1, 2, 4, 8, 16}.   Todos los anteriores, que son números descorteses, son potencias de 2, exceptuando el 0.   Observa: 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16.  Lo inmediato que se nos ocurre es ir con el 32 = 2⁵.   Cabalmente veremos que no podremos colocarlo como una suma de números consecutivos.

Entonces tenemos una conjetura, razonable, que en este caso es verdadera.   No obstante, no vamos a demostrar acá tal aseveración, lo cual sería, para un matemático profesional, no excusable.   El teorema diría que, un número natural (positivo, o sea, distinto de 0) es descortés, si y solo si es una potencia de 2, esto es, tiene la forma 2ⁿ, para algún número natural n.  Lo anterior viene a decirnos que casi todo número natural es cortés, a menos que, como estamos diciendo, sea una potencia de 2.

Como gracia, si has nacido en un día que no sea el 1, el 2, el 4, el 8 o el 16 del mes, entonces has nacido en una fecha que corresponde a un número natural cortés. Si llamamos, y esto es una definición nueva en un nuevo sistema, cuyo dominio son los seres humanos, «ser humano descortés» a todo aquel o aquella nacidos en los días de la lista precedente, cabe preguntarse quiénes a tu alrededor serían personas descorteses.    De acuerdo con esta definición que estamos colocando, ¿Será el lector o lectora una persona cortés o descortés?

Por otro lado, sabiendo que son 5 x 12 = 60 los días del año que refieren a esa fecha (pues son cinco días por mes y son doce los meses del año), tendremos que la frecuencia o probabilidad de que alguien sea descortés sería de 60/365 = 16.4 %, aproximadamente, asumiendo que no hay días predilectos o más abundantes para nacer. Pero bien, si alguien ha nacido en estos días, tranquilos todos y todas, pues está claro que únicamente estamos jugando con los formalismos y posibles definiciones, o lo que es igual, haciendo matemática a nuestro gusto y antojo.

Estando claros que hay números que son corteses y otros que no lo son, cabe preguntarse a qué refiere el titular, que habla de la cortesía de un número.   Por ahora, únicamente sabemos que la cortesía de las potencias de 2 es nula, pues son totalmente descorteses.   En efecto, resulta que la cortesía no es nada más que el número de maneras distintas, sin tomar en cuenta el orden de los sumandos, que un número cortés puede ser escrito en forma de escalera.   Ya hemos mencionado que el número 15 puede ponerse como escalera de tres maneras diferentes, como se muestra en la siguiente imagen.   La cortesía del número 15 es 3.

Por otro lado, tenemos el número 14, para el cual, dado que únicamente puede ponerse como 2 + 3 + 4 + 5, se tendrá una cortesía de 1.   También hemos dicho que 35 tiene cortesía 3, pues puede escribirse como suma de tres escaleras distintas, que hemos dejado de tarea a quien nos lee.   Resulta divertido tomar un número cualquiera, de dos cifras, para no hacerlo muy difícil, y tratar de calcular la cortesía, es decir, tratar de ponerlo como escalera de todas las formas posibles.

Ante las posibles dudas de si hemos completado todas las opciones tipo escalera, la pregunta aquí será si podemos saber anticipadamente cuál es la cortesía de un número dado, sin tener que probar todas las posibles opciones.   Es decir, ¿podremos calcular de alguna forma la cortesía de un número natural dado?   Por ahora solo sabemos que, si el número es de la forma 2ⁿ, su cortesía será 0, o lo que es igual, se tratará de un número descortés.   Para lograr este objetivo, del cálculo de la cortesía de cada número natural, tendremos que apelar a la descomposición del número en cuestión en factores primos, que siempre existe y es única, según nos lo indica el teorema fundamental de la aritmética.

Los retos como el planteado resultan, por lo general, muy motivantes.   Mi experiencia en las columnas de difusión, Quadrivium, Episteme y Autómatos, me ha llevado al convencimiento de que es posible transformar en agradables las experiencias de aprendizaje con temáticas que permitan actividades lúdicas, superando el rechazo y los sinsabores que muchas veces la escuela nos traslada, por un mal abordaje y poco aprestamiento cognitivo y de todo tipo con relación a los tópicos curriculares de interés.   Por ello, quizá convenga, antes de continuar, regresar al ejercicio propuesto, en el que se solicitaba encontrar las tres descomposiciones en suma tipo escalera del número 35.

El concepto básico de la «cortesía» de un número se ilustra en los pocos ejemplos de las imágenes anteriores.   En particular, se observa el caso del número nueve, que tiene dos descomposiciones aditivas que cumplen con el formato de escalera, a saber: 9 = 4 + 5 = 2 + 3 + 4.   Lo que se ha dicho es que el número 35 tiene exactamente tres descomposiciones de este tipo, y se ha pedido hallarlas.   Sin mayor demora, la respuesta viene dada por: 35 = 17 + 18 = 5 + 6 + 7 + 8 + 9 = 2 + 3 + 4 + 5 + 6 + 7 + 8.

En estos dos casos, del 9 y del 35, decimos que la cortesía de cada uno es, respectivamente, 2 y 3, porque tienen, cabalmente, ese número de posibles descomposiciones en escalera, o descomposiciones trapezoidales, denominación que obedece a la forma que asumen las descomposiciones al representarlas mediante fichas u objetos uniformes, como se puede apreciar en una imagen previa.

Reflexionando al respecto, podemos descubrir que cualquier número impar es un número cortés, pues se puede descomponer (aditivamente, como una suma) usando una escalera de dos sumandos, siendo estos sus «casi mitades».   Véanse los ejemplos: 17 = 8 + 9, 31 = 15 + 16, 99 = 49 + 50, 601 = 300 + 301 y así en cualquier otro caso de un número impar.

Cabe observar que en las otras dos descomposiciones de 35 aparecen cinco y siete sumandos respectivamente. Lo curioso acá es que en el centro de la descomposición que tiene cinco sumandos está el 7, pues 35 = 5 x 7, interpretado como cinco veces 7, mientras que en la de siete sumandos, al centro veremos al 5, pues 35 = 7 x 5, que leeremos, y comprenderemos, como siete veces 5, dado que la suma 2 + 3 + 4 + 5 + 6 + 7 + 8 podría ser substituida por una suma de siete sumandos todos iguales a 5, esto es 7 x 5 = 35. Seguro estaremos regresando a esto en futura ocasión, pero por ahora lo dejamos aquí.

La reflexión sobre el quehacer matemático y la finalidad de esta ciencia formal puede ser extraída de los párrafos anteriores. Por ejemplo, estamos mencionando una conjetura: que todo número que no es par puede ser colocado como la suma de dos números consecutivos. Sin embargo, lo fundamental aquí, es que en Matemática no basta una verificación de casos, por muchos que podamos verificar. Se pedirá una prueba, una demostración para aceptar una verdad.

Si alguna persona verificara muchos, pero muchos casos de números impares, evidenciando que cada caso checado es un número cortés, esto no será aceptado como criterio de verdad, básicamente porque el total de instancias de números impares es infinito en cantidad, y una persona solo podría verificar un número finito de casos. En contraposición, al presentar una prueba formal, podremos aceptar el teorema que dice: todo número impar es un número cortés. La prueba de este teorema, que no es difícil, «se ve» así: 2n + 1 = n + (n + 1), partiendo de que un número que no es par siempre puede ser representado como 2n + 1, para algún número natural n.

Comprendemos así que la esencia de la Matemática es la demostración de hechos que no son evidentes, pero que, estando semánticamente contenidos en los axiomas, pueden ser derivados (deducidos) de estos, mediante la sintaxis de la lógica subyacente aceptada en el sistema del que se trate.

Hemos enunciamos arriba un teorema relativo a los números corteses, uno que no demostraremos, sino que, como es usual, nos conformaremos por comprender y poder aplicar. Hemos dicho que todos los números naturales positivos, que no son cero (ℕ* = {1, 2, 3, 4…} = {0, 1, 2, 3, 4…} – {0} = ℕ – {0}), son números corteses, con la única excepción de las potencias de 2, de la forma 2ⁿ. Así, si tenemos un número natural cualquiera que no sea potencia de 2, este podrá descomponerse en al menos una suma de tipo trapezoidal, de números consecutivos. El número de posibles descomposiciones en escalera (trapezoidales) será llamada la cortesía del número en cuestión.

En una de las imágenes previas se ilustró el hecho de que el 15 tiene cortesía 3, pues son exactamente tres las sumas en escalera que pueden encontrarse, a saber: 15 = 7 + 8 = 4 + 5 + 6 = 1 + 2 +3 + 4 +5.   También hemos citado al 9, con cortesía 2, y al 35 con cortesía 3.  Un impar como 17, o en general cualquier número primo p (que no sea par, esto es p > 2), tendrá únicamente una cortesía, o bien cortesía 1, con la descomposición elemental, en dos sumandos, que hemos ejemplificado en lo precedente, con sus dos casi mitades, como en 17 = 8 + 9.

La pregunta que pasamos a responder es: ¿podemos saber cuál es la cortesía de un número dado? Esto se entiende como si podemos saber anticipadamente, sin probar sacar (a fuerza bruta) todas las posibles descomposiciones aditivas trapezoidales del número de interés. La respuesta es sí, y sin prueba, ni mayores razonamientos (que es como el sistema educativo nos ha «malcriado»), procederemos a describir el procedimiento (o algoritmo, para usar la palabra de moda, que existe desde los tiempos de la Arabia medieval). Lo hacemos así por el espacio y en función de aterrizar en una utilidad tangible que a más de alguno y alguna podrá servir.

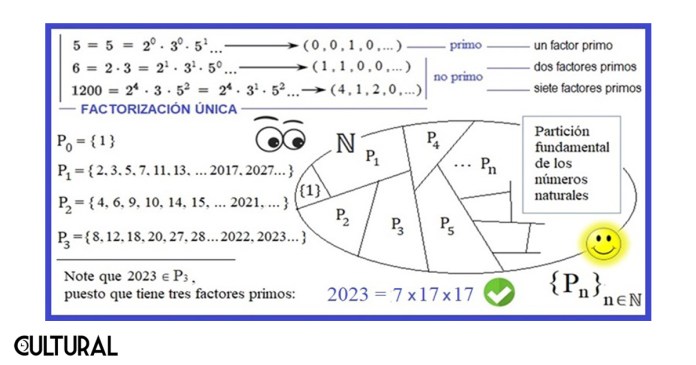
Para ver el procedimiento, es necesario recordar la partición de los números naturales positivos ℕ* = {1, 2, 3, 4…} = {0, 1, 2, 3, 4…}, de acuerdo y según sea el número de factores primos que contiene su descomposición.    Como hemos dicho, cada número natural tiene una descomposición en factores primos que es única.   En la imagen que sigue se muestra las partes P_n de la partición, donde P_n simboliza todos los números naturales que son el resultado del producto de n números primos en P₁. el conjunto de los números primos.

El primer paso es descomponer el número de interés en su factorización primal única, esto es, colocarlo como producto de los factores primos que lo generan.  El teorema fundamental de la aritmética nos garantiza que esta descomposición existe y es única.  Por ejemplo, citamos que la factorización de mil doscientos es: 1200 = 2⁴ x 3¹ x 5².

Como un paréntesis, también de utilidad, resulta que el número de divisores de 1200 puede ser obtenido de los exponentes de los factores anotados. Para ello, tómense los exponentes, que en este caso son 4, 1 y 2, y súmesele una unidad a cada uno, para obtener: 5, 2 y 3. Entonces, el número de factores posibles, es decir, de divisores de 1200 será igual al producto de esta secuencia: 5 x 2 x 3 = 30 divisores de 1200. Haga nuevamente el esfuerzo quien nos lee, y verá que, en efecto, 1200 tiene 30 divisores, empezando por 1 y terminando en él mismo, 1200.

El algoritmo para obtener la cortesía es bastante similar al descrito, con la excepción de que se tomarán únicamente los exponentes de los primos impares, esto es, de todos los factores primos, excepto del 2.   En el caso de 1200 = = 2⁴ x 3¹ x 5², hemos apuntado que los exponentes son 4, 1 y 2, de los factores primos 2, 3 y 5, respectivamente.

Pues bien, olvidando la potencia de 2, como que si no existiera, tendremos los exponentes 1 y 2, correspondientes a los factores primos 3 y 5.   Entonces agregamos una unidad, obteniendo 2 y 3, de donde: 2 x 3 = 6 son las formas posibles. Sin embargo, al final restaremos uno, teniendo 5 como resultado, lo que se traduce en que la cortesía de nuestro ejemplo es 5, las cinco formas de descomponer 1200 como suma trapezoidal.   En el caso del 35 = 5¹ x 7¹, tomamos los exponentes, 1 y 1, de donde sumando 1 se tiene 2 y 2, por lo que la cortesía de 35 será, como hemos visto al inicio, 3 = 2 x 2 – 1.

Para ilustrar, en la imagen siguiente se puede apreciar otro ejemplo, el caso del número 90, que se factoriza así: 90 = 2¹ x 3² x 5¹.  Como vemos, 90 posee dos factores primos impares, o sea, los primos que son distintos de 2, siendo sus exponentes 2 y 1, respectivamente. Así, por el teorema de la cortesía (nombre que me estoy inventando en este momento, cosa perfectamente válida al «hacer matemática»), la cortesía de 90 será de una unidad menos que 6 = 3 x 2 = (2 + 1) (1 +1), esto es, 90 tiene cortesía 5.

De todo ello, surge un nuevo reto para el inquieto lector o la lectora que gusta de la exploración y el cuestionamiento: encontrar las cinco descomposiciones trapezoidales (o en escalera) que posee 90. Al hacerlo podrá entrever lo natural que es para el ser humano la búsqueda de la sistematización y la generalización de los procedimientos, puesto que todos llevamos adentro un pequeño matemático, poeta, músico y loco, como dice el viejo adagio. No podemos, por otro lado, negar el profundo placer que de todas estas actividades puede surgir.

Queremos, finalmente, insistir en la necesidad y la importancia de la prueba como eje basal de todo el edificio matemático deductivo. Para que de la conjetura se pase al teorema será necesario un camino de formalismo y genuino esfuerzo intelectual. Empero, para que la conjetura brote, será necesario el aprestamiento y la exploración lúdica. En ello, fundamental es reparar que la infinitud de los casos, cosa inexistente en nuestro mundo tangible, de los sentidos y de la realidad física, hace necesario un camino diferente al de la verificación de individuo a individuo. Es requerida la demostrabilidad y la deducción, partiendo de un basamento teórico suficiente.

En breve, como un ejemplo complementario, dados los infinitos triángulos rectángulos, aunque verifiquemos que el teorema de gou gu xian se cumple en algunos de ellos, será necesaria esa prueba que los antiguos, no solo los chinos, sino en todas las grandes civilizaciones, procedieron a realizar. El sentido de la prueba y del dominio de mundos coherentes, consistentes, viene de esta indefectible necesidad, pues la inconsistencia es en lo absoluto aceptable para la existencia razonable y con sentido. Nos despedimos, con cortesía, con este último párrafo que, se podrá verificar, contiene un número cortés de letras, y también de palabras.

Finalizo citando a René Descartes, quien, hablando de Geometría, escribió: «Espero que nuestros nietos me estarán agradecidos, no solamente por las cosas que he explicado aquí, sino también por las que he omitido, intencionadamente, a fin de dejarles el placer de descubrirlas».

Fuente de imágenes    :

[ 1 ] Imagen editada por Vinicio Barrientos Carles   

[ 2 ] Imagen editada por Vinicio Barrientos Carles    ::    IMO, YouTube y Wikipedia, además de fotos personales de Abigail Enríquez y Ana Rojas.

[ 3 + 4 ] Imágenes elaboradas por Vinicio Barrientos Carles con base en figuras tomadas de Wikipedia

[ 5 … 9 ] Imágenes elaboradas por Vinicio Barrientos Carles.