Grandes, pero finitos

Vinicio Barrientos Carles

Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior.   Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar.   Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.

Quien busque el infinito, que cierre los ojos.

Milan Kundera

De niño tuve más de una maestra que, en su momento, se vio en la obligación de explicarnos que existían dos tipos de conjuntos, a saber, los que eran finitos, porque se podían contar sus elementos, y los infinitos, que, en contraposición, aunque se quisiera contar sus elementos, nunca se podría determinar con un número natural su correspondiente cardinalidad.   Para ilustrar esta idea de finitud, un tanto abstracta, nuestras profesoras recurrían al uso de ejemplos.   Presentar casos de conjuntos finitos era muy sencillo.   Empero, no resultaba así al intentar ejemplos de conjuntos infinitos.

En el esfuerzo por ilustrar la infinitud, se solía recurrir al conjunto conformado por todos los granos de arena de mar, es decir, por el conjunto de la totalidad de granitos de arena en todo el planeta.   También se solía citar aquella colección constituida por todas las estrellas del cielo, o también por aquel integrado por todos los cabellos en la cabeza de alguno de nuestros congéneres.   Cuando se citaban las estrellas del firmamento, se decía: «el conjunto de planetas del Sistema Solar es finito, pues se puede enlistar, pero no así la colección de todas las estrellas del firmamento».   Se seguía, al afirmar esto, el modelo cosmológico de un cosmos infinito, como el descrito por los contemporáneos a sir Isaac Newton.

Sin embargo, aún para un niño, no quedaba tan claro que no se podría terminar de contar los elementos de estos ejemplos de supuestos conjuntos infinitos.   Algunos estudiantes objetaban, pero sus comentarios nunca serían tomados en cuenta.  Después de todo, quitando pelo por pelo, sin importar la cabeza de la que se tratara, se tenía que llegar a un final, en donde ya no quedará más pelo que agregar a la lista.   El conjunto así, en efecto, resultaba finito, pues algún número natural correspondería a la totalidad de cabellos.

De similar forma en el caso de las arenas del mar, pues es posible percatarse de que si continuamos, grano tras grano, tras grano, tras grano, colocándolos imaginariamente en un gigantesco y adecuado recipiente, inexistente en la realidad concreta, pero existente a nivel mental, arribamos a la conclusión de que sí llegaremos al final de la cuenta, pudiendo colocar el último de los granos de arena de todos los mares del planeta, y por lo tanto el proceso de conteo terminará en un cierto número, verificando que se trata de un conjunto finito, muy grande, pero no infinito como alguien podría proponer, incluyendo a aquella maestra que nos lo colocaba como ejemplo de conjunto infinito.

 

Destaca y cabe mencionar que esta conjetura sobre la infinitud de las arenas del mar es, efectivamente, histórica, pues se tiene conocimiento que Arquímedes de Siracusa, el gran matemático griego de la Antigüedad, realizó una tarea interesante, inspirado en un verso del poeta Píndaro que expresa «infinitas como las arenas del mar».   De hecho, el genial siracusano desarrolló en su texto Arenario, dos loables tareas: calcular el número de granos de arena que pudieran llenar completamente el universo según el modelo de Aristarco de Samos, y crear un sistema de numeración verbal y conveniente en el cual resultara posible nombrar tal número.

Y es que la infinitud es uno de los primeros procesos matemáticos abstractos que la humanidad enfrentó, cuando se vio en la necesidad de sistematizar el conteo y construir un sistema de numeración convenientemente diseñado para identificar y nombrar números muy grandes, como el caso de los censos.  Es claro que, dada una determinada lista o conjunto, siempre será posible imaginar una lista aún mayor, de forma que, con relación al conteo de sus elementos, siempre existirá un número natural más grande que el anterior.   No obstante, es fundamental distinguir entre una cantidad muy grande, expresada con un número natural muy grande, y una cantidad ilimitada, infinita, para la cual no existe ningún cardinal finito.

En términos más formales decimos que dado un número natural n, resultado de un conteo, siempre será posible obtener uno mayor, que es el siguiente o sucesor, dado por la operación n + 1. La aritmética elemental está construida sobre un proceso computacional muy importante: la recursividad, de naturaleza intrínsecamente infinita y de la cual valdrá el esfuerzo de escribir en próxima ocasión.   Nótese que se asume que n + 1 > n, de donde vendría a ser imposible que n + 1 = n.   Empero, con los números transfinitos, esto no es cierto, pues una cantidad infinita incrementada en 1, o en cualquier número finito, no se incrementará, sino permanecerá igual.

Lo anotado en el párrafo anterior puede formalizarse así: si n es de tamaño infinito, n + 1 = n + m = n, para cualquier número m finito.   También se podrá tener que una parte propia es de «igual tamaño» que el todo, si este todo es infinito.   Así, observamos que tampoco se cumple un presupuesto coloquial básico que reza que el todo es mayor que las partes.   Si se repara en el adagio, se verá que no se cumple para objetos infinitos.   Estas y otras aparentes paradojas asombraron al mismo Georg Cantor, el matemático alemán que a fines del siglo XIX formalizó las ideas de cardinales infinitos, que son de varios tipos y tamaños, así como la teoría de ordinales transfinitos.

 

 

Como expresa Milan Kundera en la frase citada al inicio, los procesos recursivos, o de recurrencia, son de naturaleza intrínsecamente abstracta, pues se trata de un seguir, y seguir, y seguir, indefinidamente y sin paro posible, como bien describe Edgar Allan Poe en su cuento El pozo y el péndulo: «Transportándome silenciosamente hacia abajo, aún más hacia abajo, cada vez más abajo, hasta que me invadió un vértigo espantoso a la simple idea del infinito en descenso».   Al reflexionar, caeremos en la cuenta de que nuestras maestras buscaban ejemplos concretos, tangibles, de conjuntos infinitos.  Tal tarea resulta imposible, pues el infinito es una idea que solo puede existir en el mundo ideal.

Dicho en otras palabras, en el mundo sensible, en la realidad concreta, no existen conjuntos infinitos.   Por ello, insistimos, resulta relevante y fundamental la distinción entre un número muy grande y el infinito, que es un producto mental (de naturaleza lógica ideal), que hoy en día estamos claros que no se corresponde con nada de nuestra realidad sensible. En este sentido, desde los inicios de la Modernidad hemos ido aprendiendo que nuestro universo físico es finito, y por grande que pueda resultarnos, tiene fronteras y un final.

En el artículo «Nuestro universo visto desde el Webb», a propósito del lanzamiento de este observatorio espacial, acaecido hace ya casi un año, comentábamos sore la finitud del cosmos, pero, también, sobre nuestra pobre percepción sobre su tamaño, no teniendo claro, por ejemplo, hasta donde se extiende nuestro sistema estelar, en los confines remotos de la nube de Oort.   Todo sirva para distinguir, de tajo, entre un infinito, ideal, y una cantidad o magnitud muy grande, para nosotros, pero, en primera y última instancia, finita.

De similar manera a nuestra limitada y pobre captación de las magnitudes físicas muy grandes, pero finitas, igual sucede con los números naturales grandes, que podríamos a considerarlos infinitos, por ser tan grandes.  Hoy estamos presentando cuatro categorías para la magnitud de un número finito.   Los infinitos los dejaremos para una próxima oportunidad.   Por ahora estar claros que un número natural determinado es finito pues siempre lo podemos corresponder con el conteo de los elementos de un conjunto no infinito.

Igualmente, si tratamos con un número racional o un número real, entiéndase, los que poseen cifras decimales, siendo resultado de una medición, podremos establecer que se trata de un número racional o real acotado, si es no infinito, al encontrar un número natural mayor que el número dado.   Así: r ∊ ℝ es finito si existe un N ∊ ℕ tal que r < N.   Esto significa que r está acotado por N.

El astrofísico, exobiólogo y divulgador de la ciencia Carl Sagan grabó un fabuloso vídeo en el cual enfatiza la diferencia entre el infinito y cualquier número natural, por grande que sea.    Invitamos al lector y lectora que nos siguen a ver el vídeo (es corto, menos de 4 min), en el cual presenta un notable y a la vez famoso número grande, el googol (gúgol), y otro pariente de este que es aún mayor, el googolplex (gúgolplex).

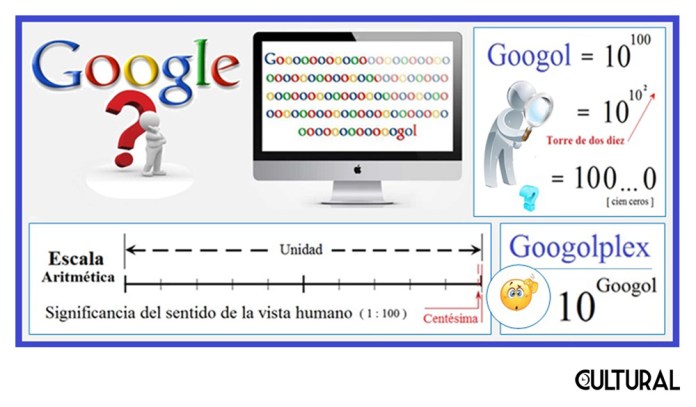
¿Qué es exactamente un googol? Pues es uno de los números grandes con nombre propio que sirve para ilustrar el horizonte limítrofe que separa a los números normales de esos que se empiezan a considerar números grandes. Un googol es, básicamente, en el sistema de numeración decimal, un dígito uno seguido de cien ceros, lo que es equivalente a afirmar que es el resultado de elevar diez a la centésima potencia.   En la imagen siguiente ilustramos este concepto del googol, incluyendo una escala aritmética, en la que se muestra una centésima de la unidad mostrada.  Nótese que la vista y, en general, nuestros sentidos físicos, son un primer parámetro de la magnitud de un número.

 

De lo anterior, tenemos una primera categoría, los números perceptibles, como aquellos de cero a cien, o de un orden de magnitud por el estilo.   El otro límite o frontera vendrá dado por este numerito tan singular, el googol.   Podremos llamar a los números comprendidos entre 100 (10²) y el googol (10¹⁰⁰) como números estándar, nuestra segunda categoría, considerando como números grandes, en la tercera categoría, aquellos números que viene a ser significativamente mayores que un googol.   Sin embargo, aunque quien nos lee no lo crea, veremos que existe una cuarta categoría: los números muy grandes.

Por otro lado, como se menciona en el vídeo de Sagan, a manera de curiosidades, el término googol fue acuñado hace casi un siglo, en 1938, por Milton Sirotta, un niño de nueve años, sobrino del matemático estadounidense Edward Kasner, quien compartió el concepto en su libro Las matemáticas y la imaginación.   A este respecto, Isaac Asimov dijo en una ocasión: «Tendremos que padecer eternamente un número inventado por un bebé». También, de forma interesante, es cierto que la empresa Google cambió en 1997 su nombre al actual, inspirada en el número googol, señalando que se escribe diferente, paradójicamente, por un error ortotipográfico de quien lo transcribió.

A pesar de la connotación del googol como una frontera entre los números estándar y los llamados números grandes, establecer más formalmente cuándo un número deja de ser pequeño tiene que ver con la forma en que procesamos la información cuantitativa.   Para ilustrar, hace ya décadas que nuestras calculadoras portátiles tienen la capacidad de escribir cantidades virtualmente equivalentes a un googol.   En el caso de nuestra mente, tiene que ver con la significancia de una cantidad y qué tanto podemos discriminar, mentalmente, el tamaño del número natural dado (obsérvese que no necesitamos contar para saber que una colección de objetos tiene tres o cuatro, y que sí al tratarse de siete, pues no podemos percibirlos de golpe).

De esta guisa, en función de las limitaciones de nuestros sentidos y de nuestras capacidades mentales, el uso que damos al sistema de numeración decimal se ve reducido, en la práctica, al empleo de unos pocos dígitos.  Por ejemplo, regresando al particular caso del sentido de la vista, que nos ayuda a cuantificar nuestro entorno, caemos en la cuenta de que nuestros ojos pueden distinguir al nivel de una décima parte, o de una centésima, a lo sumo, pero no más, por lo que la significancia se verá reducida a dos cifras decimales, que son las que solemos utilizar al expresar las medidas racionales de las cantidades que nos interesa cuantificar, entiéndase el dinero y otras magnitudes de tipo físico.

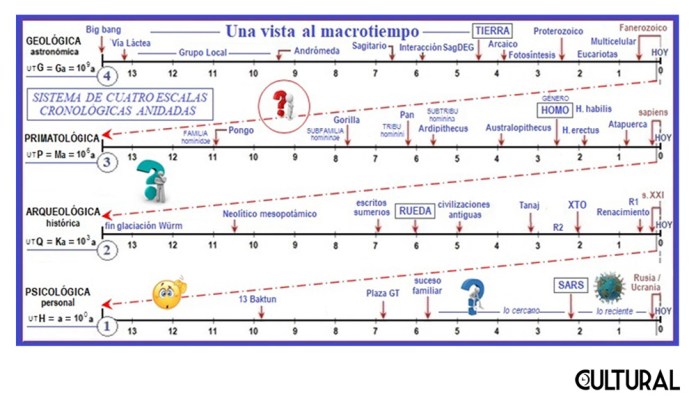
Cuando deseamos representar números de más de dos cifras, es usual recurrir al uso de escalas geométricas, o más frecuentemente de varias escalas aritméticas sucesivas, cada una con unidades más grandes o pequeñas en una cierta razón que resulta conveniente. Por ejemplo, si deseamos visualizar el aparecimiento del ser humano (circa 1 Ma, un millón de años) en comparación con la edad de nuestro universo físico, será necesario recurrir a varias escalas con cierta graduación entre sí.   Esta técnica de escalas aritméticas anidadas la hemos usado en nuestros artículos más recientes, al hablar de la evolución y la complejidad.   En la imagen que sigue una representación del tiempo del cosmos mediante cuatro escalas con una ampliación de factor mil.

Nótese que la edad estimada del universo es de 13.8 millardos de años, es decir de una cantidad aproximada de un 1 seguido de diez ceros de años, lo cual es realmente una cantidad increíblemente pequeña comparada con un googol de años.   De hecho, en nuestro horizonte cosmológico o universo observable todas las cantidades físicas, sin importar las unidades que se utilicen para determinarlas, vendrán expresadas con números que resultarán siendo tremendamente mucho más pequeños comparadas con el número que en esta ocasión hemos presentado, y vale aclarar que este número, el googol, que es 10¹⁰⁰ será extremadamente pequeño comparado con otros, que estaremos presentando al final de este artículo.   A estos números les llamaremos «muy grandes».

 

Sumarizando lo previo, diremos que apuntamos el discurso hacia los números grandes, planteando, desde un inicio, la distinción fundamental que existe entre una cantidad exageradamente grande, quizá muy difícil de imaginar, y una cantidad infinita.   Hemos apuntado que el infinito es una creación abstracta de tipo matemático, basada en la recursividad, la cual da origen a procesos que se pueden autollamar indefinidamente, generando la noción del infinito como una pura entelequia para el sinfín de algo.

Esta separación entre la finitud y el infinito fue recalcada en el vídeo de Carl Sagan, el gran divulgador de la ciencia, quien a la vez nos ha posibilitado presentar uno de los más famosos números grandes, el googol (gúgol), y otro que se deriva del mismo, el googolplex (gúgolplex).   En la construcción del googol y el googolplex, es posible descubrir la esencia del mecanismo para la construcción de los números grandes, a saber, la iteración, repetición, de una misma operación o proceso generativo.

Así, los números naturales se construyen y se calculan mediante un proceso repetitivo, sumar uno al anterior. Podría sumarse otra cantidad y tendríamos el concepto de una escala aritmética, en donde se grafica una sucesión o progresión aritmética.   El proceso repetitivo puede ser otro, por ejemplo, el de la multiplicación, en cuyo caso tendríamos una escala geométrica, correspondiente con una progresión geométrica, la cual, a su vez, está basada en la multiplicación iterada, que genera la exponenciación.  La utilidad de las escalas geométricas es grande, porque casi cualquier número o cantidad obtenida por conteo o por medición de alguna magnitud en el mundo sensible puede ser explicado y se encuentra contenida en una escala geométrica seleccionada convenientemente.

 

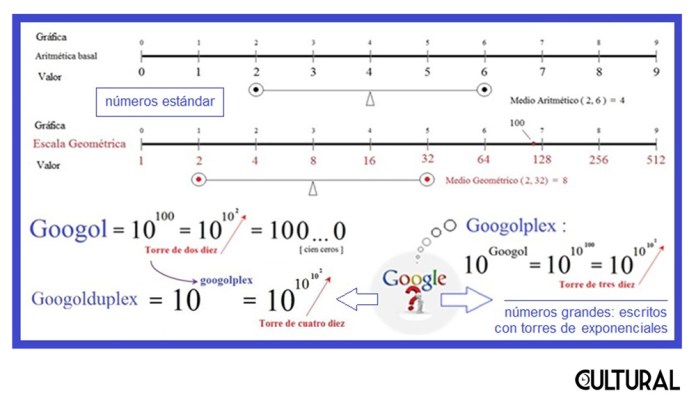
Podrá observarse que detrás de esta iteración subyace el concepto de recursividad, es decir, el llamado a un proceso fijo que se repite sobre el resultado previo obtenido de ese proceso. En la definición del googol esto es claro, pues se repite el número cero cierto número de veces (cien, para ser específico), después del uno inicial (en nuestro sistema decimal de numeración, claro), siendo por lo tanto el resultado de diez elevado a la centésima potencia.   Por otro lado, los que hemos llamado números estándar, entre 10² y 10¹⁰⁰, pueden ser representados en una conveniente escala geométrica, de similar forma a como los números perceptibles pueden ser representados y visualizados en una escala aritmética.

Lo admirable aparece al definir el googolplex, pues para escribirlo en sistema decimal se necesitará anotar un uno seguido de un total de un googol de ceros. El proceso puede continuar, pues un googolduplex se define como un uno seguido de un googolplex de ceros, así como un googoltriplex tendrá un número de ceros igual a un googolduplex, y así sucesivamente hasta donde el lector desee continuar.   Nótese que estamos hablando de torres de exponenciales con dos, tres y así sucesivamente, cantidades de bases diez, en el caso decimal.   Cualquier base natural mayor que 1 funciona similarmente bien.

Usar potencias de diez para números grandes es frecuente, y si se tratara de números mucho mayores, siempre podremos recurrir a las torres de exponenciales, ejemplificadas muy bien con nuestros amigos el googol y sus descendientes: googolplex, googolduplex, googoltriplex, etcétera. Nótese que esta notación-expresión de torres de exponenciales, mucho más potente que los conocidos exponenciales, en su versión particular de las potencias de diez, empleadas en la denominada notación científica, permitirán definir una nueva categoría, la tercera: los números grandes.

Así, se podrá observar que un googol puede ser representado como una torre de dos dieces, mientras que el inimaginable googolplex será expresado como una torre de tres dieces. Vale anotar que para escribir un googolplex, al ritmo de varios dígitos por segundo (no importa realmente cuántos dígitos por segundo puedas escribir), se necesitaría una cantidad de años superior a 10 elevado a la 92, cuando la edad de nuestro joven universo es de apenas, expresado en años, del orden de 10 elevado a la 10: 10¹⁰.    Nótese la inmensa diferencia de un número de diez cifras con otro que tiene noventa y dos cifras.   No se podría escribir el googolplex ni en toda la edad del universo.   Por ello no se trata de números estándar, sino de números grandes.

Un googol es un número suficientemente grande para representar la mayoría de los números que podrían interesarnos, estando todos estos números dentro del alcance proporcionado en una calculadora científica de bolsillo. Por ejemplo, el número total de partículas elementales en el universo es de alrededor de 10 elevado a la 80 (el número de Eddington).    Hemos mencionado en lo previo que Arquímedes calculó, en su texto El arenario, el número de granitos de arena con el que se rellenaría el universo en el modelo de Aristarco de Samos, de apenas 2 años luz de diámetro, aproximadamente, este sería inferior a 10 elevado a la 63: 10⁶³.

 

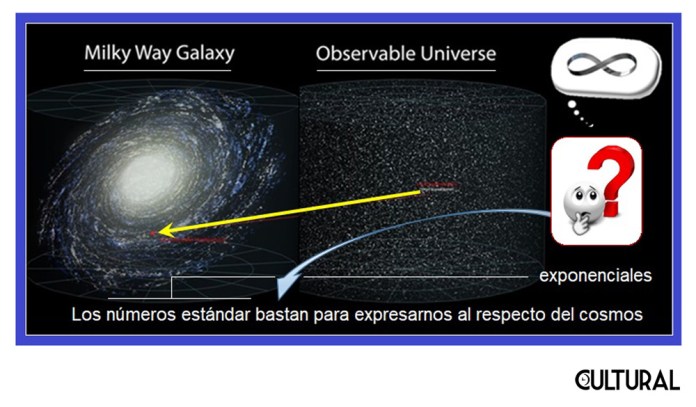
De manera similar, Sagan calculó que si todo el universo conocido, el universo físico nuestro, estuviera repleto de neutrones, uno pegado al otro (cosa imposible, por cierto), obtendríamos un número total inferior a 10 elevado a la 128, 10¹²⁸, lo que nos dice que con un googol podremos contar cuanta cosa física exista, y que realmente un googolplex es un número imposible de representar en el mundo material, y por consiguiente peor aún con sus descendientes dúplex, triplex, etcétera.

Para mencionar otra cantidad grande en nuestro universo físico, pero similar a un googol, anótese que el tiempo de decaimiento de un agujero negro súper masivo de aproximadamente la masa de una galaxia (equivalente a 10 elevado a la 11 masas solares: 10¹¹), debido a la radiación de Hawking, es del orden de 10 elevado a la 100 años, de donde se deduce que la muerte por calor de un universo en expansión tiene un límite inferior a un googol de años, tomando nota que la edad actual estimada del universo es de 13.8 millardos de años, es decir, en años, de apenas 10 elevado a la 10: 10¹⁰.

No obstante de lo fascinante del googol, en lo que sigue, que esperamos que no se extienda indefinidamente, hacemos una lacónica introducción a los denominados números muy grandes, en donde cabe citar el inimaginable número de Graham, construido con hiperoperaciones aritméticas, y el inentendible número de Rayo, construido por el filósofo y experto en metalógica, el mexicano estadounidense Agustín Rayo, como resultado de un duelo de números grandes realizado en el MIT el 26 de enero de 2007.

Aunque nos estamos extendiendo un poco, conviene recordar que, por mucho que se prolongara el escrito, asumiendo que nunca se parara de anotar, agregando letras y palabras sin tregua y sin descanso, siempre que el universo físico conocido siguiera existiendo, la longitud de ese hipotético escrito, medida por el número de letras utilizadas, sería siempre expresada por un número finito y limitado, bastante grande probablemente, pero nunca comparable con un número infinito, sin importar el ritmo con el cual las diferentes letras fueran colocadas en una inmensa tira de papel. Y es que podrán existir números grandes, y otros muy, muy grandes, pero siempre, en cualquiera de los casos, imposibles de equiparar con el infinito.

De lo anterior el lector podría cuestionar, preguntándose ¿pero entonces qué podría ser infinito? En breve podemos decir que el infinito es simplemente una entidad formal, la idea de algo que no tiene fin. De hecho, se trata de un producto mental de tipo matemático, y sin entrar en honduras y profundidades sobre lo que podría significar exactamente acá el calificativo de matemático, lo fundamental será establecer la distinción abismal entre lo que es finito y lo que no lo es.

Aun suprimiendo las entelequias filosóficas y el abordaje metafísico de lo infinito, cabe anotar que en la Matemática existen varias versiones de posible respuesta a la pregunta sobre qué es el infinito, distinguiéndose inclusive entre infinitos de diferente tamaño, es decir, unos infinitos pequeños y otros que resultan infinitamente mayores que los infinitos pequeños, y en esto no estamos recurriendo a ningún juego de palabras.

Por ello, en lo precedente, hemos insistido, cayendo en la necedad, al respecto de la finitud del universo físico.  Hemos anotado un hecho crucial: que nada sensible o concreto podría ser infinito. Sucede que cuando una cantidad resulta muy grande o colosal, se pierde en nuestra limitada imaginación, cayendo en la maliciosa tentación de pensar que se trata de una cantidad infinita, como en el caso de las arenas del mar, citado al inicio, o en las estrellas del universo, mencionadas después. En el primer caso, señalamos que el número de granitos de arena con el que se rellenaría el universo en el modelo de Aristarco de Samos, de apenas 2 años luz de diámetro, aproximadamente, sería inferior a 10⁶³, como bien lo calculó Arquímedes, varios siglos antes de nuestra era.

Por otro lado, con la cantidad de estrellas en el firmamento, tenemos que en una noche muy clara y muy despejada se podrán observar, a lo sumo, un número inferior a tres mil, es decir, del orden de magnitud de 10³.   En nuestra tipología numérica, o clasificación del tamaño de los números, hemos identificado como números perceptibles a aquellos números naturales de una o dos cifras, en el sentido de que son aquellas cantidades a las que tenemos acceso discriminante con el uso exclusivo de nuestros sentidos físicos.

A su vez, en una segunda categoría, hemos denominado números estándar a aquellos que provienen de conteos y de mediciones en nuestro mundo usual, y que por lo tanto no son, ni tan grandes ni tan pequeños (en el sentido de una escala geométrica), por lo que es frecuente utilizar el denominado orden de magnitud, que es el exponente de la cantidad escrita en la llamada notación científica, es decir, con un exponencial de base diez, o de otra base de numeración, si se utiliza un sistema de numeración diferente al decimal.

Cuán grande puede ser un número estándar, ¿cuántas serán las estrellas de todo el universo físico (observable)?  Bueno, se trata de 3 x 10¹¹ galaxias con un promedio de 4 x 10¹¹ estrellas cada una, por lo que resulta un número total de estrellas en todo el universo de (apenas) 10²³ aproximadamente. Si nos vamos al número de protones tendremos a lo sumo 10⁸³ partículas, y ya hemos comentado que el astrofísico Carl Sagan calculó que, si todo el universo conocido estuviera repleto de neutrones, uno pegado al otro, cosa también imposible, obtendríamos un número total inferior a 10¹²⁸.

Es decir que, en conclusión, nuestro viejo amigo el googol (equivalente a 10¹⁰⁰) es un número suficientemente grande para expresar cualquier cantidad física concreta, o cualquier posible resultado de una medición sobre objetos en el mundo sensible, y por ello el googol es considerado un buen punto limítrofe para el inicio de los números grandes, esos que ya no representan cantidades estándar del mundo real.

Obsérvese, por otro lado, que para cualquier número grande existirá otro similarmente pequeño, que le corresponde bajo la función inverso, o 1/x. Por ejemplo, al número 100 = 10² le corresponde 1/100 = 10^-2 = 0.01; para 100 000 = 10⁵ tendremos su contrapartida 1/100 000 = 10^-5 = 0.00001; para un googol = 10¹⁰⁰, que es un 1 seguido de cien ceros, o sea un número ya grande, tendremos el correspondiente inverso multiplicativo, igual a 1/googol = 10^-100 , que se escribiría en sistema decimal de numeración como 0.000…001, en donde se han escrito exactamente cien ceros en este último numeral.

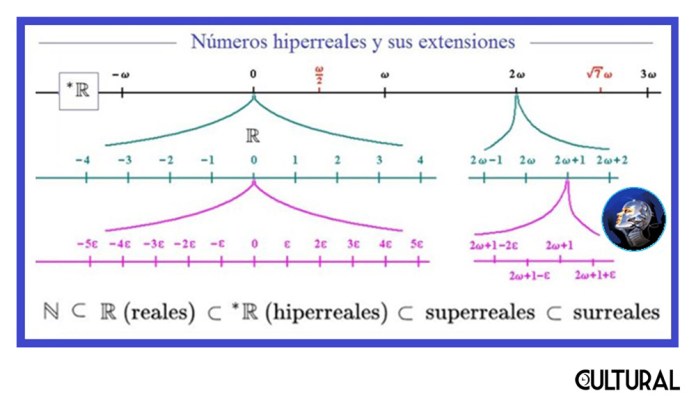
Obsérvese, en complemento, que para los números infinitamente pequeños sí existe un límite de lo infinitamente pequeño, que es 0, por lo que suele pensarse que el inverso del infinito (grande) es cero y viceversa. Consecuencia de esta propiedad es el hecho de que pensar en cantidades muy grandes, o inclusive infinitos, se corresponderá a concebir cantidades muy pequeñas, o infinitesimales, respectivamente. Este abordaje se tiene al desarrollar varias teorías de ampliación de los más conocidos números reales, como lo son los números hiperreales, superreales y sureales, todos provenientes y derivados del análisis no estándar, (desarrollado por Abraham Robinson en la década de los años setenta), teoría que permitió justificar rigurosamente el uso de números infinitos y de infinitesimales en el desarrollo temprano del Cálculo Infinitesimal del siglo XVII.

Aunque el uso de los exponenciales de base diez, las famosas potencias de diez, es frecuente y suficiente para los que acá hemos denominado números de tamaño estándar, resulta una notación insuficiente para los números grandes, más allá del googol. En efecto, traducir una torre de exponenciales tan sencilla como el googolplex resulta imposible en la notación exponencial. Este hecho nos proporciona un criterio. Si un número no puede ser representado fácilmente por medio de una potencia de diez, pero sí por una torre de exponenciales, podremos considerarlo un número grande, como el caso del googolplex o el googolduplex, así como todos sus parientes y vecinos.

En este momento podríamos pensar que las torres de exponenciales bastarían para anotar los números más grandes que alguna persona pudiera llegar a concebir, sin embargo, quizá no hemos reflexionado al respecto del meollo del crecimiento, el cual se basa en procesos iterativos y de recurrencia, unos que se llaman a otros previamente calculados. Por ejemplo, las sucesiones aritméticas y geométricas utilizan la adición y la multiplicación respectivamente; por otro lado, las torres de exponenciales provienen de la iteración de la exponenciación. En general, tenemos el concepto de hiperoperación que podremos presentar posteriormente.

Así, de esta forma, los números que ya no pueden ser representados por medio de extensas cadenas o torres de exponenciales son a los que hemos identificado como números muy grandes, los cuales no son muy sencillos de identificar.   Resulta difícil explicar su magnitud.   Uno de los ejemplos más utilizados para el caso de los números muy grandes es el denominado número de Graham, vinculado de alguna forma con la función de Ackermann, muy citada en la teoría de la computabilidad de las funciones recursivas.

En la imagen que sigue un esquema de cómo se construye, a partir de su definición, este pequeño monstruo.   El lector, lectore, no se preocupe si se queda todo esto un tanto nebuloso.   Sería verdaderamente bastante extraño que no nos sintiéramos así… un poco perdidos.   En el párrafo previo se ha incluido el enlace digital a Wikipedia, en la expectativa de si alguno o alguna quisiera ampliar.

 

La comprensión de un número como este y otros similares requerirá, en definitiva, un poco más de tiempo y de esfuerzo del que acá hemos invertido.   Empero, la motivación ha sido el de presentar un esbozo de la existencia de unas cantidades que escapan a nuestra imaginación y que, de hecho, son mucho más grandes de aquello que pueda resultar de alguna utilidad en nuestra existencia en el mundo físico sensible en el que nos desenvolvemos, teniendo siempre claro que por inmensos e inconcebibles que sean estos números, no son, ni en atisbo, comparables con aquello que nuestra humanidad ha querido visualizar con el infinito, aquel que es únicamente alcanzable en potencia y con el uso de nuestras facultades mentales más abstractas.

 

---

Fuente de imágenes :

[ 1 ] Imagen editada por Vinicio Barrientos Carles     

[ 2 ] Imagen editada por Vinicio Barrientos Carles    

[ 3 ] Imagen editada por Vinicio Barrientos Carles    

[ 4 ] Imagen tomada de gAZeta, editada por Vinicio Barrientos Carles     

[ 5 + 7 + 8 ] Imágenes elaboradas por Vinicio Barrientos Carles

[ 6 ] Imagen editada por Vinicio Barrientos Carles