Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
La entropía es el precio de la estructura.
Erwin Schrödinger
La palabra entropía proviene del mismo vocablo, en griego antiguo, significando transformación o evolución. Operacionalmente, se trata de una magnitud física extensiva de un sistema aislado, una función de estado, que describe ciertas características de su evolución, considerándose conceptualmente uno de los pilares fundamentales en la ciencia contemporánea, abarcando aspectos de la física, la química y la biología, así como de otras ciencias más específicas como la ecología y la psicología social, por mencionar unas, a manera de ejemplo.
En este sentido, cabe apuntar que se trata de un concepto que ha emergido de manera gradual desde áreas muy diversas, destacando entre ellas la termodinámica, la mecánica estadística, la teoría de la información, pero más recientemente desde la teoría de la organización. También es oportuno mencionar que este proceso, para su correspondiente maduración, ha tomado su tiempo, abarcando los dos últimos siglos. Por otro lado, el concepto encierra un inherente carácter holístico, por lo que dentro del pensamiento transdisciplinar ha adquirido nuevos brillos, en lo que respecta a los avances de las últimas décadas, en especial respecto a la relevancia de la segunda ley de la termodinámica en el ámbito cosmológico.
De manera coloquial, suele presentarse a la entropía como una medida del desorden del sistema en cuestión, es decir, del desorden en el que se encuentra cuanto lo compone. Al hablar de orden o desorden tendremos que apuntar, de manera no evitable, a la noción de estructura del sistema. De esta guisa, se tiene que, a una mayor entropía mayor será el desorden. Sin embargo, la palabra desorden no explica por sí misma a qué exactamente nos estamos refiriendo. Es decir, aunque pueda resultarnos intuitiva, podría presentar ambigüedades insalvables y no admisible para el rigor científico deseable, por lo que varias propuestas se han ido planteando, a lo largo del tiempo, para precisar su comprensión.
Previamente, en este Suplemento Cultural LaHora, hemos mencionado a la entropía en el artículo «La flecha del tiempo: introducción», a propósito de su importancia en la definición del discurrir físico del tiempo, asociado a la irreversibilidad de ciertos procesos fisicoquímicos, lo que implica una direccionalidad natural del tiempo. En este artículo se recurrió al enunciado termodinámico fundamental, la segunda ley, o segundo principio, que establece, en palabras llanas, que todo proceso termodinámico nunca deriva en un decrecimiento de la entropía. Simbolizada por la letra S, el enunciado matemático correspondiente es, simplemente: dS ≥ 0. Respecto al planteamiento y evolución del concepto, se lee.
Se propone una función de estado llamada entropía, simbolizada por S, por lo general asimilada a la noción de aleatoriedad del sistema, que no puede más que crecer en el curso de una transformación termodinámica real.
La segunda ley de la termodinámica es muy importante, porque, a diferencia de las otras leyes fundamentales de la física del cosmos, esta no es simétrica respecto a la variable tiempo. Esto significa, en otras palabras, que los procesos físicos no son naturalmente reversibles, aunque algunos parezcan serlo, lo que redunda en un transcurrir del tiempo siempre «hacia adelante». Sobre la ley se encuentra:
Es un principio de la evolución que fue enunciado por primera vez por Sadi Carnot en 1824. Después ha sido objeto de numerosas generalizaciones y formulaciones sucesivas por Clapeyron (1834), Clausius (1850), Lord Kelvin, Ludwig Boltzmann en 1873 y Max Planck (consúltese la historia de la termodinámica y la mecánica estadística), a lo largo del siglo XIX y hasta el presente.
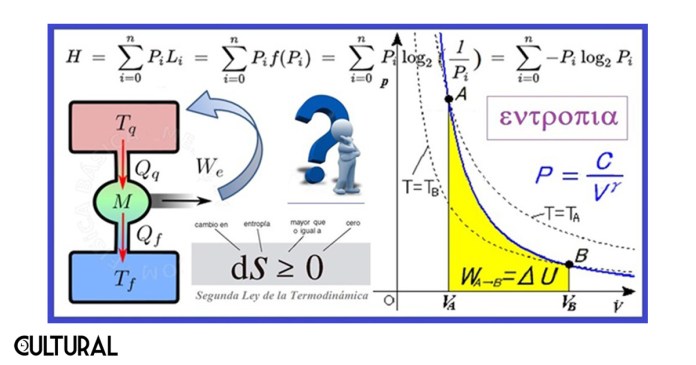
En la imagen precedente, tomada del artículo sobre la flecha del tiempo, se ilustra un poco de la historia del principio termodinámico y de su correspondiente descubrimiento. Al revisar, justamente, la evolución del concepto de entropía, puede concluirse que las ideas originarias del mismo se remontan a inicios del siglo XVIII, cuando se observa, de manera sistemática, que las cantidades de energía liberada en las reacciones de combustión producen siempre una disipación de la misma, mediante el calor o la fricción, de manera que esta energía perdida no se transforma en ninguna forma de trabajo mecánico útil.
En este contexto, de la ingeniería de máquinas, se persiguió alguna forma de minimizar esta disipación energética, maximizando la eficiencia del sistema mecánico. Empero, los esfuerzos resultaron infructuosos, pues la búsqueda de la máquina perfecta fracasó. Cierto es que, de todas las investigaciones realizadas sobre esta pérdida de energía, aparentemente inevitable, Rudolf Clausius, físico y matemático alemán, destacó al concluir que, en cualquier sistema termodinámico real, siempre se daría lugar a lo que él denominó procesos irreversibles, durante los cuales cierta cantidad de energía se escapaba en forma de calor, de una forma lenta y gradual, a través de las fronteras del sistema.
Clausius formalizó matemáticamente sus ideas y publicó en 1850 su obra cumbre al respecto de la teoría mecánica del calor, en la cual se estableció por primera vez el enunciado formal de la que hoy conocemos como la segunda ley de la termodinámica. Quince años después Clausius acuñó el término entropía, con el cual la formulación del citado principio dice así: «La cantidad de entropía del universo tiende a incrementarse en el tiempo». Véase en la imagen siguiente un mapa conceptual de la interdependencia de las ideas generadas a partir de ese momento, el cual refleja la dispersión, a la vez amplitud, de la noción. Como veremos, llega hasta nuestros días en formas totalmente insospechadas.
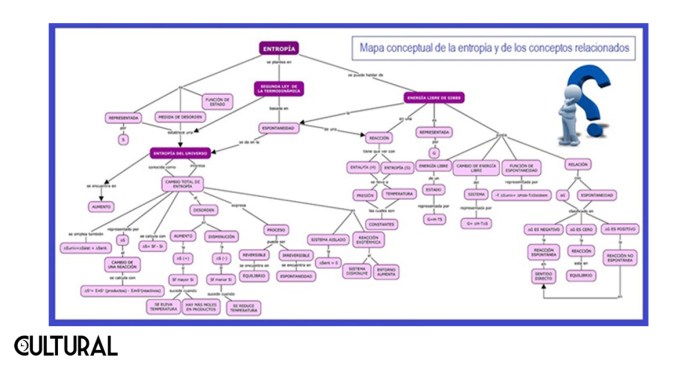
El concepto de proceso termodinámico reversible es muy importante. De una manera muy simplificada, un proceso es reversible si es posible llevar al sistema desde un estado inicial hasta otro final, de tal forma que pueda posteriormente retornarse al estado inicial mediante un proceso inverso. Vale anotar que estos procesos son justamente ideales, en uno o en varios sentidos, puesto que, a decir verdad, la entropía se mantendrá constante respecto de niveles de medición bastante aproximados, que para fines prácticos implican un cambio cero.
No obstante, en rigor, para que el cambio en la entropía fuera efectivamente nulo se necesitaría de un tiempo infinito, para que los infinitos estados intermedios implicaran un equilibrio termodinámico real. Empero, es usual considerar algunas idealizaciones que implican disipación energética cero, o casi, casi cero, como cuando se imagina una superficie totalmente lisa, sin fricción alguna, cosa que en la práctica sabemos que es realmente imposible. Otros ejemplos son la elongación de un resorte o material elástico, dentro de sus límites de tolerancia, y el cambio de estado físico de un material, como una cantidad de agua que pasa de sólida a líquida y viceversa. Otros casos se muestran en la imagen que sigue.
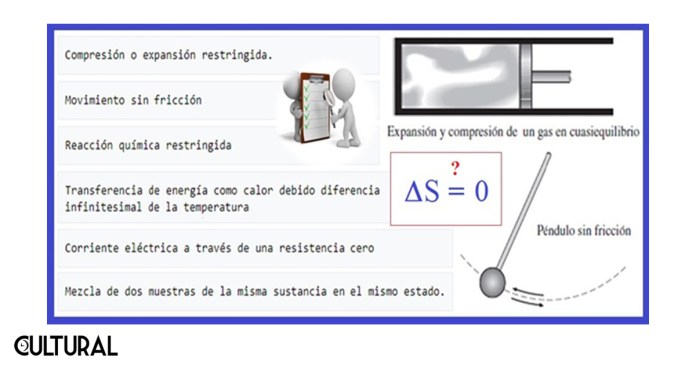
A pesar de estas abstracciones, el principio que subyace en la segunda ley de la termodinámica establece cabalmente la irreversibilidad de todos los fenómenos físicos, especialmente durante el intercambio de calor, de forma tal que la noción de desorden (entropía) no puede más que crecer en el curso de una transformación termodinámica real y de largo plazo. Esto está vinculado con fenómenos que, por cotidianos, pasan desapercibidos, asimilándolos al «sentido común» de nuestras observaciones.
Para ilustrar el asunto, reflexionemos sobre el siguiente caso. Cuando accidentalmente soltamos un pichel de vidrio con refresco, caerá, y al golpear el piso posiblemente se romperá y el refresco se esparcirá por el suelo. Nunca veremos reintegrarse los pedazos de vidrio reconstruyendo el pichel, ni el refresco retornando al envase que originalmente lo contenía; tampoco veremos que los cuerpos que han caído retornen a sus puntos de partida. Lo que establece la segunda ley de la termodinámica es precisamente que todos los sistemas en el universo tienden en su conjunto a volverse más desordenados, más dispersos, más homogéneos y de ahí las transferencias de calor.
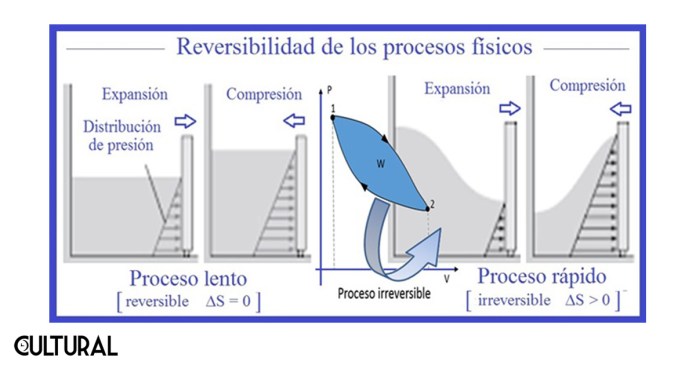
Hasta ahora hemos anotado algunas ideas provenientes de la termodinámica originaria, que en su totalidad conduce a la noción de un desorden creciente a todo nivel, incluyendo el atómico, y sobre cómo una gran cantidad de energía útil se disipa y se pierde en lo que parecería un estado de aleatoriedad inconmensurable. Sin embargo, hemos comentado que el concepto de entropía aparece en otros contextos, como el estadístico y el referido a la información.
En este último aspecto, esta cuantificación del desorden se traducirá en una medida de la incertidumbre y de la información necesaria para que, en cualquier proceso, se pueda acotar, reducir o eliminar esta incertidumbre. De esta forma que el concepto de información y el de entropía (de Shannon, en honor al matemático Claude Elwood Shannon) resultarán básicamente relacionados entre sí, aunque es importante recalcar que se necesitaron muchos años de desarrollo de la mecánica estadística y de la teoría de la información para que esta íntima relación pudiera ser establecida con total claridad.
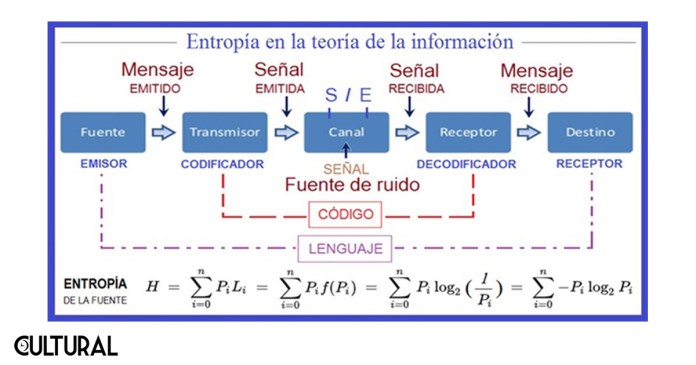
En cierto sentido, entropía e información son dos conceptos opuestos, lo cual es más claro cuando se piensa en términos de la estructura que existe en un sistema o entidad. De ahí el titular de nuestro artículo de esta oportunidad. En términos simples, a mayor estructura se tiene menos homogeneidad, y así menor entropía; por otro lado, de manera conversa, cuando pensamos en el incremento de la homogeneidad o uniformidad de un sistema o entidad, veremos que la información que el sistema contiene disminuye. Esto significa que la entropía y la información están en una relación inversa.
Así, como sucede en el ejemplo del pichel que cae, al dejar caer sobre un cesto un conjunto de limones, estos se repartirán de forma tal que la entropía del sistema aumente al máximo, reduciendo la información contenida en esta distribución, tendiendo siempre a la más uniforme posible. La concentración y el arreglo, de acuerdo a cierta estructura, implica una mayor información en el sistema. La heterogeneidad va de la mano con la información, lo que es contrario a la aleatoriedad o entropía. Nunca los limones caerán de forma tal que adopten la forma de un arreglo cúbico, por ejemplo, puesto que la entropía se reduciría, aumentando la información (estructura) del nuevo arreglo.
Conviene retomar estas ideas, recurriendo al concepto de neguentropía, pero, en particular, en el caso de los seres vivos, como se menciona en la cita inicial del físico austriaco Erwin Schrödinger. En los organismos biológicos, la evolución y otros procesos emergentes implican organización, no desorden. La vida implica un grado de estructura que se sostiene y no se degrada, no se desordena. Los sistemas en el interior de un organismo se autosostienen y se regeneran. Es la autopoiesis. En esta línea de pensamiento, traer a colación una de las citas más notables de Schrödinger: «Un organismo vivo produce entropía positiva y por ello tiende a aproximarse al grado de entropía máxima, que es la muerte. Para evitarlo, se alimenta».
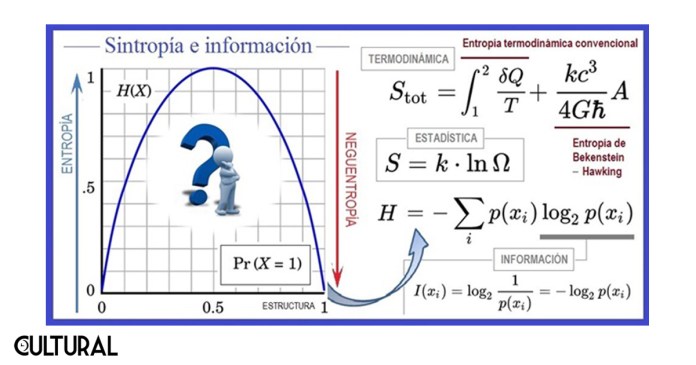
Norbert Wiener, el matemático estadounidense fundador de la cibernética, escribió en algún momento que, así como la entropía mide el grado de la desorganización de un sistema, la información, que suministra un conjunto de mensajes, es una medida de la organización del mismo. Esto lo sintetiza muy bien el físico y sistémico de origen ruso, nacionalizado belga, Ilya Prigogine, al aseverar que la entropía siempre tiene dos elementos dialécticos: un elemento creador de desorden, y otro complementario, creador del orden, de forma tal que la inestabilidad, las fluctuaciones y la irreversibilidad desempeñarán un papel fundamental en la evolución del cosmos.
De esta guisa, que el incremento de la entropía se transforma en un indicador efectivo de la evolución espontánea del sistema, traduciéndose en la física basal para el establecimiento de una flecha del tiempo, como hemos mencionado más arriba. Como estamos insistiendo, el concepto de entropía fue desarrollado desde diferentes perspectivas, con trabajos académicos ciertamente independientes, impulsados por verdaderos pioneros que supieron imprimir originales innovaciones a la ciencia de su momento. Empero, integrando y simplificando esta evolución, podemos sintetizar, los siguientes tres momentos, en orden cronológico:
- a) La termodinámica, con el físico y matemático alemán Rudolf E. Clausius, en 1850.
- b) La mecánica estadística, con el físico austriaco Ludwig E. Boltzmann, cerca de 1900.
- c) La teoría de la información, con el matemático e ingeniero eléctrico norteamericano Claude E. Shannon, en 1948, cuando publicó Una teoría matemática de la comunicación, que supuso un hito después de sus contribuciones con trabajos sobre el descifrado de códigos y la seguridad en las telecomunicaciones.
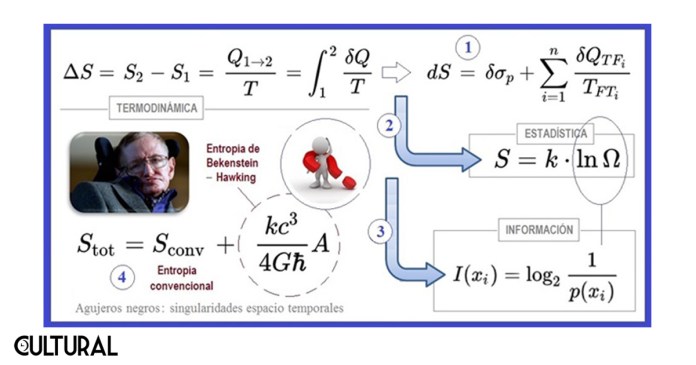
Existe una cuarta contribución, en el campo de la física cosmológica, liderada en gran parte por el astrofísico británico Stephen Hawking, que hemos mencionado en el artículo «Horizonte de sucesos», en la columna Episteme, a raíz de los aportes del teórico en el desarrollo de una para la entropía del sistema constituido por los objetos que engulle un agujero negro, en las fronteras de la superficie de su horizonte de sucesos, la cual desentrañó la relación existente entre la entropía termodinámica física y la entropía de Shannon en la teoría de la información, dos conceptos que habían coexistido de manera independiente y sin una conexión explícita.

Según la nueva teoría de Stephen Hawking y Jacob D. Bekenstein, de 1978, el bit de información sería equivalente a una superficie de valor un cuarto del área de Planck. Específicamente, en las fronteras de un agujero negro, la segunda ley de la termodinámica, solo puede cumplirse si se introduce un término extra que depende del área total (A) de todos los agujeros negros existentes en el universo, como se muestra en las dos imágenes previas.
Sumarizando, el concepto de entropía aparece en la historia de la ciencia para la pertinente formalización de la citada segunda ley de la termodinámica, que establece que el valor de la entropía del universo no puede decrecer, lo que implica que el desorden de todos los sistemas en su conjunto deberá indefectiblemente aumentar, convirtiendo al cosmos en uno cada vez más uniforme, más disperso, más homogéneo y más frío. Si la energía no puede crearse ni destruirse, la entropía total en un sistema cerrado solo podría permanecer casi constante, si se tratara de un caso ideal conformado únicamente por procesos reversibles, lo cual es imposible por todos procesos físicos con algún grado de irreversibilidad.
Complementariamente, no puede dejar de hacerse mención y de ponderarse las contribuciones del físico y filósofo austriaco Erwin Schrödinger, el mismo del famoso gato, ganador del Premio Nobel de Física en 1933, en forma compartida con Paul Dirac, por su contribución a la mecánica cuántica con la ecuación epónima que lleva su nombre. En particular, resulta que, en 1944, el físico austriaco publicó un pequeño texto titulado «¿Qué es la vida?» (What is life?), obra que influyó grandemente en la biología de la segunda mitad del siglo XX. De hecho, la cita previa que hemos realizado del notable teórico está tomada de este breve, pero substancial libro.
En este sentido, sus dos aportes principales están relacionados con el concepto de entropía, de la siguiente manera:
- a) La vida no es ajena a las leyes de la termodinámica, pero debe apuntarse que los sistemas biológicos conservan su complejidad exportando la entropía que producen sus procesos, lo cual implica la existencia de otros procesos adicionales de autorregulación energética que estructuran el sistema (que en términos actuales implican la neguentropíadel mismo).
- b) La química de la herencia biológica debe basarse en un cristal aperiódico, lo cual contrasta con la periodicidad exigida a un cristal capaz de codificar información necesariamente irregular (que es otra vertiente del concepto de la neguentropíapara la autoestructuración de los sistemas biológicos).
Esta neguentropía, también llamada entropía negativa o sintropía, es la entropía que el sistema exporta para mantener su entropía en valores bajos. Es decir que, para compensar el proceso de degradación sistémica a lo largo del tiempo, algunos sistemas abiertos consiguen compensar su entropía natural con aportaciones de subsistemas con los que se relacionan. En cierta forma, la irreversibilidad propia de un sistema cerrado se traduce en una secuencia entrópica que no puede detenerse por sí sola, mientras que, en un sistema abierto, como el caso de uno biológico, la neguentropía pasaría a ser una modalidad de resistencia sustentada en subsistemas vinculados que reequilibran el sistema entrópico basal.
La provisión energética proveniente de procesos biológicos, tales como la respiración y la alimentación, o la fotosíntesis basal en las plantas, son ejemplos de estos subsistemas eficientemente incorporados. De esta forma, los seres vivos, como sistemas, no responden a la conducta esperada por un sistema termodinámico estándar, puesto que su metabolismo y la cibernética asociada se encargan de proveer energía, organizando las estructuras y subsistemas, e inclusive intercambiando información con el ambiente, modificándolo para su conveniencia.
Conviene ahora recordar las cuatro características de un sistema complejo: autoorganización (emergencia), no linealidad (caos), adaptación (cibernética) y conectividad (redes). Así, lo establecido por la segunda ley de la termodinámica se cumple a nivel global, pero para muchos subsistemas componentes, de manera temporal, se tendrá una conducta opuesta, con tendencia a la organización y la creación de niveles más elevados de información. Esta es, en efecto, una característica esencial de lo que denominamos «vida», que, como sabemos es necesariamente temporal, finita y acotada para cualquier organismo del que se trate.
El biólogo y filósofo austríaco Karl Ludwig von Bertalanfly, reconocido fundamentalmente como el padre de la teoría general de sistemas, expresa, con relación a la neguentropía, como medida del orden o la estructura de un determinado sistema, lo siguiente:
Esta medida de la información resulta ser similar a la de la entropía, o más a la de la entropía negativa, puesto que la entropía es definida como logaritmo de la probabilidad. Pero la entropía, como ya sabemos, es una medida del desorden de ahí que la entropía negativa o información sea una medida del orden o de la organización, ya que la última, en comparación con la distribución al azar, es un estado improbable.
La cita está tomada de su obra «Teoria general de los sistemas», publicada en 1968. En todos estos aportes y avances teóricos existe una referencia subyacente ineludible a los fenómenos de la complejidad, los cuales han ido cobrando mayor fuerza a partir de las crisis generalizadas de la ciencia y de la filosofía, acaecidas en las primeras tres décadas del pasado siglo XX, los cuales hemos citado como inicio para un nuevo Renacimiento, un cambio de macroparadigma, una nueva supercultura de carácter epistemológico universal.
Un último aporte se ha venido a sumar a esta interrelación de conceptos. Se trata del desarrollo de una teoría matemática que estudia los mecanismos de formación de las estructuras disipativas, a partir de reacciones caóticas de no equilibrio, para restaurar las cadenas de simetría rota con una nueva estructura ordenada, lo cual incluye la ruptura en la simetría temporal por la distinción unidireccional entre el pasado y el futuro, determinada por la flecha del tiempo.
Esta teoría matemática es la teoría de la información, en la cual, la entropía de Shannon (información), la neguentropía biológica (sistemas complejos) y la entropía global del cosmos (termodinámica) implicarían la existencia de un único concepto en construcción, en torno de la simetría-estructura, global y local, de los sistemas en el universo. El estudio de la entropía es parte esencial de estas nuevas disciplinas holísticas, incluida la cibernética, fundamentadas en el nuevo paradigma de la complejidad, como superación del paradigma monodisciplinario de la Modernidad. Estos conceptos, interesante de por sí, se encuentran en plena cimentación y desarrollo.
Fuente de imágenes:
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: https://lahora.gt/lh-suplementos-culturales/culturalahora/2023/03/03/la-flecha-del-tiempo-introduccion/
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/Entrop%C3%ADa
[ 3 ] Imagen editada por Vinicio Barrientos Carles :: http://lasegundaleydelatermodincamica.blogspot.com/2016/11/procesos-reversibles-e-irreversibles.html + https://es.wikipedia.org/wiki/Proceso_reversible
[ 8 ] Imagen editada por vbc :: https://www.scoopnest.com/es/user/Ntelevisa_com/974089741523210240-y-este-es-el-mensaje-que-eligio-como-epitafio-el-cientifico-la-hrefessstephen-hawkingglugstephen-haw + https://tn.com.ar/internacional/el-mensaje-que-eligio-stephen-hawking-para-su-lapida_856737
[ 4 + 5 + 6 + 7 + 9 ] Imágenes elaboradas por Vinicio Barrientos Carles








