Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
… parecía realmente pertenecer a la geometría, pero estaba dispuesto de tal manera que ni precisaba la determinación de cantidades ni admitía solución mediante el cálculo de ellas, no dudé en referirlo a la geometría de la posición
Leonhard P. Euler
La idea de que la Matemática es un asunto de números es una idea errónea y ciertamente nociva para una pertinente y fructífera integración social de los profesionales de esta ciencia formal, y más aún en una sociedad fuertemente necesitada de los servicios y aportes que estos científicos pueden realizar. En esta visión, un tanto deformada del quehacer matemático, mucho tiene que ver, sin lugar a dudas, el fallido sistema educativo, que ha terminado operacionalizando las actividades de aprendizaje, a tal punto que se ha perdido de una manera paulatina el meollo formativo del porqué las distintas disciplinas que integran el currículo escolar son importantes en los procesos de construcción mental, tanto cognitivos como emocionales y de otra índole.
Es así como, a lo largo de los años, me he topado con una gran cantidad de funcionarios en las distintas universidades de nuestro país que no tienen la más mínima idea sobre para qué puede ser útil un matemático, es decir, en qué podría trabajar. Usualmente se piensa que son personas que únicamente pueden enseñar lo que saben, es decir, «dar clases de Matemática», cayendo en un círculo vicioso sin fin. Pero quizá sea otro día cuando nos entretengamos con esta problemática, y por ahora que nos baste recalcar que no es como se piensa: la Matemática no es solo cuestión de números.
Por otro lado, en estos días de crisis, la superada pandemia trajo a colación cómo en varios países del primer mundo, los institutos y las universidades más prestigiosos colocaron en la voz de sus departamentos de Matemática las recomendaciones respecto a lo que los modelos prospectivos decían al respecto de la evolución del brote. De repente, el mundo sentía curiosidad al respecto del aparecimiento de estos profesionales, que en el imaginario deberían estar frente a un pizarrón dando clases, atormentando a sus estudiantes, como es usual, con cosas del todo inútiles y, que en aquellos entonces de los tiempos pandémicos, se aparecían como relevantes para expresarse sobre lo que acontecía en el mundo, algo asombrosamente útil.
De esta guisa, la frase «modelos matemáticos» se volvió, de repente, coloquial. Medio mundo empezó a mencionar los modelos matemáticos. Sin embargo, nuevamente se trataba de modelación cuantitativa, lo que implicaba variables, cálculos… y números. A pesar de esta insistente (y reducida) noción, es importante rescatar que también existe, en el mismo imaginario, la idea de que los matemáticos son gente un tanto diferente a la que le gusta pensar, y podemos fácilmente asociarlos con ciertos entretenimientos o pasatiempos en los que, justamente, hay que pensar, unos en los que «se usa la lógica».
La noción anterior, aunque imprecisa, resulta mucho más acertada y próxima a lo que la Matemática viene siendo, la cual deberíamos concebirla como una disciplina relacionada con actividades como los juegos de salón y otro tipo de juegos basados en reglas, en la reflexión y estudio de las reglas que estos juegos utilizan para su buen funcionamiento, más que con la operatoria característica y propia de los cálculos. Después de todo, hoy por hoy, para eso están las computadoras y las distintas herramientas y paqueterías algorítmicas, que, en definitiva, nos han superado en este tipo de actividades.
![] Imagen tomada de gAZeta por Vinicio Barrientos Carles](https://lahora.gt/wp-content/uploads/sites/5/2023/05/6-Cult-2-2.jpg?w=696)
Por otro lado, cabe hacer mención que fue hasta hace poco menos de dos siglos que se inició un profundo cambio en la visión que los constructores líderes del edificio matemático tuvieron de este. Este cambio dio inicio con el denominado problema de las geometrías no euclidianas, estudiado de forma simultánea e independiente por varios matemáticos, entre los que destacan el alemán Carl Friedrich Gauss, el ruso Nikolái Lovachevski y el húngaro János Bolyai, y posteriormente el alemán Bernhard Riemann.
En forma muy resumida, tras la búsqueda de una posible redundancia del quinto postulado de la geometría planteada en los «Elementos» de Euclides, se encontró que, al negar este postulado, no solo ninguna contradicción aparecía, sino que era posible considerar otros tipos de sistemas geométricos igualmente consistentes que el original, de forma que era factible considerar, lógicamente, la existencia de distintos «mundos» sometidos a conjuntos diferentes de axiomas. Fue aquí donde despegó la característica abstracta de la Matemática, inclusive de la misma Lógica, de manera que la relación ontológica entre los objetos formales y los seres factuales (cosas de la realidad física sensible) cambió, básicamente porque los primeros son libres respecto de los segundos y pueden ser diseñados arbitrariamente una vez se apeguen a determinada consistencia lógica relativa a las reglas de construcción.
En suma, con este despegue hacia la abstracción, los sistemas formales se independizaron y la Matemática en la actualidad es visualizada como una colección de disciplinas, o áreas, dedicadas al estudio de cierto tipo de sistemas o estructuras formales, las cuales pueden ser aplicadas en distintos contextos y que responden a determinados tipos de problemas «matemáticos». El hecho es que el crecimiento de la Matemática en el último siglo no tiene parangón con ninguna otra ciencia, habiendo crecido, según lo estiman los especialistas, en un factor mayor a veinte. Esto significa que, si el saber matemático acumulado hasta antes de los inicios del siglo XX ocupaba, por decirlo así, un anaquel de resultados y teoremas, este cúmulo es al día de hoy de más de veinte anaqueles. Para completar este asombro, anótese que los estudios universitarios, con la excepción de los especializados en Matemática, abarcan menos de los conocimientos previos a los de mediados del siglo XIX.
Toda esta ciudadela de producción matemática se encuentra interconectada y ciertamente puede ser organizada en edificios (áreas o subdisciplinas). En este sentido, es interesante consultar la clasificación de la Matemática que la Unesco llevó a cabo hace ya cuarenta años. En esta, las ciencias formales aparecen primero, siendo la Lógica correspondiente al código 11 y la Matemática al código 12. Adentro del código 12, pueden verse las ciencias de la Computación con el código 1203, siendo plausible plantear actualmente una independencia de este campo de estudio, por lo que pasaría a constituirse en la tercera ciencia formal, pudiendo ser recatalogada con el código 13. En esta clasificación se pueden apreciar diez edificios, dentro de los cuales hay en total más de setenta habitaciones, siendo cada habitación una disciplina matemática. El título del artículo responde a uno de estos edificios, cabalmente el que codificado como 1210: Topología, del griego τόπος-topos, lugar y λόγος-logos, estudio.
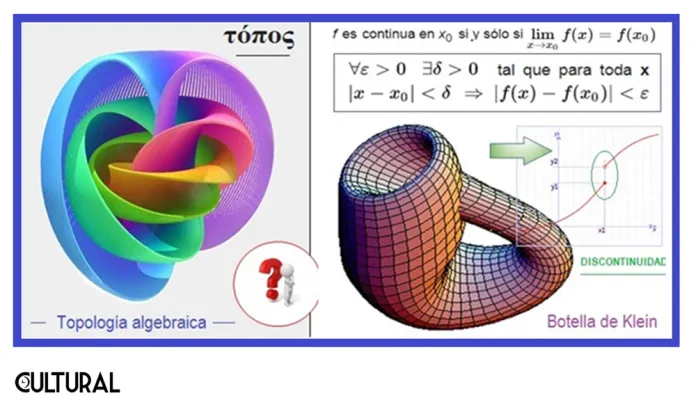
Para iniciar nuestra panorámica sobre la Topología, posiblemente nunca antes escuchada, quizá convenga citar al suizo Leonhard Euler, sin duda el matemático más brillante y prolífico del siglo XVIII, cuando hace referencia al tema en su solución del denominado problema de los siete puentes de Königsberg:
además de aquella parte de la geometría que trata sobre cantidades y que se ha estudiado en todo tiempo con gran dedicación, el primero que mencionó la otra parte, hasta entonces desconocida, fue G. Leibniz, el cual la llamó geometría de la posición. Leibniz determinó que esta parte se tenía que ocupar de la sola posición y de las propiedades provenientes de la posición en todo lo cual no se ha de tener en cuenta las cantidades, ni su cálculo (…). Por ello, cuando recientemente se mencionó cierto problema que parecía realmente pertenecer a la geometría, pero estaba dispuesto de tal manera que ni precisaba la determinación de cantidades ni admitía solución mediante el cálculo de ellas, no dudé en referirlo a la geometría de la posición.
Hemos iniciado señalando que la Matemática se concibe en la voz popular como la disciplina de «los números», lo cual viene a ser una fotografía, no solo parcial, sino bastante sesgada de lo que es el quehacer matemático. En particular, apuntamos que la construcción del edificio matemático ha sido una tarea histórica y acumulativa, pero no siempre lineal, proceso en el que han ido apareciendo nuevas áreas y subdisciplinas, mencionando a este respecto la clasificación que utiliza la Unesco. Así, por ejemplo, en esta codificación, el primer dígito 1 refiere a las ciencias formales, siendo 11 la Lógica y 12 la Matemática. Asimismo, dentro de cada una de estas primeras áreas científicas existen subdivisiones que utilizan los siguientes dos dígitos, completando así la clasificación de cuatro dígitos, que al ser completada con otra subdivisión más específica llega a la clasificación de seis dígitos. La conformación de la Matemática, código 12, aparece así:
1201 Álgebra
1202 Análisis y Análisis Funcional
1203 Ciencias de la Computación
1204 Geometría
1205 Teoría de números
1206 Análisis Numérico
1207 Investigación Operativa
1208 Probabilidad
1209 Estadística
1210 Topología
1299 Otras especialidades matemáticas
Por otro lado, enfatizamos sobre el gran despliegue y monumental crecimiento de la producción matemática del último siglo, la cual representa más del 95 % del total de resultados existentes al día de hoy. Queda claro que la educación y la difusión de estos nuevos conocimientos se ha quedado demasiado atrás, para ir al paso de lo que el gran público debería saber al respecto de a qué se refiere todo este cúmulo de saberes formales, tan importantísimos para el desarrollo de la ciencia en general.
También comentamos que fue en la Geometría en donde se gestó la mayor claridad para dar el salto fundamental, que convertiría a la Matemática en un todo ordenado de sistemas y estructuras formales abstractas, totalmente independientes de la realidad concreta, es decir, independiente de los planos físicos sensibles en donde existimos, los que eran frecuentes y usuales en los tiempos del matemático indio Brahmagupta. Aunque se encuentra una diversidad de enfoques para una posible división de la Matemática, todas las clasificaciones incluyen las muy conocidas áreas de la Aritmética (1205: teoría de números), la Geometría, el Álgebra, el Análisis (que incluye al Cálculo Integrodiferencial) y la teoría de la probabilidad, así como otras disciplinas afines, como son la Lógica, la teoría de la computación, la teoría de juegos y otras englobadas en las denominadas matemáticas aplicadas.
La Topología, identificada por la Unesco con el código 1210 es una rama poco conocida a nivel elemental. Si tuviéramos que sobresimplificar, podríamos aseverar que los sistemas matemáticos, y así los objetos en ellos, más allá de una fundamentación lógica, pueden poseer una naturaleza de tipo semántico que responde a una estructura numérica (aritmética o analítica), una estructura geométrica, una estructura algebraica o una estructura topológica, o, más exactamente, a una combinación de este tipo de estructuras. Al revisar nuestras nociones al respecto, caemos en la cuenta de que no poseemos una noción, aunque sea vaga, de lo que el calificativo «topológico» pueda significar, a diferencia de los otros tres, léase numérico, geométrico o inclusive eso de «lo algebraico».
Como indicamos, la palabra «topología» proviene de las raíces griegas τόπος, topos, que significa lugar, y la más conocida λόγος, logos, que traducimos como estudio, discurso o tratado. Así, la Topología vendría ser la disciplina matemática que estudia las propiedades espaciales o relacionales de los objetos matemáticos, y lo topológico se refiere a la estructura espacial más general. Si buscamos una definición, Wikipedia nos dirá que es el estudio de aquellas propiedades de los cuerpos que permanecen inalteradas por transformaciones continuas, lo cual no nos dice mucho, si no contamos con un concepto bien definido de lo que significa esto de «la continuidad». Para acercarnos a este concepto, regresamos nuevamente a la historia, recordando el problema que Leonhard Euler resolvió en 1736. Por ello le hemos incluido en nuestro epígrafe.
![] Imagen editada por vbc](https://lahora.gt/wp-content/uploads/sites/5/2023/05/6-Cult-4.jpg?w=696)
Esto trae a colación el tema de que, en contraste con el Álgebra, la Geometría y la teoría de números, mejor conocida como Aritmética, cuyas genealogías datan de tiempos antiguos, la Topología aparece mucho más recientemente. En la cita que hemos copiado de L. Euler, el matemático suizo explica que Gottfried Leibniz ha planteado anteriormente un tipo de análisis geométrico que no recurre a las cantidades y que tampoco depende de las distancias de los objetos en cuestión. Así, apenas en el siglo XVIII, el prolífico matemático rescata el título que Leibniz ha usado anteriormente, Analysis situs, es decir, análisis de la posición. Para la resolución del famoso problema de los siete puentes de Königsberg, Euler utiliza unas novedosas técnicas, las cuales pasarán con los años a dar origen a la moderna teoría de grafos.
El problema corresponde al caso real de la ciudad de Königsberg, en la antigua Prusia Oriental, ciudad que pasó después a ser parte de Alemania, y luego, desde 1945, se convertiría en la actual ciudad rusa de Kaliningrado. Resulta que la ciudad es atravesada por el río Pregel (Pregolia en ruso), el cual se bifurca para rodear con sus brazos a la isla Kneiphof, dividiendo el terreno en cuatro regiones distintas (en verde en la imagen precedente), las que entonces estaban unidas mediante siete puentes, según puede observarse en el diagrama. El problema consistía en encontrar un recorrido para cruzar a pie toda la ciudad, pasando solo una vez por cada uno de los puentes, y regresando al mismo punto de inicio.
La solicitud planteada en el problema resulta imposible, es decir, no existe ninguna posible ruta que satisfaga las características planteadas. Sin embargo, aunque el problema puede resolverse aplicando un «método de fuerza bruta», es decir, probando todos los posibles recorridos existentes, es notable que Euler desarrolló un método general con el cual demuestra una solución generalizada del problema, método que puede aplicarse a cualquier territorio en el que ciertos accesos estén restringidos a ciertas conexiones. Esto lo redacta brillantemente en Solutio problematis ad geometriam situs pertinentis.
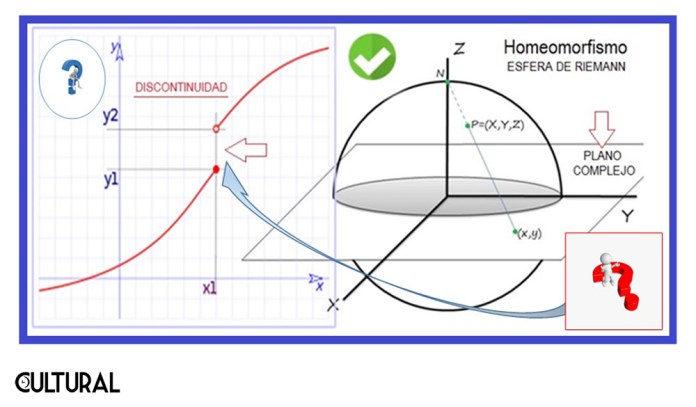
Los problemas topológicos se ocuparán de aquellas propiedades de las figuras que permanecen invariantes, cuando son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos o se hagan coincidir puntos diferentes. Esta matemática de la deformación extrema, como puede apreciarse al transformar «topológicamente» una taza en una dona (ver imagen siguiente), está basada en la noción de una transformación continua, la cual presupone y establece que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación producida por la transformación hace corresponder «puntos próximos» a otros «puntos próximos», que pasará a ser la noción intuitiva de esta característica de la continuidad. De hecho, cuando una transformación y su transformación inversa son ambas continuas estaremos hablando de un homeomorfismo, que no es más que la forma de preservar la estructura topológica de un determinado conjunto. Iremos dando oportuno cierre en la parte tercera.
![] Imagen editada por Vinicio Barrientos Carles](https://lahora.gt/wp-content/uploads/sites/5/2023/05/6-Cult-5.jpg?w=696)
La palabra o prefijo topo la asociamos generalmente con un animal subterráneo y con poca visión. Sin embargo, esta palabra proviene del latín talpa, siendo de hecho Talpidae la familia de los topos. Por otro lado, el prefijo topo, en las palabras topografía, toponímico y topológico, proviene de la raíz griega τόπος, que significa lugar. De esta forma, toponimia es el estudio de los nombres propios de los lugares y topografía se refiere a las características propias de un terreno. Por ello apuntamos que la Topología es una disciplina matemática que se encarga del estudio de aquellas propiedades de los sistemas que permanecen invariantes bajo transformaciones continuas, características que pasan a constituir la denominada estructura topológica de este espacio abstracto. Por otro lado, así como en las estructuras algebraicas se utilizan ciertos conceptos clave, usualmente expresados por medio de operaciones binarias, en los espacios topológicos (aquellos dotados de alguna estructura topológica) interesarán conceptos espaciales que resulten invariantes bajo continuidad, tales como los de proximidad, número de agujeros, tipo de textura, compacidad, conectividad y metrizabilidad, entre otros.
Conviene aclarar que la expresión «una topología», con minúscula inicial, refiere a una de las estructuras de tipo topológico que estudia la Topología, de igual forma que «un álgebra» es un tipo especial de estructura algebraica, que son el objeto de estudio del Álgebra, otra de las ramas de la Matemática. Aunque el topólogo considera los mismos objetos que el geómetra, lo hace de un modo ciertamente distinto: no se fija ni en las distancias ni en los ángulos, ni siquiera de la alineación de los puntos. Por ejemplo, para el topólogo un círculo es equivalente a una elipse, al igual que una esfera no se distingue de un cubo, desde el momento que puede ir de uno a otro mediante una transformación continua y totalmente reversible, esto es, mediante un homeomorfismo. Así, en la Topología, los cuerpos son tratados como si estuvieran hechos de una goma infinitamente elástica, que no implique ni quiebres ni «discontinuidades». Mire el lector en este enlace. cómo una taza y una dona (un toro) son topológicamente equivalentes, es decir, homeomórficos.
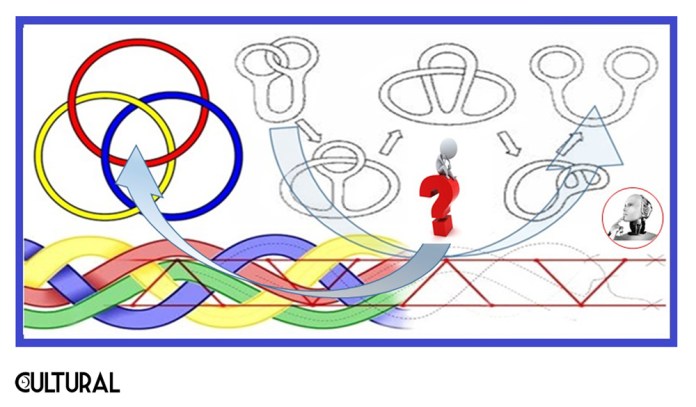
Estos conceptos de invariancia topológica, de preservación de cierta estructura espacial, tuvieron su historia, pero simplificando de sobremanera cabe mencionar los siguientes aspectos como cruciales:
- La teoría de grafos: con dos ejemplos clásicos: el problema de los siete puentes de Königsberg y el teorema de los cuatro colores, los cuales involucran en su resolución el desarrollo de complicados teoremas matemáticos (ambos problemas ilustrados en la primera parte del artículo).
- La teoría de nudos: con sorprendentes aplicaciones, entre otras, en la Biología Molecular y la Física. (Las nuevas formulaciones de la teoría de supercuerdas recurren a las variedades de Calabi-Yau, estrechamente relacionadas con lo incluido en un artículo previo sobre objetos multidimensionales).
- La teoría de superficies: en un sentido mucho más general que el geométrico estándar, en donde se clasifica la diversidad de tipos de superficies compactas.
La Topología es un campo reciente, pero vasto, cuyo desarrollo y evolución se encuentra íntimamente ligado al desarrollo abstracto de las matemáticas contemporáneas, por lo que aún una rápida revisión histórica resulta apasionante. Sin embargo, esta síntesis de los pasos fundamentales requeriría, siendo lacónicos, un par de publicaciones más. Aunque esto no es factible ahora, sí cabe señalar una distinción que desde el inicio quedó bastante asentada, y es la diferencia de enfoque para tratar los problemas que el original Analysis situs, desde G. Leibniz hasta H. Poincaré, vino a plantear. En efecto, el primero de estos autores, en 1679, publica su obra Characteristica Geometrica, en la cual pretende estudiar las propiedades topológicas, más que las puramente métricas, de las figuras, insistiendo que «se necesita de otro análisis, puramente geométrico o lineal, que también defina el situs (posición) como el álgebra define la magnitud».
Este enfoque moderno de la distribución de los puntos en el espacio con ciertas características que se conservan bajo cierto tipo de mapeos es justamente el rescatado por Euler de las ideas iniciales de Leibniz, el cual queda explícitamente manifiesto en su resolución del problema de Königsberg. Esta novedosa forma de tratamiento llevará a Euler al planteamiento de su famosa, pero muy simple fórmula: V – A + C = 2, la cual relaciona el número de vértices, aristas y caras de un poliedro cualquiera. La fórmula es compartida a su amigo Christian Goldbach en una carta de 1750. Poco después, el matemático suizo Simon Antoine Jean L’Huilier generalizará la fórmula así: V – A + C = 2 – 2g, en donde g es el número de «asas» o agujeros que posea el poliedro.
Lo interesante de esta cantidad que citamos es que se trata del primer invariante topológico de la historia. Este enfoque basado en la búsqueda de invariantes topológicos fue continuado profusamente por matemáticos teóricos de la talla del polímata y genial Henri Poincaré, quien introduce el concepto de homología y da una definición precisa de los denominados números de Betti, asociados a la topología de un espacio. Poincaré también introducirá el concepto de grupo fundamental de una variedad y la noción de homotopía, básicos en la denominada Topología Algebraica.
A pesar de lo complejo que pueda parecer el objeto de estudio de estas ramas matemáticas, los problemas provienen por lo usual de la formalización rigurosa de otros mucho más simples, a los que no podemos dar una explicación satisfactoria. Como ejemplo, tómese el problema de los cuatro colores, el cual establece que «dado cualquier mapa geográfico con regiones continuas, este puede ser coloreado con cuatro colores diferentes, de forma que no queden regiones adyacentes con el mismo color». Dicho de otra manera, nunca se requerirá de más de cuatro colores distintos para que el mapa no confunda las diferentes regiones. Este teorema ha sido probado ya, después de más de 120 años de luchas por su demostración, usando ordenadores electrónicos, lo que ha dado lugar a una serie de polémicas al respecto. Valdrá retomar esta problemática en una próxima y exclusiva ocasión.
Un segundo camino en el cual se desarrolla la Topología es por medio de la generalización de las ideas de convergencia, las cuales fueron originadas desde los tiempos antiguos, con la crisis de los inconmensurables de los pitagóricos y con el método de exhaución de Arquímedes. El proceso de construcción del concepto de límite también tiene su historia, abstrayendo la idea desde la noción de convergencia de una sucesión y dando por resultado una definición mucho más allá de los espacios métricos de Maurice Fréchet, llegando finalmente a Felix Hausdorff, quien presentó la primera definición de un espacio topológico abstracto en general. Con esta estructura será posible definir rigurosamente lo que significa la continuidad de una función, de donde podrá establecerse el concepto de homeomorfismo y de equivalencia topológica, fundamentales en la denominada Topología General o conjuntista. En la imagen última se muestra cómo la proyección estereográfica establece un homeomorfismo entre dos espacios topológicos equivalentes: la esfera de Riemann y el plano complejo extendido, que incluye el punto del infinito.