Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Para entender la recursividad, primero hay que entender qué es la recursividad.
Las diversas noticias sobre los avances de la IA, pero especialmente las referidas a aquellas nuevas herramientas que hacen evidente la capacidad que actualmente exhiben, en tareas antes reservadas exclusivamente para los seres humanos, han tenido un impacto, ciertamente, abrumador. Escuchamos, por todos lados, y de gente que no lo imaginaríamos, alguna que otra inquietud o comentario al respecto. En suma, múltiples factores han derivado en un despertar de las consciencias, en torno de algo que se había venido anunciando desde décadas atrás, tanto por teóricos, disciplinarios en una variedad de contextos, como por pensadores holísticos, ante una transformada y cambiante contemporaneidad. Obsérvese, como ejemplo, que ahora ya no es necesario aclarar a lo que nos referimos por IA.
Posiblemente son las generaciones más jóvenes, las que, encerradas en un conflicto de comunicación con las generaciones más experimentadas, reparan en una acertada crítica sobre lo desactualizado de las visiones y lo inverosímil que puedan resultar los consabidos consejos que los mayores pretenden dar. Por otro lado, estos últimos, habiendo superado una serie de obstáculos con la emergencia tecnológica de la segunda mitad del siglo pasado, se sienten en la calidad moral que la tradición les otorga, expresando su opinión como orientadora, desvelando en ese proceso su preocupante ignorancia frente el desconocimiento sistemático sobre cómo funciona realmente, en última instancia, nuestra compleja actualidad.
Por ello, en el artículo «Absolutismo, relativismo y actualidad» hemos descrito las ideas generales en torno de un cambio de macroparadigma, y el consecuente establecimiento de una supercultura diferente a la dominante en la Modernidad, a saber, una relacionada con el imperio tecnológico y la tecnocracia, basada en el denominado régimen de la información. Concluimos que el primer paso a dar es enterarnos de ciertas bases computacionales, en vista de que los sistemas educativos elementales se encuentran ya imposibilitados para actualizarse conveniente y pertinentemente. Así, caímos en la interrogante ¿qué es un algoritmo?, y aunque ya hemos incluido un ejemplo ilustrativo, nos encontramos transitando un camino de aproximaciones sucesivas, orientado a la ampliación de nuestros saberes en esta temática.
En la publicación «Expectativas y realidades del ChatGPT», en este mismo espacio para el conocimiento crítico y la cultura, apuntábamos, sobre los algoritmos, lo siguiente: «son procesos efectivos que pueden realizar acciones complejas, las cuales obedecen, por lo general, a una lógica recursiva […] La recursividad es otro tema que deberemos expandir, puesto que guarda, en su esencia, la naturaleza algorítmica». De allí que, hoy justamente, de manera rápida, estamos tratando de responder a ese particular punto. Nuestro epígrafe, un tanto en broma, hace referencia a lo que, en esencia, significa la recursividad: una llamada a sí mismo, esto es, una autorreferencia. Un proceso será recursivo si utiliza funciones que se llaman a sí mismas (denominadas recursivas).
Con un poquito de mayor rigor, una definición es recursiva si hace uso del concepto que está definiéndose, lo que parecería redundante o imposible. Sin embargo, para no generar un ciclo infinito que nunca termina, de llamadas a sí mismas, el proceso es tal que conlleva un caso límite, en que la llamada autoreferencial termina, y conduce a un caso ejecutable, denominado caso base. Lo mejor será ejemplificar e ilustrar la idea. No obstante, antes, enfatizar que hemos descrito un algoritmo como un proceso efectivo conformado de otros más simples, que son ejecutables con las condiciones primarias del agente algorítmico. Por eso en el párrafo previo usábamos la expresión acciones complejas.
Básicamente, un algoritmo siempre puede «descomponerse» en procesos más simples, o elementales. Sin embargo, aunque todo autómata o computador posee una cantidad finita de procesos elementales, la gran potencia de un algoritmo, bien diseñado, altamente efectivo, no proviene de su conformación, o descomposición, en procesos componentes más simples, sino de la característica que estamos mencionando, puesto que, en algún momento, todo algoritmo realizará llamadas recursivas, las que no consumen mayor diseño basal de la máquina, pero son capacitantes para que el algoritmo atienda un número elevadísimo, arbitrario, de casos o ejemplares de resolución.
En otras palabras, el algoritmo se autollama indefinidamente, corre, hasta que encuentra un caso soluble mediante un proceso elemental. Esta capacidad de hacer llamadas iteradas al mismo proceso básico, entiéndase, un inmenso número de veces, es la que proporciona al autómata finito una capacidad virtualmente infinita. Si el algoritmo corre a altas velocidades, y se dispone del suficiente tiempo y espacio para leer-escribir los movimientos parciales, el autómata o computador realizará tareas que un humano no podría realizar en ese mismo tiempo, dando la impresión de una mente operativa muy eficiente, y eficaz, claro está.
En términos generales, cualquier autorreferencia iterada es inherentemente recursiva, propiedad que se constituye en la potencia de cualquier proceso computacional, pues con pocos elementos (algoritmos) de base, es posible realizar muchas combinaciones que se iteran indefinidamente. En la imagen siguiente, se aprecia un par de estructuras fractales, un fragmento de código de un programa, y la ecuación logística discreta, todos objetos intrínsecamente recursivos.
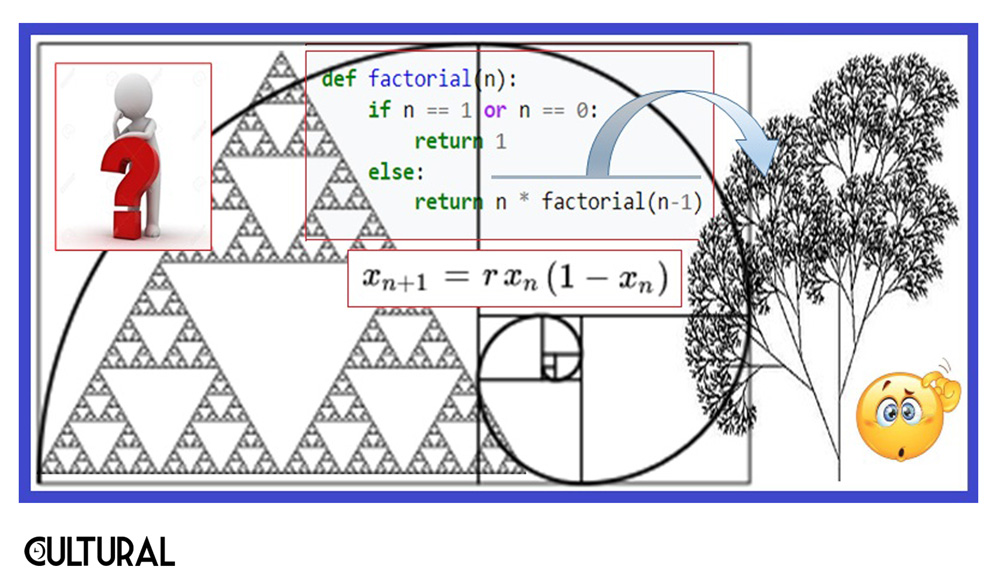
Colocaremos ahora un par de ejemplos ilustrativos, para concretizar la idea, finalizando con algunos comentarios de cierre al respecto. El primer caso es uno que hemos venido dejando entre líneas, en artículos previos, y hace referencia a un asunto medular, al cual deseamos aproximarnos: el sencillo cálculo de una suma de dos números naturales. Sabemos que, si preguntamos a un computador por la suma de dos números enteros positivos, sin importar cuáles sean, la máquina procederá al cálculo de la adición que se le solicita. Igualmente, si se tratara de una multiplicación de los números entregados. De hecho, nos parece que al aparato le da igual sumar que multiplicar. Esto es lo que nos impactaba en los años setenta, cuando proliferaron las calculadoras.
En contraparte, sabemos que, para nosotros, las personas, la adición y la multiplicación nos representan dos problemas de distinta dificultad, léase: puedes sumar 37 + 42, de manera relativamente fácil, pero no así al intentar responder a la operación análoga de 37 x 42. Por otro lado, podríamos seleccionar dos números muy grandes, que el proceso computacional concluiría, para el tiempo humano, en lo que juzgaríamos como un instante. Aquí, amerita una acotación, para indicar que un calculador numérico se encuentra, por lo usual, restringido a operar con cierto número de cifras, digamos una o dos decenas, pero lo importante es comprender que una computadora se puede programar para recibir un número cualquiera de cifras.
Pues bien, vamos a ejemplificar con un caso pequeño, para comprender el proceso de recursión, y también, la potencia de la recursividad en computación. Piénsese en 5 + 8, que sabemos y estamos claros que da por resultado 13. Como es usual, solemos ver las cosas y nuestro entorno, inclusive el que nuestra mente plantea, en términos de nuestras perspectivas humanas. Creemos y juzgamos a los otros agentes actuantes, como los animales, por ejemplo, en función de nuestras propias conductas. Somos inherentemente antropocéntricos. Empero, el asunto medular, es comprender que existen agentes que actúan sobre su entorno de manera muy diferente a como lo hacemos los humanos. Esa es una primera conclusión: los autómatas operan diferente.
Lo decimos desde un inicio, pues conviene enfocarnos en esta distinción que estamos subrayando. El caso de 5 + 8 es tratado en nuestra mente de una forma que no se encuentra vinculada con el cómputo por parte de una máquina electrónica. Por ejemplo, no sería extraño suponer que un primer paso en nuestro proceso mental fuera el de transformar la pregunta, para partir del 8, que es el mayor de los dos números, y posteriormente agregarle 5. Esto implica que nuestro algoritmo mental tiene un primer paso, seleccionar el mayor de los dos números naturales a sumar. En este caso, los permuta.
Paso seguido, quizá por la técnica «de los dedos», y porque usamos el sistema de numeración decimal (porque tenemos diez dedos), es posible que a este 8 de partida le calculemos el complemento aritmético, que es lo que falta a 8 para completar el orden decimal, en este caso, las decenas. Como a 8 le faltan 2, para llegar a 10, de 5 sustraemos 2, para saber cuánto sobra, obteniendo 3. Así concluiremos que la suma solicitada es una decena y tres unidades, o sea, 13. Aunque no lo hayamos reflexionado previamente, resultará interesante que el lector y lectora reparen en este procedimiento.
No obstante, la interrogante principal es cómo realiza una máquina una operación como esta, enfocándonos en el papel que juega la recurrencia o recursividad. Al transparentar, a grandes rasgos, el funcionamiento de un autómata o computador, nos permitimos una mejor noción de lo que una máquina podría realizar. Esta arma secreta, subyacente en todo algoritmo, hace de la autorreferencia la base de una economía computacional. Los dos casos elegidos, nos ayudarán a la comprensión, aunque muchos otros pudieran funcionar de manera análoga. Al meditarlo un poco, podremos caer en la cuenta de que la recurrencia no es algo tan extraño, ni a nuestro pensamiento, ni a la forma en que la naturaleza se organiza, en medio de su complejidad sistémica.
Continuamos así, primero, con el caso de la adición de dos números naturales. Hemos tomado el ejemplar de 5 + 8. Explicamos que nuestra mente realiza la siguiente secuencia: 5 + 8 = 8 + 5 = 8 + (2 + 3) = (8 + 2) + 3 = 10 + 3 = 13. En la secuencia no se observa que el 5 fue descompuesto como suma de 2 + 3, porque 2 es el complemento aritmético de 8, esto es, lo que le falta a 8 para completar la decena, es decir, para llegar a 10.
Insistimos en el proceso mental humano que usualmente realizamos para obtener una suma, para caer en la cuenta de que el mismo es algorítmico. Al mismo tiempo, reparar en que tal proceso mecánico no tiene nada que ver con la forma en que el autómata procederá, como pasaremos a ver en lo que sigue. Lo primero será preguntarnos qué son realmente los números naturales para un computador, o, mejor dicho, cómo puede generarlos y manipularlos. Sabemos que un ordenador electrónico representa los números naturales en sistema binario de numeración, es decir, como secuencias de unos y ceros. En el artículo «Determinismo y computación», explicamos cómo el computador, mediante la función sucesor, puede calcular la secuencia de números naturales.
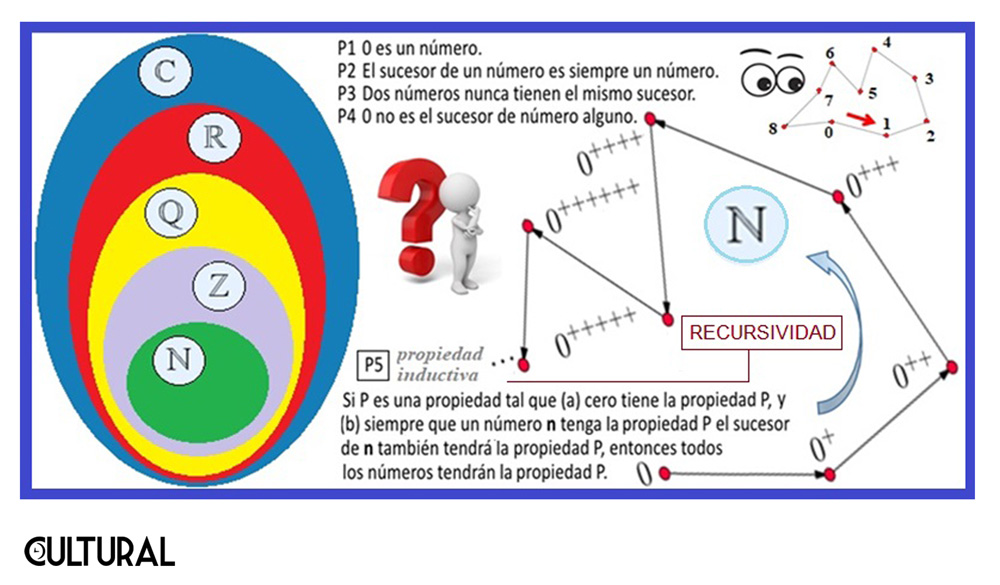
Esta función se califica de primitiva, puesto que, de ella y otras similares, se originarán todos los cómputos posteriores. Se encuentra incorporada físicamente en todo ordenador, y permite escribir el número siguiente a una secuencia de entrada dada. Dado una cadena de ingreso, que represente el número natural N, el autómata podrá escribir, esto es, calcular, la cadena para el sucesor de N, el número que le sigue, simbolizando la cadena de salida como N+.
Así, existe una función primitiva sucesor, tal que a cada número natural N le hace corresponder el número siguiente, así: sucesor :: N à N+. Es claro que el valor de N+ es N + 1. Por ejemplo, sucesor (19) = 20, o bien 19+ = 20. En binario, las cadenas correspondientes irían así: sucesor (10011) = 10100. Con ello se establece que el sucesor de 19 = 100112 es 20 = 101002. En teoría de computación, son tres los procesos primitivos, a saber: a) la función cero, que escribe 0 en el dispositivo (coloca una cadena que contiene solo ceros); b) la función sucesor, que acabamos de describir; y c) la recurrencia primitiva, sobre la que estamos escribiendo.
Pues bien, el cómputo de una suma se hace mediante una recursión. Se requerirá escribir en un lenguaje de computador, el equivalente a la definición recursiva que aparece en la siguiente imagen, en la parte superior izquierda. En breve, la definición establece que: a + n+ := (a + n)+. El símbolo := es equivalente a otro, también muy utilizado, =def. Ambos símbolos se leen como «definido por», siendo usados para establecer que el término que aparece en la izquierda del símbolo se está definiendo por la expresión que aparece en la derecha. Trátese de descubrir cómo opera este concepto, estudiando, a continuación, un ejemplo de su aplicación.

En la imagen previa también se muestran otras tres definiciones recursivas, a saber: para la multiplicación, la exponenciación y el cálculo de los coeficientes binomiales. Como dijimos, la recursividad de un concepto «recurre», o sea, regresa, a sí mismo. Si se observa, en la definición a + n+ = (a + n)+, se dice que, para ejecutar una adición, que se está definiendo, hay que realizar otra adición. Esto parece redundante o circular, una broma de mal gusto, porque si no sé operar con +, no suena razonable que me envíen a realizar tal operación. Es como que me digan: «mira, para sumar, tienes que sumar». Por ello el epígrafe, que parece gracia, pero no lo es, como pasamos a ver.
Cuando uno lee la expresión definitoria, a + n+ := (a + n)+, uno lee la igualdad y muy posiblemente no termina de descubrir lo que se dice, mucho menos lo potente de un concepto así. Sí se pone un poco de más atención, veremos que nos dice que para sumar n+, debo, primero, sumar n, y luego calcular el operador sucesor. Hay una diferencia substancial, porque en la izquierda está la adición de n+, mientras en la derecha está n. ¿Qué significa? Pues, que estoy trasladándome de una suma dada a otra más simple, porque n es más pequeño que n+. Y esto suena razonable, o más familiar, porque un problema dado lo estoy transformando en otro más sencillo.
Si regresamos a la imagen previa, veremos que el proceso de sumar 3, se transforma en el proceso de sumar 2, y luego en el de sumar 1, hasta que llegamos al proceso de sumar 0, que es el caso de base, el que sí se sabe ejecutar. A final de cuentas, la máquina calculará a+++, que equivale a a + 3, como se ilustra en la imagen. De esta forma, cuando a la máquina se le pida calcular 8 + 5, terminará transformándolo, por recursividad, a 8+++++, es decir, calculará la quinta iteración de sucesor sobre el número 8. La pregunta original, de 5 + 8, la hemos cambiado, únicamente, por motivos de facilidad en la lectura.
Recapitulando, al definir una operación recursivamente, es fundamental cumplir con dos condiciones o requisitos: a) que lo que se define pueda ser representado por funciones ya ejecutables en la máquina, pudiendo incluir la función que se define; y b) que se establezca un caso base o primitivo. En el caso de la adición, se utiliza como función ejecutable la primitiva sucesor, y se anota como caso base el hecho que a + 0 = a. Obsérvese que las tres definiciones recursivas mostradas arriba, utilizan operaciones previamente ejecutables, y colocan, para cada situación, el caso base a utilizar. Véase, por ejemplo, que la definición de la multiplicación, (n+1) a := a + na, recurre a la adición, ya definida y ejecutable, y al caso base: 0a = 0.
En adenda, la imagen siguiente, muestra cuatro casos más de definiciones computacionales recursivas. Para el número uno, el caso del factorial de un número entero, y el número tres, de la secuencia de Fibonacci, se ilustran corridas de ejemplo del cálculo: a) para el factorial de 3, 3! = 6; b) para el cuarto elemento de la sucesión, f4 = 3. Conviene comentar que el algoritmo que sigue la definición recursiva de la sucesión de Fibonacci es tremendamente ineficiente, porque genera un árbol de llamadas demasiado extenso, que crece exponencialmente, pudiendo llegar a dejar «trabada la máquina». Así, no porque un algoritmo sea ejecutable (proceso computable), significa que sea bueno (eficiente). Esto, claro, será material para otra ocasión.

El segundo caso lo paso a describir muy rápidamente. Se trata de una de las variedades de los algoritmos del tipo «divide y vencerás». Imagínate que quieres ordenar un centenar de documentos, numerados del 1 al 100. Una técnica que intuitivamente se sigue, es partir el bloque inicial en dos partes. Si cada uno de los bloques parece muy extenso, se sigue subdividiendo, hasta llegar a un tamaño que uno pueda ordenar eficientemente sobre una mesa, cercano a una docena documentos. Se ordena cada grupito, del menor al mayor, y se procede luego a la inversa, integrando de dos en dos los grupos ya ordenados.
Alguien podría pensar: ¿en dónde se encuentra aquí la recurrencia? La idea sigue siendo la misma, porque el algoritmo ordenar incluye un subalgoritmo partir, e, internamente, una nueva llamada a ordenar. Nuevamente, la iteración del algoritmo de la llamada a sí mismo se detiene cuando se llega al tamaño idóneo para el algoritmo de base, en el que sí es posible ordenar el grupo más pequeño, que para los humanos anda alrededor de la decena de casos. La misma lógica podrá realizar el computador, que se puede ver beneficiado con esta técnica de división, sea por la capacidad de los subalgoritmos o sea por la eficiencia conjunta obtenida. Conviene citar, en este momento, al mismo Alan Mathison Turing:
La idea detrás de las computadoras digitales puede explicarse diciendo que se trata de máquinas cuyo objetivo es ejecutar cualquier operación que pueda realizar una computadora humana. Esta computadora humana supuestamente sigue reglas fijas y carece de la autoridad para desviarse de ellas en el más mínimo detalle.
Por otro lado, sobre la broma del inicio, dice la Wikipedia:
La recursividad se emplea a menudo de forma humorística en textos informáticos, filosóficos o matemáticos. No es raro que un libro de texto de estas disciplinas incluya en su glosario una entrada similar a esta: «Recursividad, véase Recursividad». Otro ejemplo es cuando, anteriormente, en Google, al buscar «recursión», el sitio apuntaba «Quizá quisiste decir: recursión».
Otro ejemplo de esta situación humorística se observa en lo frecuente que resulta la elección de acrónimos recursivos. Un prototipo de esto es PHP, que son las iniciales de «Preprocesador de Hipertexto PHP». Sin embargo, más allá de las bromas, quisiéramos continuar en un próximo artículo, con las reflexiones y comentarios ofrecidos. Aunque no queremos caer en el plano de los políticos de mala plana, el hecho es que se nos ha agotado el espacio de esta oportunidad. Para cerrar, respecto a la historia del pensamiento recursivo, el columnista Fernando Flores Morador, a menos de tres meses de su partida, escribía en su artículo «La inteligencia artificial», de su columna «Cambalacheando», lo siguiente:
Originalmente, la inteligencia artificial se redujo a estructuras de feedback. Por ejemplo, Ctesibio de Alejandría (250 a. C.) construyó la primera máquina retroalimentadora, un regulador del flujo de agua. En su libro Ars magna, de 1315, Ramón Llull concibió la idea de que el razonamiento podía ser reproducido independientemente de la mente humana. Pero es a partir del siglo XX que el razonamiento artificial basado en entreactos graficados, alcanza la complejidad y la efectividad suficiente para el [ denominado ] razonamiento artificial
Fuente de imágenes ::
[ 1 ] Imagen tomada de gAZeta, editada por vbc :: https://www.gazeta.gt/la-cuarta-revolucion-industrial/
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/Recursi%C3%B3n + https://es.wikipedia.org/wiki/Recursi%C3%B3n_(ciencias_de_computaci%C3%B3n) + https://es.wikipedia.org/wiki/Definici%C3%B3n_recursiva
[ 3 ] Imagen tomada de gAZeta, editada por vbc :: https://www.gazeta.gt/determinismo-y-computacion-ii/
[ 4 + 5 ] Imágenes elaboradas por Vinicio Barrientos Carles







