Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
El área exacta es la raíz cuadrada del producto de la mitad de la suma de los lados disminuida por cada lado del cuadrilátero.
Brahmagupta
La palabra geometría proviene del griego γεωμετρία, término que a su vez los filósofos y matemáticos antiguos construyeron como integrado por el prefijo γῆ (gē), tierra, vinculado a su vez con la deidad primordial Gea, y el sufijo μετρία (metría), que significa medida. Ante esta descomposición etimológica, resulta clarísima la acepción original del término, como el estudio de los sistemas para la medición de la tierra, es decir, para determinar el tamaño de las extensiones de las superficies, fueran estas para el cultivo, para el pastoreo o para cualquier otro posible uso.
Por ello, la geometría se refiere, desde un inicio, a un arte o técnica de naturaleza abstracta, porque no toma en cuenta los particulares usos o tipos de suelo, sino que trabajará con idealizaciones de estas superficies, no alejándose por ello de su aplicación práctica, que vendría a ser la resolución de un problema concreto tomado de la realidad fáctica, esa que está atada a los hechos del mundo tangible.
Sin embargo, en la mente contemporánea, esta significación dista mucho de lo que uno una joven entiende en la actualidad por geometría. El escolar promedio vincula esta palabra con una materia en los programas formativos, provenientes y heredados del trivium y el quadrivium medieval. De esta forma, el o la estudiante identificará más la geometría con la palabra «teorema», con las denominadas demostraciones y con las fórmulas, como en es el caso del volumen de una esfera, cuyo volumen es, cabalmente, dos tercios del volumen del cilindro que la circunscribe, según estableció Arquímedes de Siracusa.
En efecto, la Geometría, como disciplina formal, es una rama de la Matemática que se ocupa del estudio de las propiedades de los objetos definibles en un determinado espacio, siendo estas propiedades basadas en los conceptos provenientes del sistema de la geometría plana del clasicismo griego, en donde se incluyen objetos como puntos, rectas y planos, y relaciones entre los objetos, como congruencia, paralelismo, perpendicularidad, coplanaridad y otras, llegando a generalizaciones tales como curvas y superficies. Esta concepción deriva de uno de los textos más reproducidos y divulgados a lo largo de la civilización humana: los Elementos de Euclides.
No obstante, a pesar de esta concepción clásica, hemos escrito en este Suplemento Cultural LaHora sobre los objetos en espacios multidimensionales, de los cuales los polígonos y los poliedros estándar son casos particulares en dos y tres dimensiones euclídeas, respectivamente. Empero de esta extensión al espacio tridimensional, o estereometría, un estudio riguroso de las relaciones geométricas siempre tendrá su fundamento y su punto de partida en el caso basal de la geometría plana, es decir, la del espacio euclidiano bidimensional.
Hoy deseamos presentar con quien nos lee, a un eximio matemático y astrónomo indio, Brahmagupta, quien vivió en el siglo VII, en la ciudad de en Ujjain, en donde fue el director del más famoso y antiguo observatorio de astronomía. Considerado el más grande de los matemáticos de esos siglos, es bastante desconocido en Occidente. Para aproximarnos a uno de sus más notables aportes, empezaremos con uno de los primeros problemas planteados en la geometría plana, este que dio origen al término mismo, como hemos comentado: el cálculo de la extensión de una determinada superficie en el plano.
El caso más sencillo proviene del cálculo del área de un triángulo, que consiste en el conteo de unidades básicas de área incluidas en el triángulo en cuestión. El área básica viene dada por un cuadrado de medida unitaria. Este problema de la determinación de cuántas unidades de área contiene una cierta superficie, hace de la práctica geométrica uno de los procesos científicos más antiguos, aunque inicialmente estos constituyeran un cuerpo de reglas pragmáticas respecto al uso y aplicación relativo a las longitudes, las áreas y los volúmenes. Aunque alguien quizá recuerde el adagio «la mitad del producto de la base por la altura», en la imagen siguiente se muestra una demostración visual para el cálculo del área de un triángulo cualquiera.
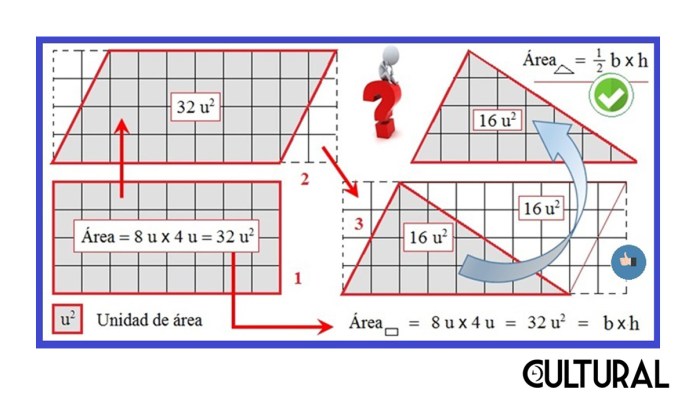
Desde las civilizaciones más antiguas, léase sumerios, acadios y babilonios tempranos, la incorporación de algoritmos, o procesos abstractos sistemáticos en la medición geométrica, representan los primeros indicios de la aplicación de la inteligencia humana, en problemas más complejos, yendo más allá de la inmediata seguridad biofísica y de la supervivencia. Ejemplo de ello son los anales que versan sobre la invención de la rueda, abriendo posteriores problemáticas, tales como el descubrimiento y la definición del número π.
También amerita resaltar los antecedentes del antiguo Egipto, como un preámbulo a la sistematización que los matemáticos griegos harían de la Geometría, elevándola a la construcción axiomática y deductiva por excelencia, aspectos claves en el desarrollo intelectual del pensamiento occidental. La mayoría de conceptos que aprendemos en la escuela estaban ya contemplados en la geometría griega, pero, en particular, un extenso estudio sobre los triángulos, que vienen a ser como las piezas fundamentales de la geometría plana. También aprendemos algunos términos referentes a los distintos tipos de cuadriláteros y su efectiva identificación. Se muestran algunos en la izquierda de la imagen siguiente.
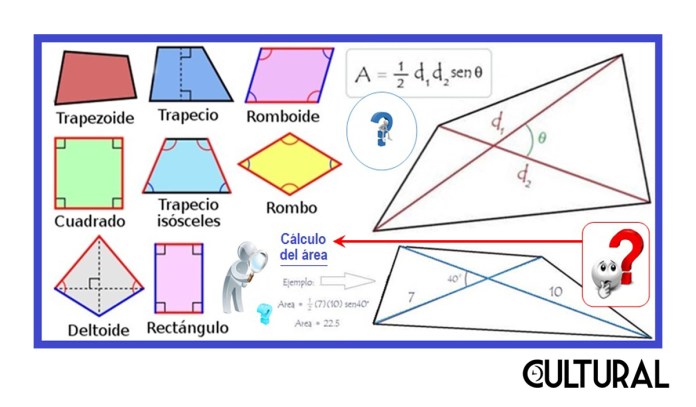
Si se observa, se muestra una fórmula para el cálculo del área de un cuadrilátero cualquiera, no necesariamente un paralelogramo. Como apreciamos, no nos resulta familiar: el área se calcula como la mitad del producto de las dos diagonales del cuadrilátero por el valor de la función seno del ángulo entre las dos diagonales. Como veremos, Brahmagupta desarrollo una fórmula epónima para el área de un cuadrilátero, conocidos sus cuatro lados.
Sin embargo, la fórmula más sencilla para el área de un cuadrilátero es esta que se ha mostrado, pues requiere únicamente de tres datos: el valor de las dos diagonales y el valor del ángulo entre ellas. Se ha incluido un ejemplo de su aplicación, para el caso de un cuadrilátero cuyas diagonales miden 7 y 10 unidades respectivamente, siendo el ángulo de 40°. Al aplicar el algoritmo, obtenemos un área estimada de 22.5 unidades cuadradas, o unidades de área (22.5 u2).
Como curiosidad, obsérvese que, si conocemos el valor de las dos diagonales y el ángulo entre ellas, el cuadrilátero no está totalmente determinado, pues hay muchos cuadriláteros con diagonales de valores 7 y 10, que tienen un ángulo de 40° entre ellas, como puede el lector apreciar si juega con dos lápices de esos valores en centímetros, esto es, de 10 cm y 7 cm respectivamente. Desplace los lápices entre sí, pero conservando el mismo ángulo entre ellos. Aunque son cuadriláteros diferentes los que resultan, se tiene que el área de cualquiera de estos será exactamente la misma, esto es, aproximadamente 22.5 cm2.
Como se pudo apreciar en la primera imagen, el concepto de área está basado en unidades cuadradas, básicamente porque la cuadrícula, un mosaico basado en cuadrados, posee muchas ventajas conceptuales y operativas, que inclusive son fácilmente extensibles a cualquier número de dimensiones, aunque en la Antigüedad se consideraran únicamente los casos de los espacios de dos y tres dimensiones, por el estado de madurez de las matemáticas de aquellos entonces, las cuales estaban indefectiblemente vinculadas con los fenómenos concretos, esos que podríamos llamar del «mundo real».
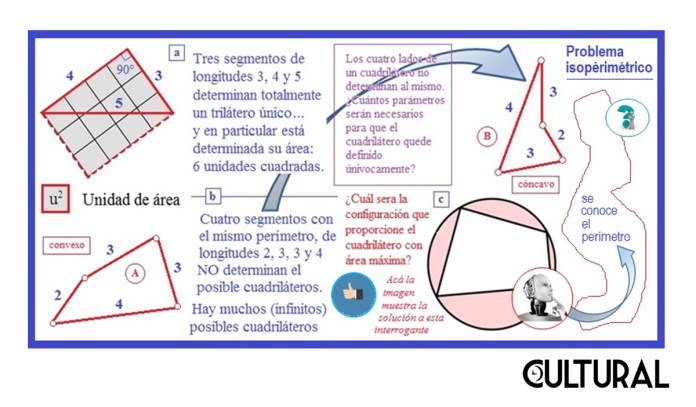
En este contexto hizo su aparición un problema abstracto originario, denominado el problema isoperimétrico, que consiste en relacionar la longitud y naturaleza de una periferia con el área de la región que delimita. En la imagen siguiente se presenta el caso general, sin restricción respecto a la barda que define la frontera de la región, y otro, en la izquierda, con la restricción de que la periferia está conformada por cuatro segmentos de longitud fija, de manera que se busca un cuadrilátero que posea cierta área, y en particular un área maximal. El matemático Brahmagupta resolvió el asunto de encontrar el área máxima que puede obtenerse al dar los valores de los cuatro lados de un cierto cuadrilátero, mediante los denominados cuadriláteros cíclicos.
En complemento, cabe comentar algo al respecto del desarrollo y la diversificación de la Geometría a lo largo de la historia. Notables los aportes de grandes intelectos, como los de Leonhard Euler y Carl Friedrich Gauss, ya en el ámbito de la Modernidad, quienes condujeron a sentar las bases para el posterior desarrollo de la Topología, una creciente rama de la Matemática, así como, aunado a los aportes de Bernhard Riemann, de la Geometría diferencial, una de las tantas subdisciplinas de la Geometría actual.
Estos procesos hacia la abstracción llegaron a un punto crítico con el programa de David Hilbert, referido a su propuesta de construir un sistema axiomático formal que sea completo, y que abarque a toda la matemática conocida, o al menos a las disciplinas matemáticas elementales. Cuando se axiomatiza algo, en un sistema puramente deductivo, los objetos se convierten en entes abstractos, ideales, ausentes de todo significado concreto, teniendo que la aplicación de sus relaciones y derivaciones formales (teoremas) en determinados aspectos de la realidad fenoménica (sensible o concreta) vienen a constituirse en los modelos matemáticos de esos aspectos de la realidad.
En lo anterior. resulta crucial comprender el fracaso de tal proyecto formalista de Hilbert, a raíz del teorema de incompletitud de Kurt Gödel, que redunda directamente en el alcance y los límites de todo sistema científico, basado, en última instancia, en modelos y teorías formales. Podremos extendernos posteriormente sobre estos aspectos, pero, por ahora, regresemos al problema del área de un cuadrilátero cualquiera, el cual Brahmagupta resolvió de manera sobresaliente.
Hemos comentado sobre el problema del isoperímetro, con restricción poligonal. Nótese que tres segmentos determinan, en forma unívoca, un polígono de tres lados. Dados tres segmentos, se determina un único un triángulo. Sin embargo, cuatro segmentos no lo hacen, puesto que existen muchas figuras poligonales de cuatro lados, cuadriláteros, con áreas diferentes, que pueden ser construidos con los cuatro segmentos dados. Convendrá pensar en un ejemplo concreto.
Supóngase que se tiene una cerca con longitud 12 m. Si este perímetro se divide en tres segmentos específicos, se obtendrá un único triángulo, con un área determinada o definida. Por ejemplo, si los segmentos miden 3 m, 4 m y 5 m, tendremos el familiar triángulo de área 6 unidades cuadradas, dado que la base mide 4 m y la altura 3 m. Sin embargo, si esta misma periferia, de 12 m, se partiera en cuatro segmentos, se notará que no queda determinado un único cuadrilátero. Cabe preguntarse cuál será el cuadrilátero que encierre un área máxima, o mínima, teniendo definidos los cuatro segmentos, digamos de tamaño 2 m, 3 m, 3 m, y 4m, que suman 12 m. ¿Cuál será la relación que debe tenerse para lograr este efecto óptimo, de máximo o mínimo?
Curiosamente, la intuición nos dice que, si queremos un área chica, habrá que «estirar» los segmentos, para hacer un «cuadrilátero delgado», mientras que para hacerlo maximal, el de mayor extensión posible, habrá que «redondearlo» lo más posible, para hacer un «cuadrilátero gordo». Nuestra intuición no está errada, y aunque en la historia del pensamiento matemático se llevó algún tiempo para establecer formalmente este tipo de aseveraciones, las mismas no dejan de ser interesantes.
En ejemplo previo, suponemos los segmentos que conforman el cuadrilátero como fijos, y la interrogante es ¿cómo colocarlos para maximizar (o minimizar) el área que estos cuatro segmentos encierran? Vemos cómo, de preguntas iniciales muy prácticas, referidas a la medición de un terreno, se puede pasar a cuestionamientos mucho más abstractos, y este fue justamente el proceso evolutivo que la Geometría llevó a cabo, siendo el caso general para toda la Matemática.
En breve, partiendo de la definición del área de un rectángulo, que es muy transparente, dado que la cuadrícula misma determina su área, la interrogante matemática será cómo podremos calcular el área de un cuadrilátero cualquiera, por ejemplo, ese que hemos dibujado en la imagen previa, cuyos lados miden 2, 3, 3, y 4 unidades de longitud. En particular, hemos preguntado ¿cuál será la configuración que proporciona el cuadrado maximal, asumiendo que se conocen las longitudes de sus lados?
La respuesta viene dada por el concepto de cuadrilátero cíclico, o inscrito, que es aquel que resulta perfectamente inscrito en una circunferencia, o equivalentemente, que existe una circunferencia que lo circunscribe, de manera tal que sus cuatro vértices pertenecen a esta circunferencia. Obsérvese que, todo triángulo posee una circunferencia que lo circunscribe, pero no así todo cuadrilátero. Por lo general, al encontrar una circunferencia que pase por tres vértices cualesquiera, resultará que el cuarto no estará sobre esa circunferencia. Cuando si se puede circunscribir una circunferencia en un cuadrilátero, este se llamará cíclico.
El caso más general del problema del isoperímetro es tomar una cuerda de una longitud dada y ver cómo debe disponerse para encerrar con ella la mayor extensión de área posible, y de qué tamaño sería esta área. La naturaleza y nuestra intuición, íntimamente relacionada con nuestras experiencias sensibles, nos dirán que la cuerda, o perímetro dado, deberá colocarse en forma circular. Esto, a pesar de ser fácilmente comprensible, no es necesariamente fácil de probar, y sobre esto ameritará que regresemos en forma más detallada. El análogo tridimensional se sucede cuando tenemos una extensión de superficie dada y deseamos encerrar con ella el mayor volumen posible. Bastará inflar un globo de goma para ver que la solución vuelve a ser el objeto tridimensional «más redondo» posible: la esfera.
Regresando a la escuela primaria, recordaremos que estudiamos el triángulo, o trilátero, como la figura plana más sencilla posible. No obstante, la noción de extensión de una superficie plana, o área, se origina en otra figura plana, el cuadrilátero, que como bien indica su nombre, consta de cuatro lados (que son segmentos de recta), en lugar de tres, como sucede en el caso del triángulo. Nótese el detalle en el uso de los términos, pues todo triángulo es trilátero, y viceversa, mientras que los conceptos de cuadrilátero y cuadrángulo no son necesariamente correspondientes. Para caer en la cuenta, inténtese construir, o imaginar, una figura que tenga cuatro segmentos de recta, pero que no tenga exactamente cuatro ángulos.
Pues bien, hemos visto que una superficie, en su sentido usual, está conformada por dos dimensiones, es decir, tiene un ancho y tiene un largo, por lo que su medición deberá contener estas dos medidas. El principio métrico del desplazamiento paralelo establece, para el caso bidimensional, que el volumen, tamaño, viene dado por el producto de la medida del segmento que se desplaza por la medida del desplazamiento, esto es, la multiplicación del largo por el ancho. Si se piensa en un rectángulo, se verá que la medida de su tamaño, de su área, es proporcional a cada lado.
Esto implica que el área de un rectángulo, o de un paralelogramo, en general, que tiene el mismo ancho, tendrá un valor que será directamente proporcional a su largo, o bien de forma conversa, si el largo es fijo, el tamaño del área será proporcional a la longitud de su ancho. De esto que el área viene dada por el producto de dos valores, independientes entre sí… su ancho y su alto. Esto puede generalizarse fácilmente, al tamaño, o volumen, de un cuerpo n-dimensional, que involucraría un producto de n factores, generando una medida con unidad métrica n-dimensional. El caso prototipo son las hipercajas, constituidas por un cierto número de hipercubos unitarios n-dimensionales, aunque hemos hablado de las hiperesferas y de otros sólidos comunes en los espacios euclídeos de mayor cantidad de dimensiones.
La intención de hacer justa memoria a Brahmagupta, proviene del hecho que, en su obra maestra, el Brāhmasphuṭasiddhānta, este incluye una fórmula mediante la cual se calcula el área de un cuadrilátero cíclico, conocidos los valores de sus cuatro lados, según describen los versos del epígrafe. Tal método de cálculo se conoce como la fórmula de Brahmagupta, la cual se aprecia, en el lenguaje y simbolismo matemático contemporáneo en la imagen siguiente.
Esta fórmula, que data desde el año 620, aproximadamente, hace ver que, conocidas las longitudes de los cuatro lados de un cuadrilátero, el área será máxima cuando el cuadrilátero sea cíclico, es decir, cuando pueda inscribirse perfectamente en un círculo, lo que sucederá, cuando y solo cuando, sus diagonales sean perpendiculares entre sí, hecho a su vez conocido como el teorema de Brahmagupta. Abajo, en la imagen, puede verse que, si las diagonales son ortogonales, se tendrá que θ = 90° = π/2, y por lo tanto cos θ = cos (π/2) = cos 90° = 0, de donde el radicando obtendrá un valor máximo en ese caso, porque el último término, que es negativo, se hará cero.
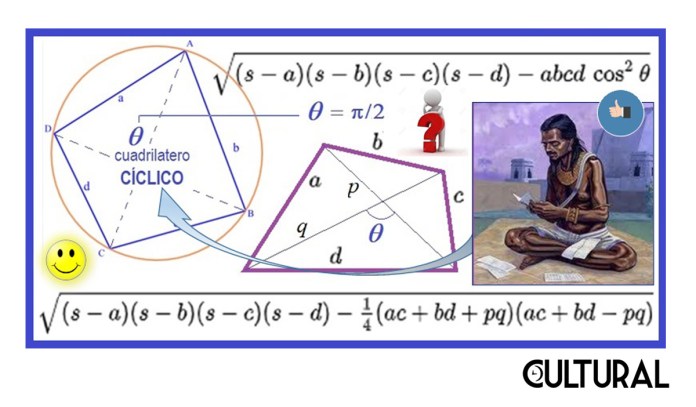
Esta particularidad del área máxima es general, para cualquier polígono de n lados, el cual adquirirá su óptimo cuando el polígono pueda inscribirse en una circunferencia, asumiendo como fijos los valores de los lados de este n-polígono. Por otro lado, nótese que, si en la fórmula de Brahmagupta se tuviera que uno de los lados toma el valor cero, es decir, si se hace que uno de los lados se haga tan pequeño hasta anularse, se obtendrá la más conocida fórmula de Herón de Alejandría (ca. 50 d. C.), la cual calcula el área de un triángulo en función del valor de los tres lados. Así, podemos concebir un triángulo como un cuadrilátero que tiene uno de sus cuatro lados con valor cero.
En complemento, obsérvese que todo triángulo es cíclico, porque siempre es posible circunscribir una circunferencia en el triángulo dado. Sobre Herón hemos escrito en el artículo «El circulo del triángulo y las tres partes de Herón». Hasta aquí nos quedamos en lo referente a la fórmula de Brahmagupta, con la motivación para dar oportuna continuidad a los temas.
No obstante, unas reflexiones finales en torno de la geometría. Iniciamos apuntando que γεωμετρία significa, en el griego original, medición de la tierra. Aunque se origina como una sistematización de reglas prácticas, los antiguos, y especialmente la racionalidad griega, la van elevando hasta los altares de un modelo de acercamiento a la verdad por excelencia, desde el momento en que configuran el sistema deductivo formal como el único que resulta independiente de las percepciones sensibles, las que proceden de los sentidos fisiológicos, siendo en contraposición un producto puramente intelectual.
La escuela pitagórica y su poderosa influencia en Platón generarán esta concepción, a tal punto que el sabio filósofo coloca en el frontispicio de la Academia de Atenas la siguiente inscripción: «no pase acá quien no sepa Geometría». Sin embargo, este cambio de lo pragmático a lo puramente abstracto no fue ni inmediato ni fortuito, como estamos tratando de esbozar. Un largo y complejo proceso se llevó a cabo. De hecho, tiene mucho que ver con la imperante idea de la necesidad lógica que subyace en ciertos hechos, que no son contingentes, sino necesarios, aquellos que tienen de darse a fortiori.
En este sentido, el desarrollo del pensamiento matemático está indefectiblemente ligado a esta fuerza racional, a la contundente realidad lógica de que hay ciertas situaciones que quedan totalmente determinadas cuando se dan otras. La idea de la implicación es fundamental en el edificio matemático, y la noción de teorema es el ladrillo fundamental en tal construcción. Si ciertas premisas se presentan, entonces, con imperativa fuerza, deberán darse otras. Esto maravilló a los antiguos, y la Geometría es justamente el modelo perfecto de esta necesidad lógica de fuerza.
En cierta forma, liberarse de la contingencia y la casualidad resolvía la problemática del caos originario del cosmos. En cierta medida, la Matemática y los objetos de los que se ocupa, gozaban de la eternidad y ni siquiera los dioses del Olimpo escapaban de la finitud como lo hacen los objetos formales de tipo matemático. De ahí la teoría de las ideas en Platón: inmutables, perennes, libres de corrupción, eternas. De alguna manera, la mayoría de matemáticos contemporáneos son en cierta medida platónicos formalistas. En vista de nuestras cortas fuentes sobre Brahmagupta, no podremos saber lo que este magnífico matemático indio pensaba al respecto.
Fuente de imágenes:
[ 1 … 4 ] Imágenes elaboradas por Vinicio Barrientos Carles, editadas y tomadas de gazeta :: https://www.gazeta.gt/la-formula-de-brahmagupta/ + https://www.gazeta.gt/el-area-de-un-cuadrilatero-i/ + https://www.gazeta.gt/el-area-de-un-cuadrilatero-ii/








