Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Este es un universo matemático. Estamos rodeados de ecuaciones y sumas.
Steve Maraboli
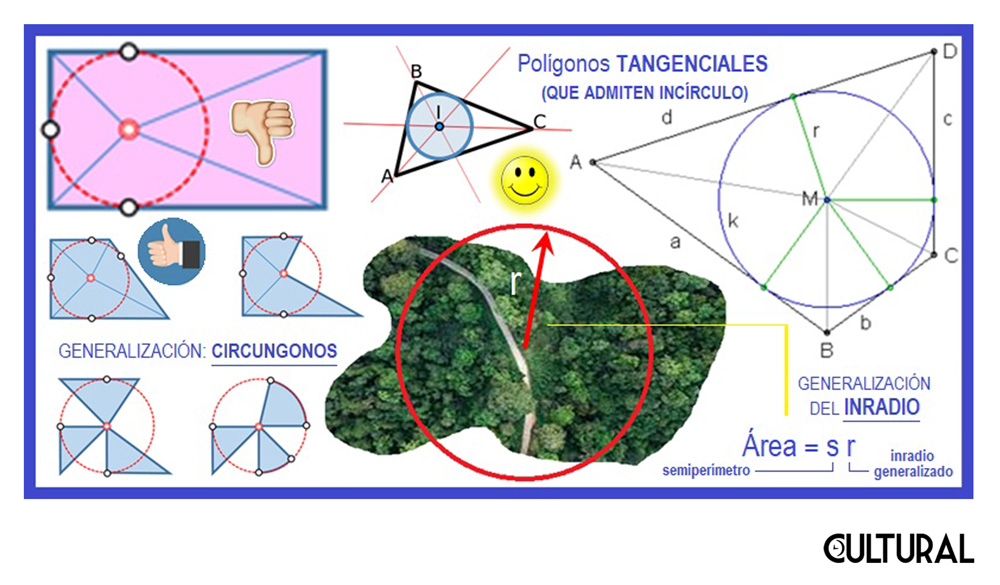
En la pasada publicación introducimos la noción del incírculo, o circulo circunscrito. Establecimos que algunos polígonos poseen un incírculo, único y bien definido, como el caso del cuadrado, mientras que otros no, como en el caso de un rectángulo que tenga sus lados de distinto tamaño. De hecho, se mencionó que los polígonos que aceptan un circulo inscrito único se llaman polígonos tangenciales, justamente porque existe una circunferencia que queda inscrita en el polígono y resulta tangente a cada uno de sus lados, esto es, que los toca en únicamente un punto, el punto de tangencia.
En la situación planteada de los polígonos tangenciales, decimos que el incírculo está inscrito en el polígono, o bien, de forma recíproca, que el polígono está circunscrito en el círculo. Es decir, el círculo inscribe al polígono, o bien, el polígono circunscribe al círculo. Por ello mencionamos que a los cuadriláteros tangenciales se les llama también cuadriláteros circunscritos, en donde se sobreentiende que lo que se circunscribe es un cierto círculo. Al respecto apuntamos:
para que un cuadrilátero sea circunscrito (esto es, tangencial) se requiere que tenga dos pares de lados opuestos que sumen igual. Esta caracterización es de doble vía. Si tiene un par de lados opuestos que sumen igual, entonces es tangencial y posee incírculo. Si posee incírculo, entonces tendrá dos pares de lados opuestos que suman igual.
Estas caracterizaciones, o equivalencias no evidentes de conceptos, son las que mayor utilidad presentan, tanto en el desarrollo teórico del edificio matemático, como en lo que respecta a las aplicaciones prácticas. Por ejemplo, si tenemos un terreno poligonal de cuatro lados, de forma que un par de lados contiguos suman 20 m, mientras el otro par suma igual, sabremos que existe un círculo que queda perfectamente inscrito en el terreno, tangente a cada uno de sus lados. El radio de este incírculo será el inradio del terreno. Vimos, a su vez, que el área de este polígono tangencial, cuadrilátero en este caso, sería igual al producto del semiperímetro por el inradio: Área = ½ p r = s r.
En medio de la presentación de estos conceptos insistíamos que la Matemática (o las matemáticas, como algunos autores prefieren denominarlas) se refiere a cierto tipo de sistemas formales, y su objetivo es encontrar este tipo de relaciones que emergen del sistema como verdades de razón, es decir, que se deben cumplir con fuerza lógica. Empero, que comprendemos esta finalidad y sus posibles aplicaciones, lo verdaderamente asombroso en la Matemática es la insospechada interconexión que existe entre los sistemas mismos, interrelaciones que fortalecen y potencializan de manera sobresaliente las temáticas. De hecho, existe una belleza sin par en estos lazos, que invisibles, una vez desvelados, implican novedosas formas de trabajo e investigación.
Como bien dice el título de esta oportunidad, hoy vincularemos el incírculo de un triángulo con un problema numérico, del que posiblemente no tenemos idea que pudiera existir. Como podremos apreciar, después de la lectura de este breve artículo, algo increíble pasará a nuestro acervo matemático y cultural. Para empezar, nos concentraremos en el caso del incírculo de un triángulo plano, que, como comentábamos la vez anterior, siempre existe. Esto significa que todo triángulo, cualquiera que sea, es tangencial, a diferencia de los cuadriláteros, en los que algunos lo son y otros no, habiendo descrito cuando se da cada situación. Tan particular es el incírculo del triángulo, que cuando se busca «círculo inscrito» suele aparecer el caso triangular.
Como hemos apuntado, una de las características más hermosas, y más sorprendentes también, es la interconexión entre una subárea matemática y otra. Vayamos, pues, al grano. Creo que todos y todas conocemos dos situaciones que nos parecen especiales y familiares a la vez. La primera, aquel triángulo rectángulo, que tiene lados de valores enteros, a saber: 3, 4 y 5. Podemos apreciarlo en la ilustración que sigue, la imagen N° 2. La segunda refiere a la secuencia 1, 2 y 3, la que casualmente hemos sumado, obteniendo 6. Lo curioso es que si en vez de sumar, multiplicamos, obtenemos el mismo 6, puesto que 1 x 2 x 3, el denominado factorial de 3, que solemos simbolizar mediante 3!, es también 6.
Así, al observar que 1 x 2 x 3 = 1 + 2 + 3 = 6, puede resultar razonable preguntarse si existirán otros tres números que cumplan con esta propiedad: que al sumarlos se obtenga el mismo valor que al multiplicarlos. A diferencia de la situación de una pareja de números, este problema no es fácil, algebraicamente hablando, porque al tratarse de tres números cualesquiera, cualquier abordaje con variables nos solicitará alguna información extra. No obstante, quien nos lee se preguntará: ¿qué relación tienen las dos particularidades expuestas: el triángulo y la terna de números? ¿Y qué tiene que ver ese Herón mencionado en el titular? Veamos con detenimiento la imagen siguiente.
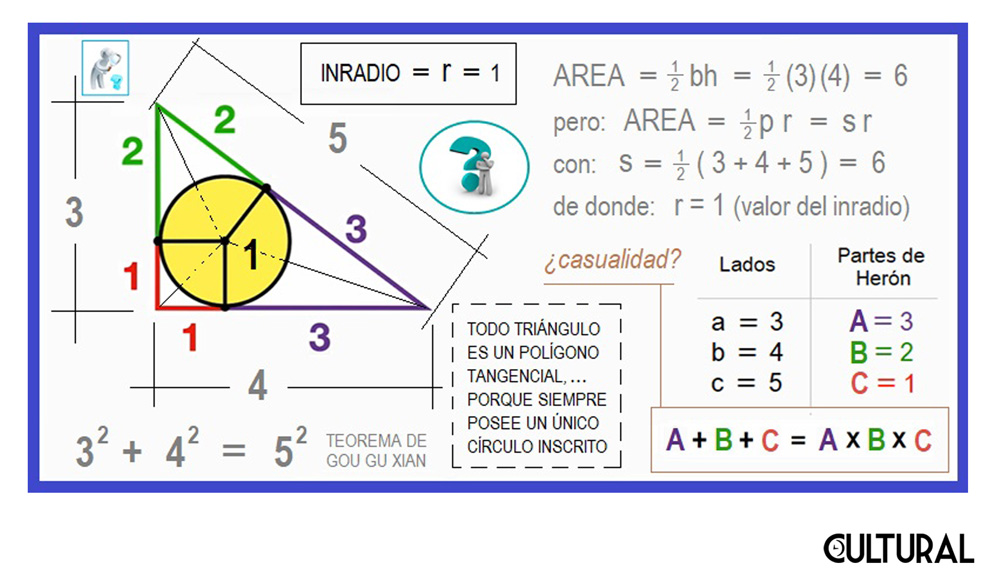
Apreciamos el incírculo del triángulo 3 – 4 – 5, observando los puntos de tangencia del mismo, así como las medidas de las partes que quedan definidas en cada uno de los lados. Para no creernos todo lo que nos dicen, es importante notar que el área del triángulo es 6, porque sus lados, que son perpendiculares, miden 3 y 4 respectivamente. Para que se cumpla lo que hemos mencionado, de que el área es el semiperímetro por el inradio, tenemos que el inradio, el radio del círculo inscrito debe ser 1. En la imagen, a su vez, hemos querido representar gráficamente la validez de la fórmula: que el área debe ser la mitad del perímetro por el inradio.
Pues bien, la vinculación, que ahora parece una simple casualidad, es si los valores de los segmentos 1 | 2 | 3 tienen algo que ver con lo que hemos citado, que 1 + 2 + 3 = 1 x 2 x 3. ¿Tiene algo que ver o es una simple contingencia? ¿Existe alguna relación? Esta es la parte de las conjeturas, la más excitante de todas, en donde surge una pregunta y una posible respuesta que haga ver que un hecho no es una casualidad, sino una generalidad, que siempre tendrá que darse. Una conjetura matemática pasa por todo un tamiz de procesos, bajo la inquietud de alguna posible nueva verdad matemática: un nuevo teorema.
Es el momento conveniente para traer a colación al eximio ingeniero y matemático de la Antigüedad, de quien cabe hacer una cita sobre su papel en la historia de la ciencia:
ejerció de ingeniero en su ciudad natal, Alejandría [, considerándosele] el mayor experimentador e inventor de la Antigüedad y su trabajo es representativo de la tradición científica desarrollada durante la época helenística [, recordado…] principalmente por la Fórmula de Herón, una forma de calcular el área de un triángulo usando únicamente las longitudes de sus lados.
Este posible conocimiento de la fórmula que se menciona, ilustra de manera ejemplar lo que el pensador Paulo Freire solía calificar de una educación bancaria, basada en el aforismo de «calla, trágatelo y no preguntes». Aunque nos son nuevas las críticas que realizamos al sistema educativo escolar formal, nunca está de más insistir, tratando de hacer reflexión y consciencia al respecto de los males. Como hemos dicho, lo valioso de los procesos mentales matemáticos radican en la demostración, la racionalidad de que ciertas cosas deben ser forzosamente de cierta manera, como cuando razonamos que el área de un triángulo dado es la mitad del producto de un lado cualquiera por su altura correspondiente.
Sin embargo, a Herón se atribuye un procedimiento que recurre a los valores de los tres lados. Después de todo, si nos vamos a la práctica, al colocar tres pilotes en un terreno, habremos definido un triángulo, único, y por lo tanto con un área perfectamente definida. Aunque la idea de utilizar la altura es sencilla, teóricamente, en la práctica es distinto, pues lo que puedo obtener, con relativa facilidad, son las longitudes de los lados de la cerca, es decir, el valor de cada uno de los tres lados del triángulo. A Herón se debe la fórmula que determina el área en ese caso, que viene a ser el más natural y útil de todos.
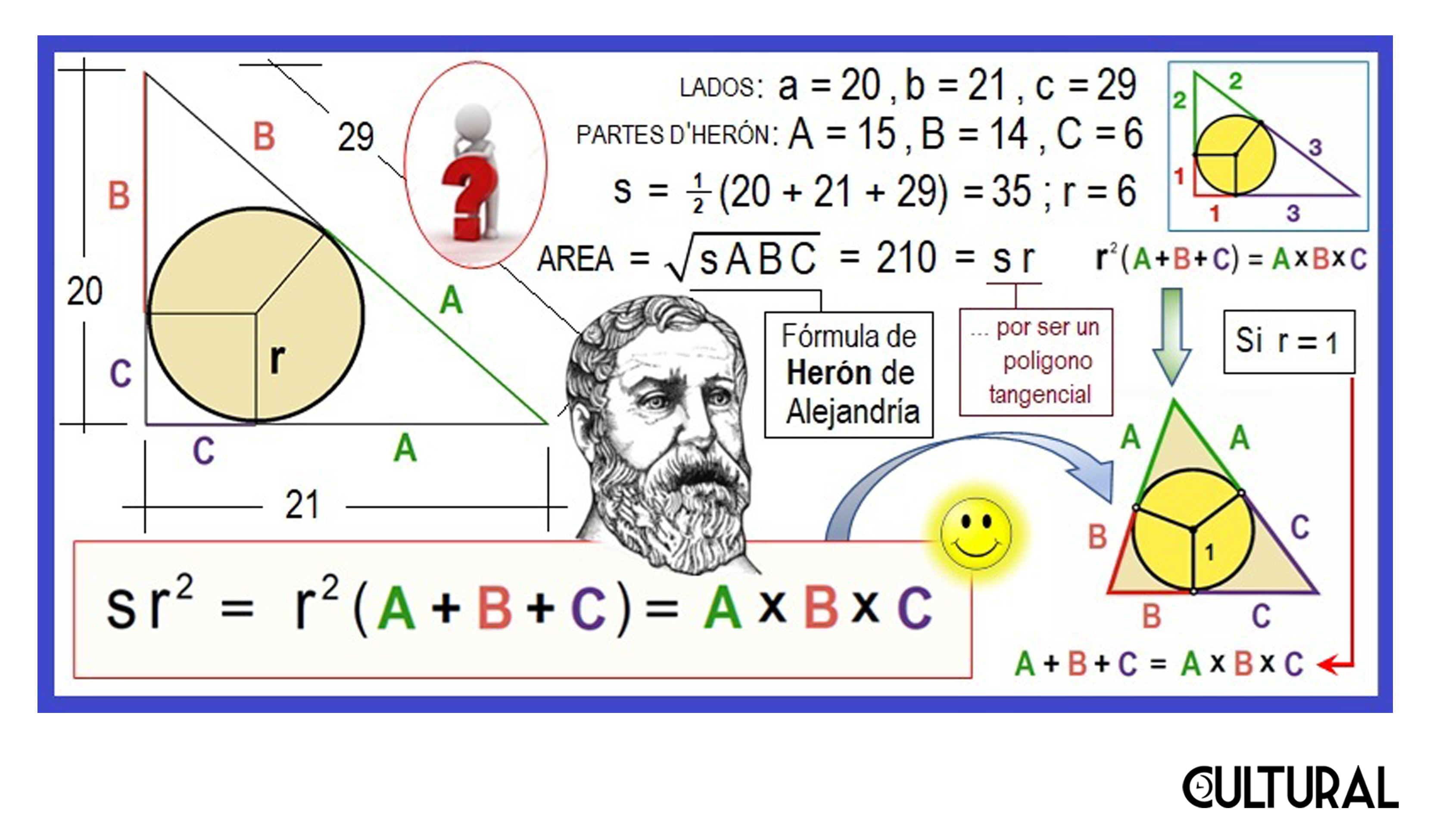
Si los lados de un triángulo valen 20, 21 y 29, la fórmula de Herón calcula que el área será de 210, sin conocer ninguna de las alturas del triángulo. No obstante, la importancia de la Matemática no es realizar cálculos como este, pues para eso están las máquinas, que operan algorítmicamente. La verdadera importancia de la Matemática descansa en su poder racional, en la demostración de los teoremas, lo cual, en gran medida, no es un asunto de cálculos ni de algoritmos. De ahí nuestras críticas, pues muy difícilmente alguno conoce una prueba de la fórmula del alejandrino, Herón, y aunque el lector, o lectora, no lo crea, el incírculo es parte clave en el asunto.
Pero regresando al tema, podríamos aventurarnos a conjeturar que los tres segmentos que define el incírculo cumplen con la propiedad que mencionamos: que su producto es igual a su suma. Y nuevamente, aunque el lector o lectora no lo crea, de manera fabulosa, esto es precisamente lo que sucede, con una pequeña condición. Las ventajas de esta interconexión temática son sublimes. Qué es más fácil: ¿pensar en tres números que sumen igual que su producto? ¿O dibujar un triángulo cualquiera y pasar a medir esos segmentos que define el incírculo? En definitiva, la segunda opción se presenta como más amigable.
Con regla y compás, de manera empírica, o usando trigonometría, podríamos encontrar otros tres números que cumplieran la propiedad deseada, esto es, que A + B + C = ABC. No haremos una demostración rigurosa, pues no es nuestro objetivo, pero en la imagen N° 3, la última, se aprecia un triángulo cualquiera, en el que se ha trazado su círculo inscrito. Allí se observan los tres segmentos que quedan determinados por los puntos de tangencia. De parte nuestra, les hemos denominado a estos tres segmentos las «partes de Herón», y las estamos simbolizando por A, B y C, según se opongan a cada uno de los lados del triángulo dado, a, b y c, respectivamente
Existe un detalle importantísimo, y es que para que A + B + C = ABC, el inradio debe valer 1, lo que puede hacerse mediante proporcionalidad, o asumiendo el valor de la unidad como el valor del inradio. Es decir, si quien nos lee desea obtener tres números A, B y C que cumplan la propiedad buscada, que su producto sea igual a su suma, lo único que tiene que hacer es tomar regla y compás y proceder a un cierto procedimiento. Primero traza tres líneas no paralelas, de manera que al cruzarse determinen los vértices de un triángulo. Después, traza el círculo inscrito, para finalmente medir las partes de Herón que quedan definidas… y voilá.
En lo anterior se asume que ese trazo del incírculo es algo bien sabido, puesto que «al ojo» va a ser un poco difícil el trazado exacto. Lo que se requiere es el trazo de las tres bisectrices, pues donde se intersecan estas tres rectas será el incentro, o centro del círculo inscrito buscado. Es un trazo no muy complicado que puede resultar entretenido. Aunque pudieran ser divertidos los aprendizajes de posibles procedimientos, no es ciertamente lo esencial.
Hoy en día existen herramientas de software que hacen todo este tipo de cosas, e, insistimos, que lo medular y relevante son los conceptos. En unos años, apenas, nos encontraremos diciéndole a una máquina: «dibújame el incírculo», y el autómata obedecerá de manera impecable al pedido. Le podríamos dar, en alternativa, el valor de las longitudes de los tres lados (a, b y c) y el aparato nos escribiría, ante nuestra solicitud, el valor de las tres partes de Herón (A, B y C). Con el tema de que el radio inscrito, o inradio, deba tener el valor de 1, lo que se hace es un escalamiento, que significa agrandar o achiquitar cada valor longitudinal en el mismo factor.
En la imagen última hemos colocado el ejemplo previamente citado, de un triángulo de lados 20 – 21 – 29, que como en el caso inicial del famoso 3 – 4 – 5, se trata de un triángulo rectángulo. Esto lo hemos hecho así por facilidad, y para que los lados tengan valores enteros. Las ternas previas, ambas, son llamadas ternas pitagóricas, pues son valores naturales que corresponden a los lados de triángulos rectángulos. En otra ocasión veremos cómo pueden encontrarse triángulos así. Por ahora, verifíquese que el lado mayor es una hipotenusa, esto es, se trata de triángulos con un ángulo recto, pues cumple con el famoso teorema de gou gu xian: c2 = a2 + b2.
El tiro es que, en el triángulo 20 – 21 – 29, el círculo inscrito tiene un radio de valor 6. Si disminuimos los valores de cada lado en este factor, el valor del inradio, obtendremos tres partes de Herón que cumplen con la condición solicitada: que su producto tiene igual valor que su suma, como en el caso inicial, bastante fácil, de que 1 + 2 + 3 = 1 x 2 x 3. Si recordamos, 1, 2 y 3 son las partes de Herón del triángulo de lados 3 – 4 – 5, que tiene un inradio de valor 1, como es requerido. Para el caso del triángulo 20 – 21 – 29, el inradio vale 6, y las tres partes de Herón valen 6, 14 y 15.
Para tener los tres números del triángulo 20 – 21 – 29, disminuimos cada lado en un factor de 6, de manera que las tres partes de Herón del triángulo original, que son 6 – 14 – 15, ya disminuidas, pasarán a ser 6/6 = 1, 14/6 = 7/3 = 2+1/3 ≃ 2.33333, y finalmente, 15/6 = 5/2 = 2½ = 2.5. Hemos obtenido entonces tres nuevos números que cumplen con que su suma sea igual que su producto. Simbolizando 7/3 ≃ 2.33333 como 2.3+, los tres números en cuestión están en { 1 , 2.3+, 2.5 }. Verificando, tenemos que, en efecto: 1 + (2.3+) + 2.5 = (1) (2.3+) (2.5) = 5.83+ = 35/6.
Cerrando, cabe recalcar, que lo trascendental, lo verdaderamente importante, no son los cálculos, o las posibles «soluciones» al acertijo numérico que hemos planteado, sino la asombrosa relación que existe entre una rama de la disciplina y la otra, entre unos objetos geométricos, los triángulos y sus incírculos, y un problema muy singular en otro campo, el aritmético. Estas equivalencias, o isomorfismos (aunque el término está prestado y no es técnicamente preciso), vienen a exponer bellezas que permanecen escondidas a los ojos del lego, al común de todos los mortales.
Únicamente los matematikoi de la antigua escuela del gran Pitágoras pueden llevarnos a ellas, elevándonos por encima de nuestra finitud, que como bien expresaba Platón, es tan solo sombra de las ideas perfectas que habitan fuera de este mundo sensible. O, como también lo manifestaba Carl Friedrich Gauss, el llamado príncipe de la Matemática: «Los encantos de esta ciencia sublime, sólo se les revelan a aquellos que tienen el valor de profundizar en ella». Y aquí nos quedamos, en la expectativa que todo esto resulte motivante, de una u otra manera, sea en el mundo de las formas, sea en el mundo de la cantidad, sea en cualquiera de los otros mundos que coexisten, a veces sin percatarnos de ello.
Fuente de imágenes ::
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: https://lahora.gt/lh-suplementos-culturales/la-hora/2022/11/12/el-incirculo-y-una-interesante-propiedad/
[ 2 + 3 ] Imágenes elaboradas por Vinicio Barrientos Carles








