Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Lo que los hombres realmente quieren no es el conocimiento, sino la certidumbre.
Bertrand Russell
En el anterior artículo, en este Suplemento Cultural LaHora, titulado «Datos, conocimiento y predictibilidad», hacíamos ver que, en vista de nuestros deficientes sistemas educativos, solemos tener una idea errónea al respecto de muchas temáticas y áreas del conocimiento. La estadística es indefectiblemente una de estas áreas. De hecho, la palabra «estadística» la relacionamos con datos, gráficas y porcentajes, pero usualmente nos quedamos ahí, lo cual es un signo de este desconocimiento que menciono. Es decir, esta asociación con gráficos y tablas de datos es insuficiente, pues oculta el sentido científico que posee y su aplicación en nuestra vida del día a día.
Cabalmente, en el citado artículo, explicaba esto de la forma científica de procesar lo que se nos muestra: el fenómeno. En el paradigma estadístico bayesiano, el utilizado por las máquinas que aprenden, es fundamental la distinción entre «lo que son las cosas» y «lo que aparentan ser». Algo de esto mencionamos en el artículo «Deep machine learning: conceptos y reflexiones». También mencionamos que este ha sido un tema de reflexión filosófica, que se origina en la Antigüedad, íntimamente relacionado con el concepto del cambio, puesto que las apariencias cambian, pero las esencias permanecen. De esta y otras maneras más se plantea históricamente la oposición entre el fenómeno y el noúmeno.
Por otro lado, sobre la actitud dogmática, contraria al saber científico, hemos escrito:
Únicamente en el pensamiento ingenuo podríamos aceptar que las cosas son como las percibimos, es decir, como «se nos muestran». [En contraposición,] en ciencia, en filosofía y en cualquier ejercicio racional riguroso, debemos aceptar y comprender plenamente que la manifestación de las cosas, o de los hechos, no siempre coincide con esas cosas, o esos hechos, de manera tal que no estamos plenamente en la «verdad» cuando creemos que poseemos la certeza de ese algo que aseveramos.
Esto significa que, aun en el caso más simple, de una consideración binaria, dicotómica, al respecto de una determinada situación, existe un cuadro conceptual fundamental que explica cómo podemos estar errados en nuestras consideraciones epistemológicas. Se trata de una tabla 2 x 2 que muestra la relación entre el fenómeno que se manifiesta y la realidad, desconocida, al menos parcialmente. Regresemos al par de ejemplos, icónicos, por cierto, que hemos comentado en el artículo precedente, para ejemplificar esta dicotomía y por qué hablamos de una tabla 2 x 2. Son los casos de la enfermedad y de un cierto proceso judicial, un juicio.
Con la primera situación, sabemos y aceptamos que nos podemos enfermar. Es decir, aunque usualmente estamos sanos, también, de vez en cuando, perdemos el equilibrio en nuestra salud, y caemos enfermos, como solemos decir. Ciertos signos nos indican este desequilibrio. Les llamamos síntomas, porque lo sentimos. Otros signos no son perceptibles, por nuestros sentidos, pero sí se ven reflejados en una prueba de laboratorio bioquímica. Aquí vemos la distinción entre dos aspectos. Por un lado, la enfermedad, que puede ser planteada en forma binaria: la tenemos o no la tenemos. Por el otro, el signo, la apariencia, que también se puede dicotomizar: se muestra o no se muestra.
Dado que tenemos dos dicotomías, hablamos de un esquema 2 x 2, que, en efecto, produce cuatro casos: enfermo con signos, enfermo sin signos, no enfermo con signos y, finalmente, no enfermo sin signos. Esto es profundo, porque está relacionado con la lógica de la causalidad, por un lado, pero con el saber empírico científico que utilizamos con gran frecuencia, sin darnos cuenta. En la causalidad pura, o consecuencia lógica, tenemos que A ⇒ B, lo que significa que siempre que se da A, entonces, necesariamente, tendremos B. Sin embargo, al observar B, no podemos saber si A se ha presentado.
Ilustremos la idea. Si se tuviera que una enfermedad dada produce fiebre, que es un síntoma, o signo, al observar la fiebre, no podríamos concluir que tiene la enfermedad. Por ello podemos tener el caso de un no enfermo con signos, porque sabemos que todo enfermo presentará los signos, pero también existen otras situaciones que producen esas mismas condiciones. En otras palabras, podemos tener que A ⇒ B, pero también C ⇒ B. Al observar B, no sabemos si su causal es A o es B. Esta situación es una parte esencial de la noción de implicación lógica.
Por el otro lado, tenemos el sentido empírico de la ciencia, pues muchas veces no es posible establecer causalidades puras, en un sentido lógico estricto, sino únicamente correlaciones muy elevadas. Es decir, podemos observar que el 99 % de los pacientes de cierta enfermedad presentan un determinado signo. Así, la opción de enfermo sin signo es factible. Aunque no sea lo usual, es posible que alguien padezca la enfermedad y no posea el signo. En la reciente situación del Covid, nos familiarizamos con los llamados asintomáticos. Aunque no se han enfermado, son portadores del virus, y la relación entre realidad y apariencia va por el mismo rumbo.
En la teoría de la decisión se trata con asuntos de este tipo, de una manera muy general. Cuando el médico ve al paciente, ve un cuadro de síntomas, pero debe emitir un diagnóstico, debe decidir si lo que observa es real, o es aparente. Me recuerdo de una osa, en un cierto zoológico, que presentó todos los síntomas de embarazo, por lo que los encargados procedieron a proporcionarle la comida extra y las vitaminas del caso. Al pasar de los meses, pudieron percatarse que se trataba de un embarazo «fingido», por el interés del úrsido en los beneficios y el buen trato. Aunque los signos, las apariencias, indicaban el especial estado de gravidez, la realidad era otra.
En términos generales, ante un determinado fenómeno, tenemos estos mismos cuatro casos posibles, pues podemos afirmar lo que observamos, como real, o podemos negarlos. Así, las cuatro opciones se reparten en dos, cuando afirmamos o negamos, estando en lo correcto (en la «verdad»), y otras dos, cuando afirmamos o negamos, equivocándonos en cada caso. Estadísticamente siempre existe una probabilidad de que te equivoques, sea que afirmes, sea que niegues. Cuando al afirmar erramos, incurrimos en un error de tipo I, error α (alfa), mientras que cuando erramos al negar, incurrimos en un error de tipo II, error β (beta).
Aunque las matrices de detección/decisión tienen abundantes usos en campos especializados como los diagnósticos de cualquier clase, el control de la calidad, las telecomunicaciones y la psicología de la percepción, son aplicables en todo cuanto procesamos en nuestras mentes. La relación que estas matrices guardan con la Estadística científica o Matemática proviene de la subárea de la estimación estadística, en la cual se persigue estimar una variable aleatoria desconocida, denominada el estimando, a partir de su relación con otra variable aleatoria mejor conocida, denominada el estimador.
Acá, este mejor «conocimiento» se traduce en hechos, un tanto, más objetivos, como que el estimador es observable, y mejor controlable, que el estimando. Es frecuente ubicar el estimador en las filas y el estimando en las columnas. En el caso del enfermo, el estimador son los signos o síntomas, mientras que el estimando es la enfermedad. Así, en general, el estimador P (Prueba) corresponde al diagnóstico, indicador o evidencia, según sea el enfoque, mientras que el estimando R (Realidad) es aquello que se desea conocer, parcialmente desconocido. Lo que decido, pienso o expreso, está en el nivel P, mientras que la «cosa verdadera» está en el nivel R.
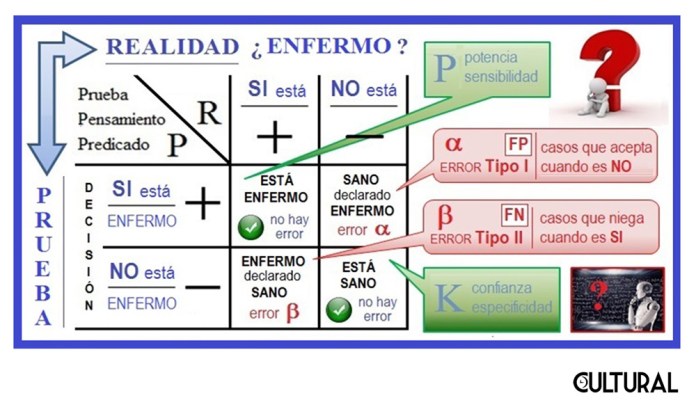
Pues bien, estos conceptos son ampliamente utilizados en el enfoque bayesiano de la probabilidad, en el que las probabilidades representan grados de creencia, usualmente subjetivos. Este enfoque ha tenido un repunte relevante en diversas aplicaciones de las ciencias sociales y, como hemos mencionado, en el desarrollo y auge de las herramientas de la inteligencia artificial. En el artículo «La estadística bayesiana y el aprendizaje automatizado» colocamos un ejemplo de aplicación de los conceptos. Se tenía a 300 personas clasificadas de acuerdo a dos criterios, su sexo y su condición de fumador. Se construía así una tabla de contingencia de 2 x 2, con los cuatro casos posibles, de acuerdo a los dos criterios binarios.
Nótese que, en este ejemplo, el sexo es observable directamente, mientras que la condición de ser fumador no lo es. Por ello, el sexo pasa a ser un indicador de la realidad de ser fumador o no serlo, es decir, el sexo es el signo o prueba (P), el estimador, mientras que la condición de ser fumador será la realidad desconocida (R), el estimando. De aquí que la observación del sexo viene a ser una evidencia, o prueba diagnóstica, para estimar la probabilidad de que una persona sea fumadora o no.
El asunto medular del proceso bayesiano es que la probabilidad de estimación de R, la condición de ser fumador, mejora, se hace más precisa, con el conocimiento del estimador P, del sexo. En el caso mostrado en la anterior oportunidad, se tiene una probabilidad de ser fumador, llamada probabilidad a priori, porque no vincula en nada con el hecho de ser mujer u hombre. Mediante un algoritmo bastante simple, llamado la regla de Bayes, se pasa a calcular las probabilidades condicionales, o marginales, que constituyen las probabilidades a posteriori, la mejora en el modelo. La probabilidad de ser fumador, sabiendo si es hombre o mujer, mejora la estimación inicial.
Estas probabilidades condicionales operan con un conocimiento extra, que produce, al tratarse de una población más específica, una probabilidad más cercana a la distribución real. Cada dato extra que se incorpora al modelo va generando probabilidades más precisas, de manera que las predicciones son paulatinamente mejores.
En el ejemplo presentado, usando dos cifras significativas, se tenía que la probabilidad simple (a priori) de ser fumador era P(F) = 57 % (170 de 300). No obstante, con el conocimiento adicional del estimador, el sexo, se tenía que la probabilidad condicional de ser fumador si se es hombre era P(F|H) = 67 % (120 de 180), mientras que la probabilidad de ser fumador si se es mujer era P(F|M) = 42 % (50 de 120) si es el caso de una mujer. Si una máquina observa que ingresa una persona al almacén, asumirá un 57 % de probabilidad de que quiera comprar cigarrillos, pero si reconoce que es mujer, la probabilidad bajará al 42 %.
Imagine el lector si esta máquina, artificialmente «inteligente», agrega una considerable cantidad de variables más en sus observaciones… en cuánto mejorarán sus estimaciones sobre la estimación de la compra que desea realizar. Después de cincuenta datos en calidad de estimadores P, por citar un número, la probabilidad de la conducta esperada será tan precisa que la máquina se dirigirá a esta persona como el vendedor ideal, casi «adivinando» por qué está ingresando al susodicho almacén. Así de potente es este esquema, recursivo y paulatinamente mejorable.
Con esto, hemos ilustrado la aplicación de la inferencia estadística, en la que resulta fundamental el reconocimiento y la distinción de los elementos que hemos colocado en el titular. En paralelo, estamos concibiendo la Estadística como una ciencia en íntima conexión con las inferencias que hacemos, con base en datos de tipo empírico, aportando un grado de certeza y de error en las aseveraciones que realizamos. Basándonos en los hechos disponibles, estas inferencias siempre se realizarán en un marco general de incertidumbre y desconocimiento. Por esta razón encontraremos los métodos estadísticos presentes en las distintas investigaciones científicas, o en aquellas publicaciones que revistan cierta seriedad académica.
Por otro lado, es importante reconocer que siempre tenemos un acercamiento parcial a las cosas, porque de alguna forma siempre estamos observando tan solo una porción de los fenómenos. Muy difícilmente podemos tener un contacto con «la totalidad» de las cosas. Es decir, nuestro contacto con la realidad siempre es parcial, mediante muestras, sin abarcar el todo. Esta parcialidad en nuestras observaciones nos lleva a una certidumbre siempre limitada, con cotas, lo que significa que aquello que consideramos verdadero, cierto, puede contener algún pequeño componente de error o sesgo.
No considerar esta posibilidad, denominada error estadístico, sería tremendamente ingenuo y equívoco por parte de un pensador riguroso, totalmente responsable de lo que afirma o de lo que cree. Este error estadístico es muy distinto a una equivocación humana, lo que en el idioma inglés es bastante más claro al diferenciar entre los términos bias, error y mistake, equivocación. El sesgo es la siempre presente posibilidad, factual y formal, de que nos estamos desviando, levemente, quizá infinitesimalmente, del punto exacto en donde están realmente las cosas.
Cuando analizamos el caso del enfermo es crucial tener en mente este concepto del sesgo. Sin embargo, la situación se da en otro cualquier caso. Así como la enfermedad posee aspectos visibles, observables, los que hemos denominado signos de la enfermedad, también posee otros aspectos que no son del todo perceptibles desde el exterior. Similar sucede con el segundo caso, el de un proceso judicial. Debemos partir que una situación son los signos o evidencias, y otra es la realidad de las cosas.
En el caso del juicio, deberemos emitir un veredicto, tomar una decisión y expresar, con base en las evidencias, si el sujeto es culpable o inocente de lo que se le imputa. Sea una u otra la decisión, sea que afirmemos o neguemos, la estadística nos indica que siempre habrá un sesgo, un error presente, sea α o sea β, existe una probabilidad de error. De lo que se trata, es de minimizar ambas posibilidades. El otro asunto importante, es que, si nos concentramos en disminuir uno de los tipos de error, el otro, inevitablemente crecerá. Al reducir α, crecerá β, y viceversa. En suma, si se determina que alguien posee un atributo, siempre existe la posibilidad de un error, el cual desearemos sea lo más pequeño posible.
Uno podría preguntarse ¿qué será peor?: ¿liberar al culpable o castigar al inocente?, ¿declarar enfermo al que está sano o dictaminar como sano a quien se encuentra enfermo? En cualquiera de los casos, estaremos dirigiéndonos a la minimización de uno de estos dos tipos de error. Como se ha mencionado, el error α–ALFA implica la probabilidad (o frecuencia) de errar cuando aceptamos la prueba P como fuente de la verdad en R, y corresponde al interés prioritario de la investigación. Por ello se habla de la significancia de la prueba, relacionada con la confianza K, o especificidad, de la prueba (K = 1 – α). Una prueba con especificidad del 95 %, implica un error α = 5 %.
Respecto al enfoque sobre la orientación que debe darse a los signos o pruebas, conviene reflexionar que para el médico lo importante será detectar la enfermedad, mientras que para el fiscal será evidenciar la culpa del acusado. En ambos ejemplos se definen los elementos sobre los que se desea depositas la confianza K, o especificidad de la prueba a realizar, relacionadas con el error de tipo I, o error α–ALFA . De manera inversa, el error β–BETA es aquel en el que podríamos incurrir al no aceptar nuestra hipótesis de investigación, el cual se encontrará relacionado con la potencia P, o sensibilidad, de la prueba (P = 1 – β). Será de abordar un ejemplo, que dejaremos para posterior oportunidad.
Para ilustrar el uso de una tabla dicotómica 2×2, en donde se contrasta lo que pensamos, lo que percibimos (fenómeno) versus lo que verdaderamente es, la «realidad», imagine, quien nos lee, una muestra hipotética de 50 personas de las que se sospecha están contagiadas con una de las variantes del coronavirus, una «nueva», de rápida propagación. La siguiente imagen muestra una posible situación resultante al realizar una cierta prueba de diagnóstico para esta variante del virus.
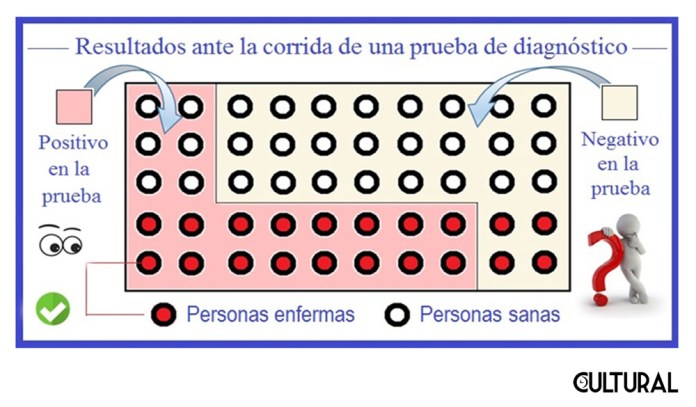
Insistimos en que se trata de una situación hipotética, pues se indica que los enfermos (infectados), son 20, y que los sanos (no contagiados) son 30. Empero, si supiéramos quienes están enfermos, no habría que realizar una prueba o test para identificarlos. Observe que resultan cuatro de forma natural: a) de los 30 sanos, hay 6 que salieron positivos y 24 que salieron negativos; b) de los 20 enfermos, hay 16 que salieron positivos y 4 que salieron negativos. O sea que el total se desglosa en cuatro grupos, incluidos en nuestra tabla dicotómica, de tamaño 2×2, así: 50 = 6 + 24 + 16 + 4. Esta separación obedece al cruce de dos aspectos: la realidad versus la apariencia.
Nótese que la tabla enfatiza esta separación entre lo que creemos que es, en base a los fenómenos observados, de lo que realmente es, oculto bajo las apariencias del mundo, por decirlo un tanto poéticamente. Así, una cosa es que alguien esté enfermo de esta nueva variante del Covid-19 (es decir, más correctamente, infectado con el virus SARS-CoV-2 de la variante en cuestión) y otra es que se piense que está enfermo (contagiado, para ser precisos). En la práctica de la clínica médica se observa que los síntomas (lo que se siente) y los signos (lo que se observa) pueden variar fuertemente de una persona enferma a otra, pero esto son otros detalles en lo que no ahondaremos.
El tiro es que no sabemos si alguien está efectivamente enfermo, y no lo podemos saber a simple vista, y esta ignorancia es la razón por la cual debemos realizar una prueba de diagnóstico. El análisis considera la interacción entre dos variables, una que es observable y otra que será una variable predicha o estimada en función de la anterior, que trabaja como estimador o predictor.
Previamente mencionamos el caso de una tabla de contingencia entre el sexo, que es observable, y el ser fumador, que no lo es, que será predicha por la primera. De igual o similar forma sucede con una enfermedad, pues lo que se observa, de lo que tenemos evidencia, es de los signos, mientras la enfermedad permanece oculta. Se trata de estimar la probabilidad de que alguien esté enfermo por medio de la observación de los signos. Esto es, se trata de estimar la realidad a partir de los fenómenos, de los datos que registramos en las apariencias.
Por ello el titular: datos, apariencia y realidad. En esta amalgama de conceptos es que entra en juego la prueba diagnóstica, que es la variable observable, o predictora, que hemos simbolizado por P, mientras la enfermedad es la variable a estimar, o predecir, simbolizada por R. La tabla en la imagen precedente los conceptos y el rol que juegan la confianza o especificidad (vinculadas al error α), y la potencia o sensibilidad (vinculadas al β). Es pertinente señalar que algunas variables predictoras serán «mejores» que otras, en el sentido de «equivocarse» menos.
En este sentido, existen dos formas en que una variable predictora, la prueba o test, se equivoque. Primero es cuando la prueba dice SI, pero realmente es NO; en este caso hablamos de un falso positivo (FP). En la imagen precedente, se ven casos en los cuales la prueba dice que SI está enfermo, cuando realmente está sano. En nuestro ejemplo numérico anterior, se trata de los 6 individuos sanos que dieron positivo a la prueba. La cantidad de falsos positivos, FP, se ve reflejada, cabalmente por el valor del error α. Aquí falló la confianza o especificidad de la prueba.
El otro tipo de error es cuando se diagnostica negativo a alguien que efectivamente está enfermo, o sea que la prueba dice NO, cuando se trata, en realidad, de un SI. En el ejemplo, estaríamos hablando de los 4 enfermos que dieron negativo, pero que efectivamente estaban enfermos. Insistimos que, como se aprecia en la imagen precedente, los falsos positivos (FP) están asociados a un sesgo, denominado error α–ALFA, mientras que los falsos negativos (FN) corresponderán al otro tipo de sesgo estadístico, denominado error β–BETA. En el último caso ha fallado la potencia o sensibilidad de la prueba.
Lo interesante es que se puede estudiar, previamente, estos parámetros analíticos de una prueba diagnóstico, o en cualquier tipo de predictor P. Si conocemos la sensibilidad de la prueba, conoceremos también error β en que se incurre. Si conocemos la especificidad, sabremos a su vez el valor del error α. Como mencionamos, numéricamente se complementan, en el sentido que cuando uno desciende, el otro aumenta. La idea será mantener un sano equilibrio.
Si la sensibilidad de una prueba es de 99 % entonces β = 1 %. Si la especificidad de la prueba es de 90 % entonces tendremos un valor de α = 10 %. Al regresar al asunto, obsérvese que la sensibilidad nos informa en el caso de que la prueba resulte negativa, pues una alta sensibilidad (potencia > 95 %) descartará la enfermedad en caso de una prueba negativa (porque β es pequeño). En sentido converso, una alta especificidad (confianza > 95 %) confirmará o indicará la presencia de la enfermedad en caso de prueba positiva (porque α es pequeño).
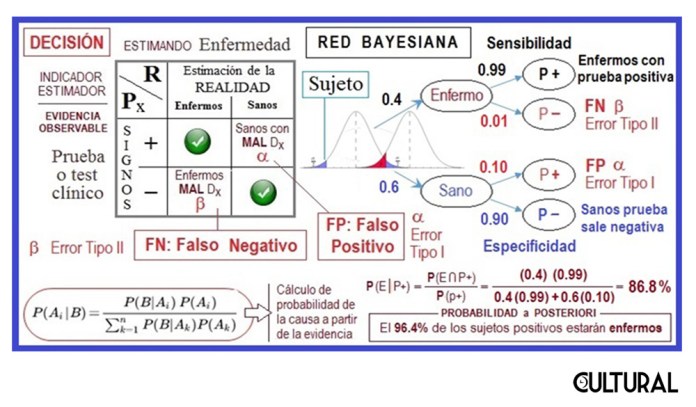
En la imagen previa se ilustra el uso de una red bayesiana para el cálculo de la probabilidad a posteriori para la condición de estar enfermo cuando la prueba sale positiva. Se usó una sensibilidad de 99 % y una especificidad de 90 %, correspondientes a las pruebas de RT–PCR (prueba molecular), obteniendo 87 %. Si se repite el cálculo con la prueba de antígeno se obtendrá que la probabilidad de estar infectado de Covid-19 cuando la prueba sale positiva es de 69 %. Repárese en el incremento en la incertidumbre, dado que el binomio sensibilidad especificidad ha descendido a 85 % – 75 %.
Cierto es que podríamos incluir otros parámetros que es posible obtener del análisis de la tabla 2×2 que hemos presentado. Es el caso de los denominados valores predictivos y las razones de verosimilitud, los cuales proporcionan gran ayuda en el proceso de diagnóstico profesional. Sin embargo, me parece que un razonable primer paso será la plena comprensión de esta diferencia entre la sensibilidad y la especificidad de una prueba, valorando su enorme utilidad. En general, de la observancia de los signos o evidencias se tomará una decisión al respecto de la realidad no observable directamente, y es aquí donde radica la importancia de los conceptos. Para finalizar, una última imagen, como ejercicio, para la lectora y el lector más inquietos.
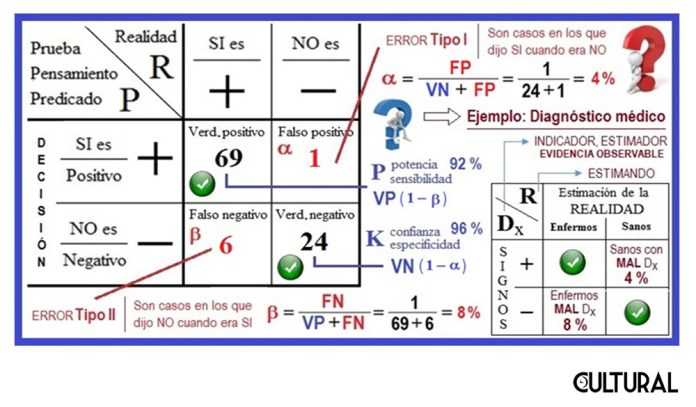
La idea subyacente es el conocimiento de una realidad, parcialmente desconocida, y de cómo se puede llegar indirectamente al objeto mediante los aspectos observables del mismo, esto es, de las evidencias o indicadores que de este podemos tener. Así, en suma, nuestras decisiones y nuestros conocimientos mismos dependerán de la estrecha relación entre las evidencias que poseemos y de la realidad que pretendemos conocer.
Como epílogo a la secuencia que hemos delineado, será conveniente estar claros de que, cuando tomamos una decisión, siempre existirá la posibilidad de inclinarnos por un «SÍ», cuando en realidad se trate de un NO. Estaremos entonces ante un falso positivo, lo que implica un error tipo I (error α). En la situación contraria, cuando nos decidamos por un «NO», tratándose en realidad de un SÍ, estaremos ante la probabilidad de un error de tipo II (error β), incurriendo en un falso negativo.
Fuente de imágenes ::
https://www.gazeta.gt/indicadores-estimadores-y-evidencias-i/ https://www.gazeta.gt/indicadores-estimadores-y-evidencias-ii/ https://www.gazeta.gt/sensibilidad-y-especificidad-en-una-prueba-de-diagnostico-i/ https://www.gazeta.gt/sensibilidad-y-especificidad-en-una-prueba-de-diagnostico-ii/








