Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Solo hay ciencia de lo que puede medirse. Florentino Ameghino
El conteo de cantidades discretas fue una de las primeras actividades matemáticas que el ser humano llevó a cabo. Era importante para las personas poder especificar, con precisión, cuántos elementos tenía una cierta colección, sea que se tratara de animales, productos, personas, en fin, se requería de un sistema de numeración que permitiera poder nombrar exactamente la cantidad de objetos de interés. El asignar identificadores para cada uno de los diferentes números naturales traía consigo innumerables ventajas. No obstante, dado que este conjunto de números naturales no tenía fin, era infinito, puesto que siempre se podía agregar una unidad al último natural considerado, se necesitada de un sistema, formal, que generara nuevos números naturales, sin límite alguno.
Este problema de construir un lenguaje que pudiera nombrar los números naturales, de simbolizarlos, tratándose en su totalidad de un conjunto infinito, implicó un proceso de abstracción de especial relevancia en el pensamiento humano. Posterior al conteo, se trataría de cuantificar las cantidades existentes en magnitudes continuas, aquellas que aceptaban subdivisión. Así, por ejemplo, las ovejas pueden contarse con los números naturales, porque dada una cantidad de ovejitas, tienes bien definida la cantidad siguiente. No puedes tener fracción de oveja, o tienes 2, o tienes 3, y así sucesivamente. Al considerar un posible fraccionamiento, aparece el proceso de medición. Aunque pudieras contar los frijolitos en un cierto recipiente, era más conveniente utilizar el mismo recipiente como unidad de medida.
Así fue como se pasó a considerar las unidades de medida para el caso de la cuantificación de magnitudes continuas, los patrones de medida. Aún hoy en día conservamos rescoldos históricos de antiguas unidades de medida, sea en los nombres (como el caso del pie), sea en las definiciones del patrón de medida, que usualmente estaban vinculadas con relaciones observadas en nuestro entorno (como el día, o la hora), o definidas por convención (como el metro: la diez millonésima parte del ecuador al polo norte terrestre). Sin embargo, actualmente, con los acelerados procesos de globalización y de intercambio comercial, iniciados hace siglos, las diferentes unidades de medida que se adoptaron por ciertas civilizaciones o Estados dominantes, están pasando al desuso.
Ya casi ningún infante debe verse sometido al aprendizaje de las equivalencias entre un sistema de medidas y otro. Cuando se habla de una tonelada, casi todo el mundo asume una única equivalencia. Hace apenas medio siglo, había que considerar las variantes de la vara, por citar un caso, y quien sabe cuántas unidades en situación similar. El mundo se ha venido uniformizando cada vez más, aunque pesa aún, mucho, la fuerza de la tradición. Por ejemplo, aunque el metro (m) es la unidad internacional para medir la longitud, el mundo anglosajón insiste en expresar la altura de una persona en pies y pulgadas, así como en América Latina cuantificamos la masa, todavía, en libras y onzas, de origen hispánico.
Empero, con relación a este último ejemplo, aunque decimos «una librita de arroz», al consultar la información en el paquetito, veremos que dice 400 g, que no equivalen exactamente a una libra. En nuestro país está vigente una ley con la que resulta obligatorio para los comerciantes colocar los distintos productos en cantidades que estén expresadas en unidades internacionales, esto es, en las correspondientes al Sistema Internacional de Unidades –SI–, que viene a ser la versión contemporánea del anterior sistema métrico decimal. Sobre el SI, vigente en casi todos los países del mundo, se lee:
El Sistema Internacional de Unidades (abreviado SI, del francés Système international d’unités) es un sistema constituido por siete unidades básicas: metro, kilogramo, segundo, kelvin, amperio, mol y candela, que definen a las correspondientes magnitudes físicas fundamentales y que han sido elegidas por convención. Las magnitudes físicas fundamentales se complementan con dos magnitudes físicas más […] para la medición de ángulos. Por combinación de las unidades básicas se obtienen las demás unidades, denominadas unidades derivadas del Sistema Internacional, y que permiten definir a cualquier magnitud física.
En el Sistema Internacional de Unidades –SI–, se recurre ampliamente al uso de prefijos, que sirven para representar los múltiplos y submúltiplos de las unidades mencionadas en la cita previa. En ese sentido, estamos familiarizados con algunos de ellos: km, mil metros; kg, mil gramos; cm, la centésima parte de un metro. De esta guisa, quedamos claros que el prefijo k, kilo, significa «mil». Anteriormente usábamos la letra K, mayúscula, pero se ha actualizado a la minúscula, para no confundirla con la K de kelvin, el grado absoluto para la medición de la temperatura. También llama la atención que la unidad fundamental SI para la masa no es el gramo (g), sino el kilogramo (kg).
El presente artículo está motivado porque recientemente se han agregado oficialmente cuatro prefijos más a la lista vigente de prefijos pertenecientes al SI. Estos los fija oficialmente la Oficina Internacional de Pesas y Medidas (Bureau International des Poids et Mesures) mediante proceso colegiado de propuesta y convención. Cuando era muy niño, únicamente nos enseñaban submúltiplos desde la milésima, hasta múltiplos de la decena del millar, símbolos aprobados desde 1795, aunque para entonces, desde 1960, se habían aprobado unos que hoy en día no nos parecen extraños, debido a su uso en informática: M para mega, un millón (106); G para giga, un millardo, o mil millones (109) y T para tera, un billón, o un millón de millones (1012).
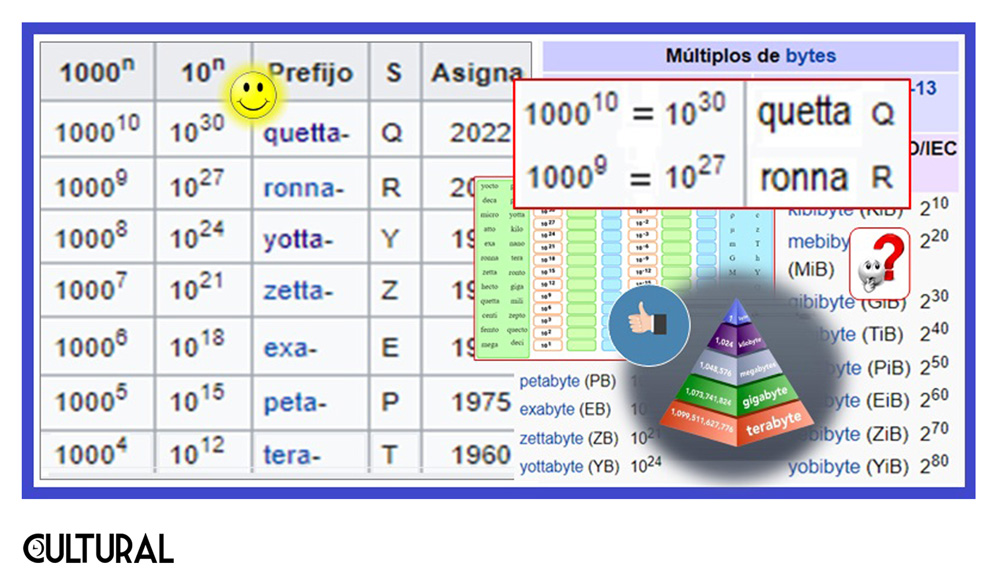
En aquellos entonces, en la infancia, se usaba D, para deca (101 = 10); H, para hecto (102 = 100); K, para kilo (103 = 1000) y Ma, para miria (104 = 10,000). El último (miria) pasó al desuso, y como hemos hecho ver con el símbolo para el prefijo «kilo», se modificó, al igual que los otros, pues deca se simboliza por da, y hecto por h, también minúscula. Como es razonable, los múltiplos, al igual que los submúltiplos, los fraccionamientos, van de 10 en 10 por tratarse de un sistema decimal, acorde al sistema decimal que utilizamos a nivel mundial.
En la imagen siguiente, al centro, aparecen los primeros prefijos, de fines del siglo XVIII, posiblemente más conocidos, y dos de los agregados en la convención de 1960: micro (µ) para millonésima (10–6), y mega (M) para un millón (106). También, como fondo, se muestra parte de un agradable ejercicio, que puede encontrarse en este enlace, en el cual se pide que se coloque el nombre y símbolo de los 24 prefijos actualmente en uso, incluyendo los cuatro nuevos: ronna y ronto, quecto y quetta. Estos prefijos abarcan desde el pequeñísimo submúltiplo de 10–30, que es quecto, hasta el múltiplo mayor, que es quetta, equivalente a un inmenso 1030 (léase un 1 seguido de treinta ceros).
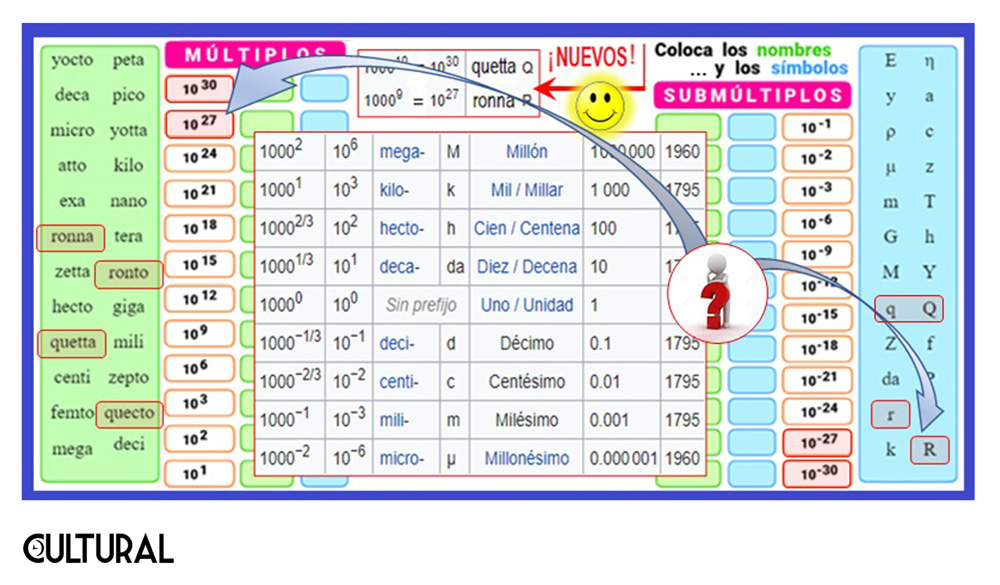
En el ejercicio mostrado, sin mayor información, podemos imaginar un esfuerzo de memoria, clásico del antiguo concepto del estudio, como si se tratara de un trabajo «bancario» de memorización. Sin embargo, como pasaremos a ver en lo que sigue, se trata de comprender el significado de los prefijos, lo que ayuda grandemente a recordarlos, como recurso mnemotécnico. También será pertinente ver el por qué estos corresponden a exponentes múltiplos de 3 (i.e. van de 3 en 3) y qué relación guardan con la informática y el sistema binario de numeración, utilizado por los computadores actuales, los ordenadores electrónicos digitales.
Abrimos el tema hablando del conteo y de la medición como los primeros procesos matemáticos llevados a cabo. Enfatizamos el proceso de construcción de un lenguaje apropiado, que permita sistematizar los procedimientos. Para facilitar las comparaciones y manejo de cantidades diversas, el particular uso de apropiados múltiplos o submúltiplos es altamente conveniente. Con la uniformización que actualmente se está llevando a cabo, vemos que algunas magnitudes ya se están midiendo, casi exclusivamente, en las mismas unidades de medida.
Para cualquier magnitud de la que se trate, hay cantidades muy pequeñas y otras muy grandes, de forma que, para usar una misma unidad de medida, se hace necesario recurrir a la notación científica, basada en potencias de 10, dado que nuestro sistema de numeración es decimal, de base 10. Por ejemplo, es posible expresar la masa de objetos tan distintos, en la misma unidad. Es el caso de la masa del planeta Tierra y la masa de un electrón, ambas expresadas en kilogramos (kg). También es frecuente utilizar unas cuantas cifras significativas, de manera que, usando múltiplos, o submúltiplos, de potencias de 10, podemos manejar fácilmente todos los valores.
Ilustremos el punto. Si la distancia de la ciudad de Guatemala a Xela es de 200,000 m aproximadamente, afirmamos, de manera más asequible, que la distancia es de 200 km, pues 1000 m = 1 km. Esta cantidad puede ser expresada de muchas maneras equivalentes: 200 km = 200 x 103 m = 2 x 105 m. Sobre la lectura de las cantidades, tanto en la llamada cuenta corta, que vemos en el idioma inglés, como en la cuenta larga, que usamos en el castellano, los números se separan en períodos de tres cifras. En el artículo «Los millares: una problemática convencional», explicábamos las razones por las cuales esta elección no es computacionalmente la más acertada.
Lo importante es que, debido a esta forma de lectura, de tres cifras en tres cifras, en ingeniería, y otras áreas de aplicación cuantitativa, se volvió frecuente utilizar como exponente de la notación científica un múltiplo de tres. De ello que, para los múltiplos después del millar y los submúltiplos debajo de la milésima parte, se puso en práctica el uso de prefijos que van de mil en mil, es decir, de 103 en 103. Veamos un ejemplo que explique esto que estamos apuntando. En nuestro artículo previo, «Nuestro sistema estelar», recurrimos a la llamada unidad astronómica, que es la distancia media entre la Tierra y el Sol.
En términos numéricos, desde la asamblea general de la Unión Astronómica Internacional, celebrada en Pekín, en agosto de 2012, una unidad astronómica equivale exactamente (por definición) a 149 597 870 700 m. Así, utilizando únicamente seis cifras significativas: 1 ua ≃ 149 598 000 000 m = 149 598 000 km = 149 598 Mm = 149.598 Gm = 149.598 x 109 m ≃ 149.6 Gm. Vemos que podríamos recordar la cantidad en metros (m), en kilómetros (km), en megámetros (Tm) en gigámetros (Gm) o en cualquier otro múltiplo de la unidad elemental, el metro, pero, ciertamente, pensar en 149.6 Gm se hace más fácil de recordar.
El título de hoy responde a los nuevos prefijos que han sido definidos en la Conferencia General de Pesas y Medidas (Conférence générale des poids et mesures, CGPM), la número 27, celebrada a mediados de este mes de noviembre. Quetta, ronna, quecto y ronto fueron aprobados en esta última CGPM, para agregarlos como prefijos válidos en el SI. Los prefijos quetta (Q) y ronna (R) son los correspondientes a los múltiplos equivalentes a 1027 y 1030, respectivamente, mientras sus contrapartes hacia lo pequeñísimo, ronto (r) y quecto (q) para los submúltiplos de 10–27 y 10–30 e ese orden.
Antes de esta, se aprobaron los otros prefijos en las conferencias previas de 1960 y 1975, además de la celebrada en 1991. Curiosamente, estos múltiplos fueron incorporados por las necesidades que en el mundo de la computación y el emergente big data aparecieron. Cuando hablamos de los números grandes,hicimos ver que el mundo físico tiene sus límites, es decir, hacia lo pequeño, o hacia lo muy grande, el mundo físico presenta límites. Por otro lado, el mundo computacional, de la combinatoria y de la generación de información, pareciera no tenerlos. Piénsese que el número de electrones existentes en todo el cosmos se estima en inferior a 1080, mientras las permutaciones de 70 elementos superan el googol = 10100, pues: 70! > 10100.
Antes decíamos kilo y por lo usual pensábamos en un kilogramo. Ahora sabemos que es mil. Cuando decimos mega, giga o tera, como cuando aseveramos: «está muy pesado y quizá sean muchos megas para enviártelo; quizá llegue a más de un giga», estamos comiéndonos el byte, así como antes nos comíamos el gramo. Pesa tres kilos, decíamos, sin vincularlo a kilómetro. Hoy decimos, me compre un externo de 2 teras, y nadie lo vincula con terámetro (Tm). Esto lo comentamos, pues la circunferencia terrestre mide 40 Tm = 40,000 km = 40 x 106 m, mientras la distancia Tierra-Luna es de 384 Tm, y en estas situaciones usamos el prefijo tera.
Para comprender esta vinculación con el sistema binario, y el uso de los prefijos mega, giga, tera, etcétera, requeriríamos de un conocimiento básicos del sistema binario de numeración. En el artículo «Sistemas de numeración» hicimos una breve introducción al tema:
La base de un sistema de numeración posicional puede ser cualquier número natural superior a uno, es decir, de dos en adelante [, indicando] cuántos números pueden ser representados en la posición de las unidades [, y coincidiendo] con el número de guarismos que se emplean. […] Estamos familiarizados que 23 vale veintitrés, porque en el sistema decimal dos unidades de segundo orden valen 20 (2 x 10), por lo que 23 = 2 x 10 + 3 x 1 = 20 + 3 = 23.
Sin embargo, en otro sistema que admita los signos 2 y 3, 23 significa exactamente 2 unidades de segundo orden sumadas con 3 unidades de primer orden. Así, en la base cinco [, como ejemplo,] 23 equivale a dos unidades de segundo orden, o sea 2 veces cinco, sumado con 3 unidades simples, de valor uno. En otras palabras, tenemos que, en base cinco: 23cinco = 2 x 5 + 3 x 1 = 10 + 3 = 13diez.
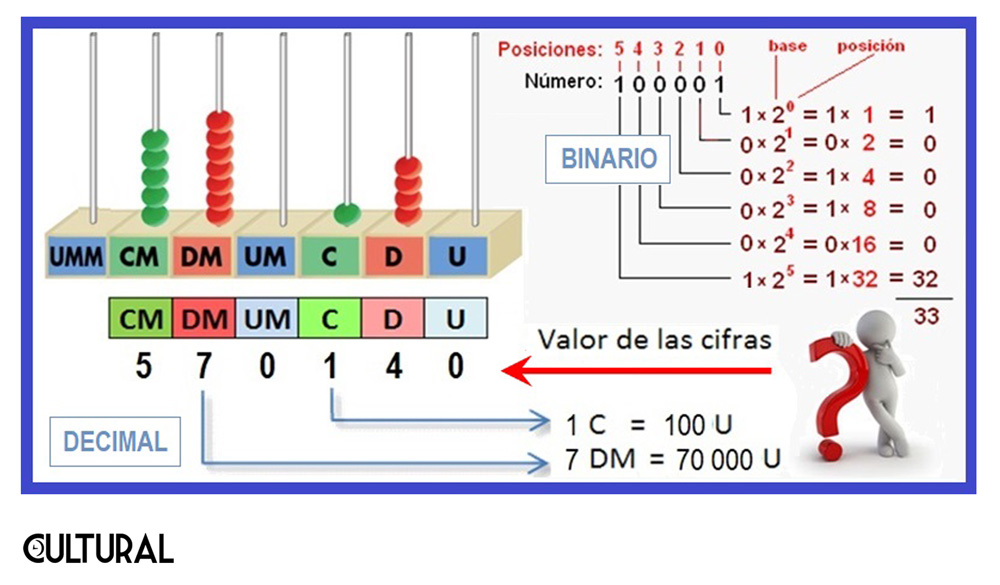
En este sentido, el sistema más simple, el que utilizan los ordenadores electrónicos es de base dos, básicamente porque los autómatas electrónicos reconocen dos estados electromagnéticos, uno alto y uno bajo, lo que da origen a los dos modos de representación, conocidos con dígitos binarios, o bits: 0 para el bajo y 1 para el alto. La expresión bit es una contracción anglosajona, un acrónimo, de la expresión binary digit. En la imagen previa, en la derecha, se observa la representación del número decimal 33.
Sobre el sistema binario y los usos, escribíamos en «Modelaje desde los datos», lo siguiente:
Conviene aclarar qué significan estas unidades utilizadas para la medición del volumen de información. El byte (B) es la unidad elemental de información utilizada en computación y en telecomunicaciones, equivalente, en pocas palabras, a un conjunto ordenado de ocho bits, razón por la cual, en otros idiomas, incluidos el castellano, se le conoce también como octeto. Amerita adentrarnos en la historia del uso de esta unidad fundamental, pero por ahora baste saber que un exabyte (EB) es equivalente a 1018 bytes. ¿Y esto cuánto es? Perdemos un poco la noción del tamaño de cantidades muy grandes cuando nos vemos en la necesidad de utilizar escalas geométricas. Por eso conviene pasar las cantidades a equivalentes físicos.
Como estamos señalando, en nuestro lenguaje coloquial, solemos hablar de gigas (1 GB = 109 bytes) y teras (1 TB = 1000 GB = 1012 bytes) de información, pero quizá ignoramos que 1 GB de datos equivale, en el sentido físico, a un camión lleno de páginas con texto escrito, y que 1 TB vendría a ser el equivalente a todas las páginas de texto escritas con la materia prima proveniente de 100,000 árboles. Se ha explicado que el peso de todos los datos en Internet a inicios del Y2K era de 1 EB (un millón de TB), habiendo crecido esta cantidad en un factor mayor que mil en tan solo una década.
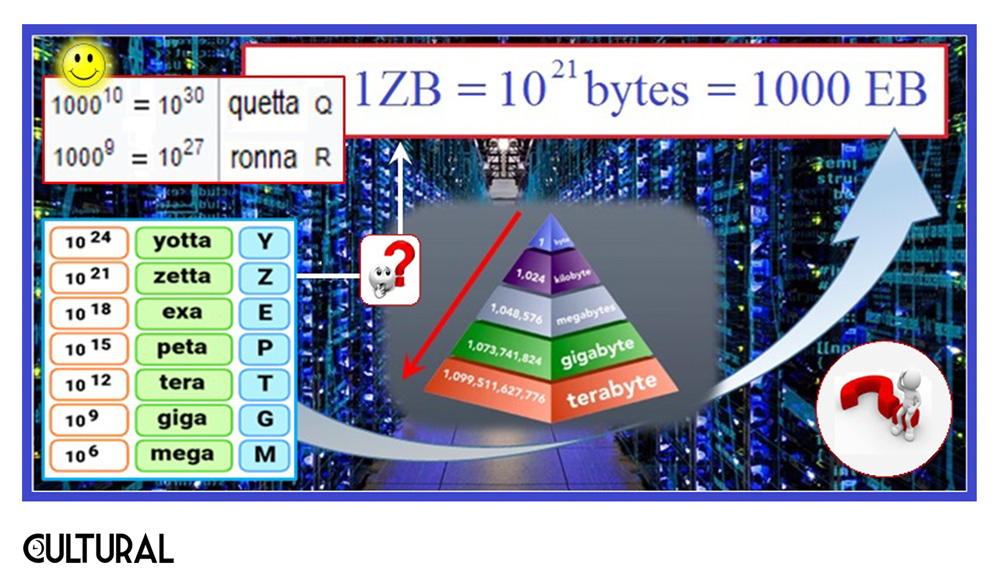
De esta forma, la cantidad circulante en la Internet en el 2015 ya se estimaba superior a varios zettabyte (1 ZB = 1000 TB), lo cual equivaldría a muchos miles de columnas de hojas de papel, colocadas unas sobre otras, tan grandes que cada una llegaría desde donde estamos hasta el mismo Sol. Para visualizar este acelerado crecimiento y las necesidades que hemos dicho llevaron a la creación de ronna y quetta, CISCO ha calculado que el volumen de datos podría duplicarse en menos de un año. Con este cúmulo de zettabytes, llegando pronto al yottabyte, el big data plantea como urgente una nueva forma de procesar la inmensa cantidad de datos que nos está inundando.
Cerramos esta presentación explicando, rápidamente, algo sobre el sentido y significado de los prefijos. Se observará que van en pares, quetta va con quecto, yotta va con yocto, zetta con zepto, para ejemplificar, así que tomemos los múltiplos. Aunque quetta y ronna parezcan los nombres de dos chicas italianas, lo que significan es el número de períodos que se están incluyendo, es decir, cuántos paquetes de tres cifras se incluyen. De las raíces latinas, se puede ver que peta significa cinco, y por ello es 1015 = 10005; exa significa seis, o sea 1018 = 10006; zetta es siete, 1021 = 10007; yotta es ocho, 1024 = 10008; ronna es nueve, 1027 = 10009; y, finalmente, quetta es diez, lo que viene a ser 1030 = 100010.
Finalizamos con una curiosidad incluida en la Wikipedia, con relación a la descripción del nuevo prefijo quetta:
Adoptado el 18 de noviembre de 2022, junto con ronna, ronto y quecto, viene del griego δέκα, deka, que significa diez, pues equivale a 100010 = 1030. Se escogió la letra q como inicial porque no había sido usada antes para otros prefijos o unidades. Inicialmente se consideró nombrar al prefijo «quecca», pero se descartó la idea por su parecido lingüístico a un término vulgar en portugués.
Fuente de imágenes ::
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: https://hardzone.es/tutoriales/componentes/tamanos-memoria-megabyte-gigabyte-terabyte-petabyte/ + https://www.educaplus.org/game/prefijos-del-sistema-internacional-nombres-y-simbolos + https://es.wikipedia.org/wiki/Prefijos_del_Sistema_Internacional
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/Prefijos_del_Sistema_Internacional + https://www.educaplus.org/game/prefijos-del-sistema-internacional-nombres-y-simbolos
[ 3 ] Imagen tomada de gAZeta, editada por Vinicio Barrientos Carles :: https://www.gazeta.gt/sistemas-de-numeracion-ii/
[ 4 ] Imagen tomada de gAZeta, editada por Vinicio Barrientos Carles :: https://gazetagt.com/modelaje-desde-los-datos-ii/ + https://www.educaplus.org/game/prefijos-del-sistema-internacional-nombres-y-simbolos








