Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Las artes son la ciencia de la belleza, las matemáticas son la ciencia de la verdad.
Oscar F. Wilde
El poeta y dramaturgo irlandés Oscar Fingal O’Flahertie Wills Wilde describe, en nuestro epígrafe, la actividad matemática como una búsqueda de la verdad. El excelso filósofo de la Antigua Grecia, Platón, por otro lado, consideraba que lo matemático era lo único perdurable en todas las cosas que alcanzamos a inteligir, lo intrínsecamente inmutable, la esencia de todo cuanto existe. Así, para el fundador de la Academia, por ejemplo, aunque algún objeto pareciera una esfera perfecta, era tan solo el reflejo, imperfecto, de una idea perenne, la esfera, una idea matemática que además de incorruptible era ciertamente inalcanzable, al menos con los sentidos.
Estas nociones se vieron reflejadas en los conceptos griegos de la razón, la episteme, y de la inteligencia, o espíritu, el nous, la parte más elevada de aquello que no es material en la mente humana. De acuerdo con los clásicos, mediante estos elementos las personas podrían, con el entrenamiento apropiado, llegar al conocimiento de la verdad última de las cosas. Fue en la escuela de Pitágoras de Samos en donde se establecieron inicialmente los llamados matematikoi, practicantes, aspirantes al μάθημα (máthēma), el conocimiento más profundo de las cosas. El pensador enseñaba, a su vez, que la μαθηματικά (mathēmatiká – matemática), a diferencia de la μουσική (mousiké – música), requería de un maestro para ser comprendida y aprendida correctamente.
Vemos así que el pensamiento filosófico griego se encuentra bien resumido en lo que Wilde expresa. Lastimosamente, el sistema educativo ha deformado gravemente lo que este ideal implicaba, reduciendo la actividad matemática a la aplicación mecánica de ciertos algoritmos que resuelven determinado tipo de problemas. Consecuencia inmediata de esta reducción de los procesos mentales a unos operacionales, casi irracionalmente automatizados, es que la mayoría de las personas han terminado concibiendo a la Matemática como una colección de fórmulas muertas, y no como un sistema lógico de conceptos racionales, que, en última instancia, pueden ser aplicados de forma práctica. No obstante, el valor de estos sistemas formales no radica en su posible aplicación. Tienen un valor teórico por sí mismos.
Lo conveniente será ejemplificar lo que estamos tratando de explicar. En este sentido, la mejor ilustración podría provenir de cuestiones que podamos visualizar de manera fácil. Por ello estamos recurriendo a lo geométrico, también para insistir que lo matemático no siempre debe incluir los números, al menos no desde un inicio. Geometría significa, casi literalmente, medición de la tierra, pues en griego γῆ – gē es tierra (derivado de la deidad primordial Gea) y μετρία – metría es medida. Esta disciplina matemática dio inicio con el problema práctico de la medición de un cierto terreno. Un caso sencillo de la cuestión proviene de la determinación del área de una porción de terreno de forma rectangular o triangular.
Pues bien, en esta oportunidad traemos a colación el concepto del círculo inscrito. Para ilustrarlo, piénsese en un cuadrado. Si se coloca un círculo en su interior, esto es, que todo el círculo quede contenido adentro del cuadrado, podremos darnos cuenta que, aunque son muchos los posibles circulitos que pueden cumplir con lo solicitado, existe un único círculo interior que es el mayor de todos los otros posibles. Así, dado un cuadrado cualquiera, podemos encontrar el mayor círculo que queda contenido totalmente en este cuadrado, esto es, encontramos el círculo interno maximal, al cual denominamos el círculo inscrito. Véase la imagen, en donde se indican algunos de los conceptos intervinientes.
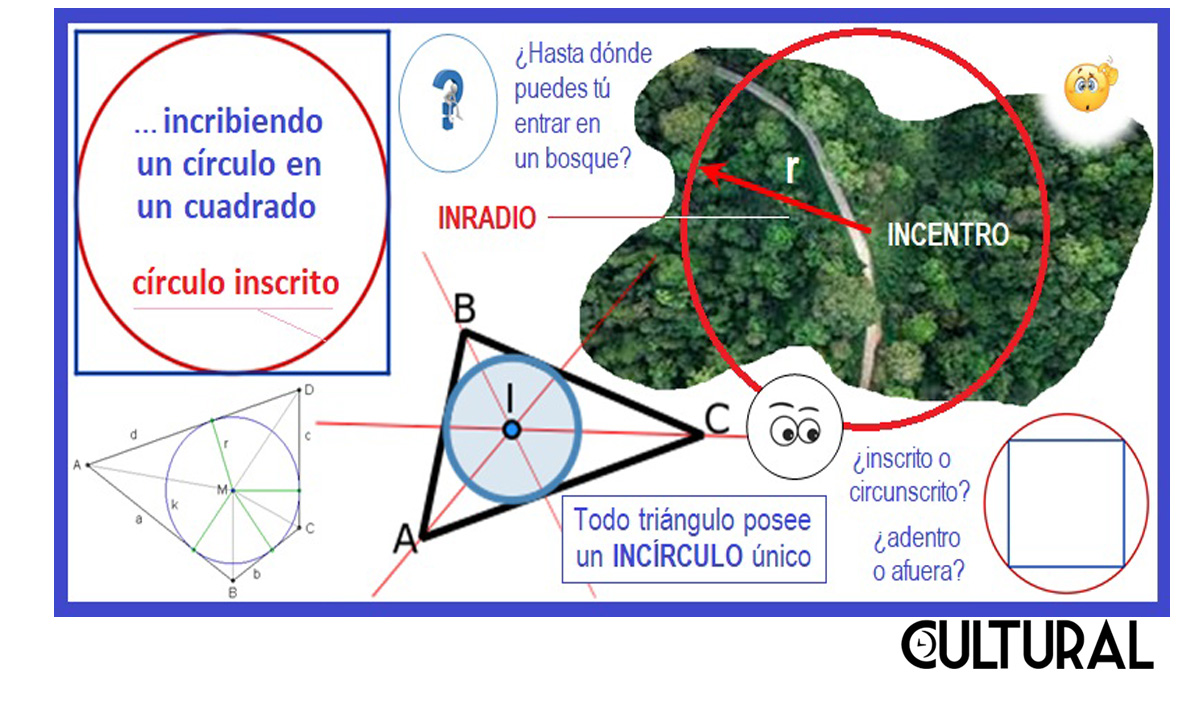
Como se aprecia, de un concepto sale otro relacionado. De una idea se pasa a otra. Así, podemos ir agregando nuevas definiciones, además de las que ya estamos utilizando, de manera implícita, desde el inicio del planteamiento del caso, léase: cuadrado, círculo, interior, etcétera. Por otro lado, podemos observar que este círculo inscrito en el cuadrado, el obtenido del procedimiento anteriormente descrito, resulta tangente a los cuatro lados del cuadrado, esto es, el círculo inscrito y el cuadrado se tocan únicamente en cuatro puntos, cabalmente los puntos medios de cada uno de los cuatro lados del cuadrado.
Si ponemos especial atención, podremos percatarnos que el resultado es único, es decir, dado un cuadrado cualquiera se obtiene un único círculo inscrito en él, o, dicho de otra manera, no puede haber dos círculos inscritos para un mismo cuadrado. También es frecuente identificar a este círculo inscrito como el incírculo del cuadrado. Sin embargo, es notable observar que si intentamos repetir el proceso conceptual con un rectángulo, podremos percatarnos que existe una diferencia substancial al final del procedimiento, y es que el círculo maximal no podrá quedar tangente a los cuatro lados, sino únicamente a tres de ellos, a lo sumo, como se muestra en la imagen siguiente.
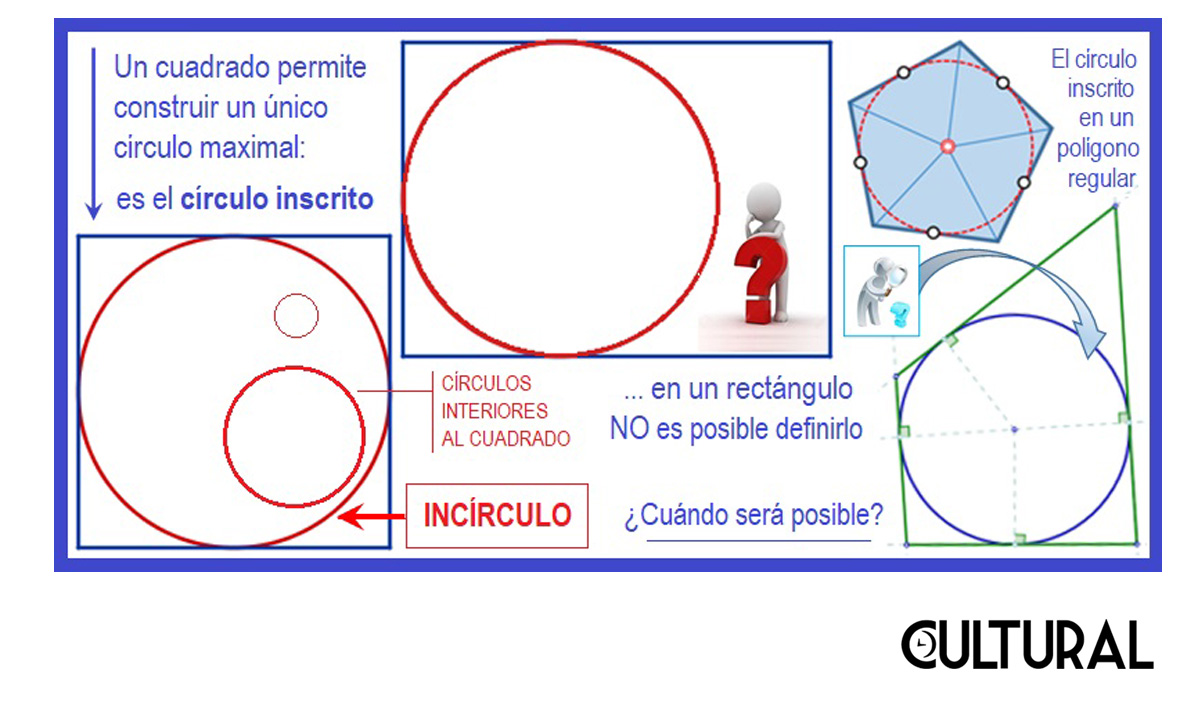
Con este primer concepto, el del titular motivante, una primera problemática está ya esbozada: ¿para qué polígonos podemos encontrar el incírculo? En el fondo de cualquier interrogante, se desarrollan un cúmulo de relaciones, las que pasan a conformar los sistemas formales, objeto de estudio de la Matemática. Hemos podido observar que el incírculo es posible construirlo y definirlo en el caso del cuadrado, pero que para un rectángulo presenta cierta dificultad. El problema matemático es entonces encontrar cuándo se puede replicar el proceso llevado a cabo con el cuadrado, y dar las definiciones pertinentes. Lo importante, matemáticamente hablando, no son los algoritmos, sino los conceptos. En este caso, cuándo es posible hablar del incírculo.
Por otro lado, las definiciones van apareciendo como resultado de este juego exploratorio de ideas. De eso se trata la dinámica intelectual, de nombrar con términos nuevos ciertas situaciones especialmente relevantes que podrían darse, en algunos casos mientras que en otros no. Por ejemplo, caracterizar cuándo existe el incírculo. Una definición, algún objeto matemático nuevo puede fácilmente llevar a otras definiciones. Vienen como «en paquete». En parte, por ello hablamos de un sistema formal, que viene a ser como un combo de objetos y relaciones. Antes de pasar a ver una posible aplicación del incírculo, alguna propiedad interesante, como dice el titular, quiero citar lo que se menciona en la Wikipedia, sobre los polígonos que poseen un incírculo:
En geometría euclidiana, un polígono tangencial, también conocido como polígono circunscrito, es un polígono convexo que contiene una circunferencia inscrita, también llamada incírculo. Esta circunferencia es tangente a cada lado del polígono […] Todos los triángulos son tangenciales, al igual que todos los polígonos regulares con cualquier cantidad de lados. Un grupo bien estudiado de polígonos tangenciales son los cuadriláteros circunscritos.
En lo precedente, hablamos de un círculo inscrito a un cuadrado, pero en la cita previa se menciona la palabra «circunscrito». Aquí vemos un ejemplo de relaciones inducidas, o derivadas, porque, en nuestro caso, si el círculo está inscrito en el cuadrado, entonces el cuadrado estará circunscrito en el círculo. Esto es lo matemático del sistema y de los conceptos mencionados. Es similar a lo que pasa con las relaciones de parentesco. Si A es padre de B, entonces B es hijo o hija de A. Lo mencionamos porque usualmente no pensamos que el concepto de «cónyuge» sea algo matemático. Por ello al inicio hablábamos de nuestra equivocada noción de lo matemático, que creemos que es asunto de solo números.
Si tenemos un incírculo, un círculo inscrito en un cuadrado, entonces el cuadrado en cuestión está circunscrito al círculo. En general, si A está inscrito en B, entonces B está circunscrito en A, y viceversa. Inscrito y circunscrito establecen relaciones inversas, o duales. Lo más importante de la cita previa es que establece el asunto que nos habíamos planteado anteriormente: ¿cuándo un polígono define unívocamente un incírculo? La situación se resuelve con una definición: los polígonos tangenciales son aquellos que poseen un incírculo. Dado un polígono cualquiera, si tiene un incírculo es tangencial, y de manera recíproca, si es tangencial entonces posee un incírculo.
Sin embargo, si se profundiza, se trata de un juego de palabras. Es decir, no hemos dado una caracterización de los polígonos que sí poseerán un círculo inscrito, solo les hemos bautizado: se llaman polígonos tangenciales. Es como definir la maternidad en términos de los hijos. A es madre si y solo si es mujer y existe un B tal que B es hijo o hija de A. Si no sabemos que es «ser hijo/a», no sabremos qué es ser madre, y de manera recíproca igual. Podemos definir un concepto en términos de otro. El concepto primario, del que hablamos primero, se denomina primitivo, mientras que el otro, el que se deriva del anterior se llama concepto secundario.
Únicamente se definen los conceptos secundarios, y se definen en términos de los conceptos u objetos primitivos. También podemos notar que se habló de una «circunferencia», y aunque, como legos no distinguimos cuando alguien nos menciona un círculo o una circunferencia, en Matemática es fundamental ser riguroso con el uso de los términos. Esta es otra característica del quehacer matemático. En la Matemática, como constructo, y, en general, en todas las ciencias formales, se pone mucha atención al uso lenguaje; algunos piensan que se trata el lenguaje mismo. Por círculo se entiende el disco, la superficie, esto es, el interior de una circunferencia, mientras que esta última es la frontera, la línea que sirve de borde para un círculo.
Para reforzar la idea, debemos tener claro que la circunferencia tiene una longitud, mientras que el círculo tiene un área, porque es una región del plano, mientras que la circunferencia es una línea. Regresando a la cita, se mencionó que «Todos los triángulos son tangenciales, al igual que todos los polígonos regulares con cualquier cantidad de lados». Es decir, cualquier triángulo, o cualquier polígono regular, tiene un único incírculo. En el caso de los cuadriláteros es distinto. Ya mencionamos que el cuadrado tiene incírculo, pero el rectángulo no (asumiendo que tiene los lados de diferente tamaño).
En efecto, los cuadriláteros tangenciales, en los que es posible definir un incírculo de manera única, ha sido estudiados ampliamente; se les denomina cuadriláteros circunscritos. La caracterización es muy interesante, y con toda seguridad regresaremos a ella en próxima oportunidad. Por ahora, solo la mencionamos: para que un cuadrilátero sea circunscrito (esto es, tangencial) se requiere que tenga dos pares de lados opuestos que sumen igual. Esta caracterización es de doble vía. Si tiene un par de lados opuestos que sumen igual, entonces es tangencial y posee incírculo. Si posee incírculo, entonces tendrá dos pares de lados opuestos que suman igual.
Nótese que se llaman cuadriláteros circunscritos porque poseen un círculo inscrito, pues el círculo está inscrito en el cuadrilátero, pero el cuadrilátero circunscribe al círculo. Como conceptos derivados tenemos que el centro y el radio del incírculo, cuando este existe, se denominan incentro e inradio respectivamente. También podríamos hablar de la incircunferencia, o circunferencia inscrita. Nótese que un círculo en el plano está perfectamente determinado por su centro y su radio, o por su circunferencia. Esto es, si establecemos cuál es su centro y cuál es su radio, determinamos totalmente el círculo.
Y aquí podemos pasar rápidamente a la aplicación, la que hemos calificado de «una interesante propiedad». Resulta que, en las situaciones en las cuales existe el incírculo de un polígono, es decir, cuando se trata de un polígono tangencial, tenemos que el área del polígono será el producto del semiperímetro y el inradio, o, dicho de otra forma, será la mitad del producto del perímetro por su inradio. Esto quiere decir que, de alguna forma, las dos dimensiones de un polígono plano están representadas, y quedan determinadas, por dos parámetros, a saber: la medida de su borde, el perímetro, y la medida de su «profundidad» intrínseca, que viene a ser el inradio.
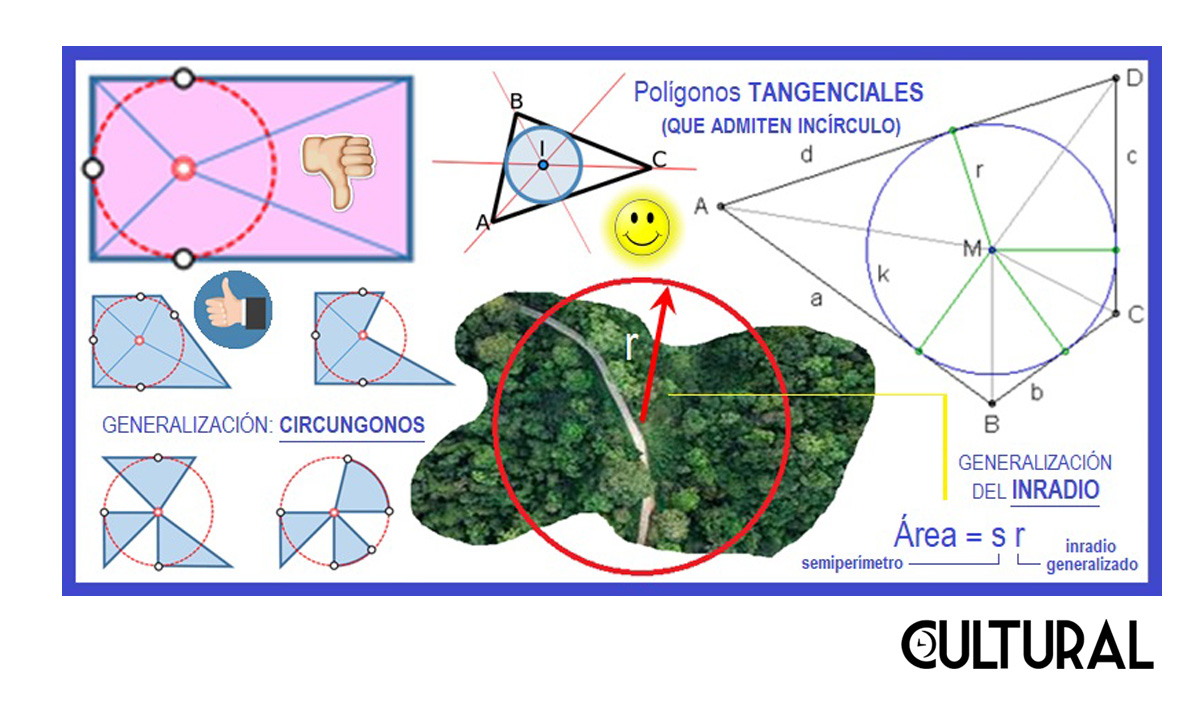
Dicho de otra manera, si nos preguntaran por el tamaño de un cierto polígono, aunque tuviera muchos lados, si este fuera tangencial (o sea, si existe el incírculo), bastaría con conocer cuál es su periferia, es decir, cuánto mide su frontera, o perímetro, y cuál es su profundidad, que vendría dada por el radio del incírculo en cuestión. Como otra característica de la Matemática es su gran potencia, y su tendencia, a la generalización, aunque el incírculo no existiera, como lo hemos planteado es plausible, siempre sería posible conocer el tamaño del mismo, el inradio, pues vendría dado por esta relación que estamos planteando: Área = ½ p r = s r (semiperímetro x inradio).
Cerrando, ahora podrías decirle a tu pareja: «estamos en una relación matemática». Si no, díselo a un amigo, pues la amistad es simétrica, si A es amigo de B, B será amigo de A. No podríamos usar el término amistad si no fuera así. Empero, la amistad no es transitiva. En fin, nuestro objetivo ha sido hacer un poco de rompehielos, para continuar luego conversando sobre estas ideas y su importancia en nuestra vida cotidiana. Para la próxima, estaremos adentrándonos en el caso de incírculo de un triángulo, que, como hemos mencionado, siempre existe. Para ello hablaremos del insigne ingeniero y matemático helenístico, Herón de Alejandría, destacado en la provincia romana de Egipto, a quien se atribuye un importante teorema.
Fuente de imágenes ::
[ 1 + 2 + 3 ] Imágenes editadas por Vinicio Barrientos Carles, tomadas parcialmente de las siguientes fuentes :: https://es.wikipedia.org/wiki/Circungono + https://es.wikipedia.org/wiki/Cuadril%C3%A1tero_circunscrito + https://es.wikipedia.org/wiki/Incentro + https://es.wikipedia.org/wiki/Pol%C3%ADgono_tangencial








