Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
En el círculo se confunden el principio y el fin.
Heráclito de Éfeso
En el artículo precedente, «Cavalieri y el desplazamiento paralelo», presentamos rápidamente cómo es posible lograr la noción de espacios de distintas dimensiones, diferentes al tridimensional estándar, por medio de un proceso proyectivo, el cual permite reducir la dimensión del espacio original mediante cortes, que generan secciones, o aumentarla, mediante desplazamientos de traslación. Así, ejemplificando, al tomar un cuerpo 3D, tridimensional, como el prismatoide en la izquierda de la imagen que sigue, distintos espacios 2D, planos, generarán objetos bidimensionales por medio de los cortes seccionales correspondientes, que aparecen en la ilustración simbolizados por S1, S2 y S3.
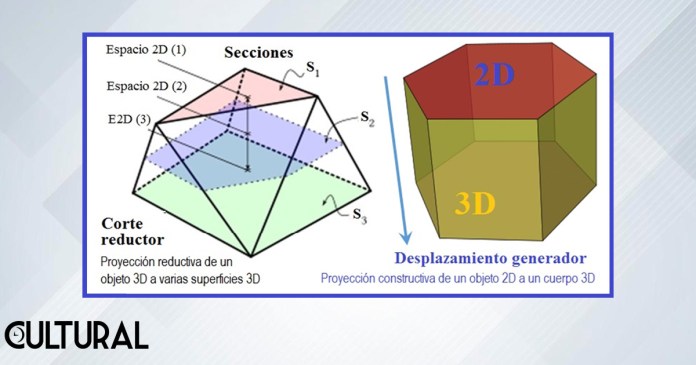
De similar manera, si procedemos análogamente, pero partiendo de un objeto 2D, plano, o de una línea 1D, unidimensional. Este proceso reductivo nos posibilita concebir objetos en En, cuando n < 4. En forma conversa, recíproca. también es posible ampliar la dimensión de un objeto en En. Para ello, podemos proyectar el objeto original por medio de un desplazamiento ortogonal, o en una dirección «linealmente independiente» a las ya consideradas en el objeto inicial, como puede verse en el ejemplo a la derecha de la imagen siguiente, donde, partiendo de un objeto 2D, un hexágono, se ha generado un objeto 3D, un prisma tridimensional de base hexagonal.
Con este segundo proceso proyectivo es posible construir objetos desde la dimensión más baja, en cuyo caso generaremos, sucesivamente, por desplazamiento ortogonal, una secuencia de cuerpos en cada uno de los espacios euclídeos n – dimensionales En. Estos objetos o cuerpos n – dimensionales se llaman denominan hipercajas, n – ortótopos o rectángulos n – dimensionales. Cuando una hipercaja es tal que la longitud de cada uno de los desplazamientos generadores es el mismo, es decir, que las medidas de sus lados son iguales entre sí, se dice que se trata de un hipercubo, o cubo n – dimensional.
El término polítopo de medida se utilizaba antes para designar un hipercubo unitario, es decir un n – cubo cuyo lado tenía una longitud unitaria, esto es, de medida igual a uno. Así, el volumen de una hipercaja puede ser definido como el número de hipercubos unitarios que contiene, lo cual a su vez puede ser calculado, fácilmente, como el producto de los n valores de las medidas de sus correspondientes lados, para cada una de las n – dimensiones que constituye la hipercaja. La denominación de polítopo de medida proviene del notable trabajo del geómetra canadiense H. S. M. Coxeter, hace ya más de un siglo.
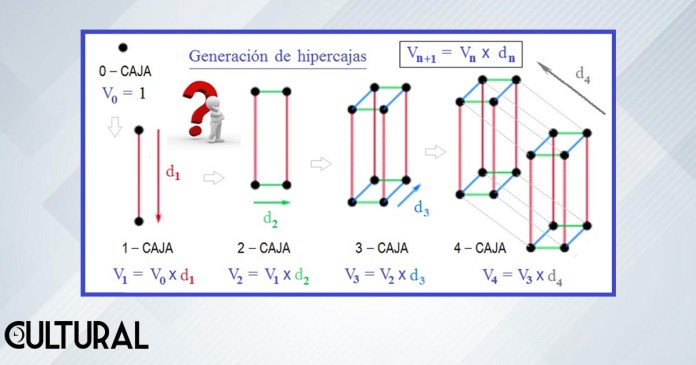
Las primeras hipercajas, es decir, para las primeras dimensiones, se muestran en la imagen precedente, desde n = 0 hasta n = 4, aunque en este último caso se recurre un tanto más a la imaginación. También debe notarse que la definición del volumen o tamaño de una hipercaja es ciertamente inductiva, como puede verse en la imagen previa.
Lo anterior significa que, partiendo de un volumen unitario (V0 = 1) y planteando que el volumen de la (n + 1) – caja, obtenida del desplazamiento de otra n – caja de tamaño Vn, se obtiene multiplicando este volumen originario por la longitud del desplazamiento dn, se tiene que: Vn+1 = Vn x dn. De esta guisa, para cualquier m natural, m ∊ ℕ, se tiene que: Vm = d1 x d2 x d3 x… x dm, como sucede en la geometría euclidiana, para los particulares casos con m < 4.
Ya habiendo definido el volumen o tamaño de una caja en cualquier dimensión, es posible desarrollar un proceso formal seguro mediante el cual sea factible la determinación del volumen otros cuerpos n – dimensionales. También hemos mencionado previamente que la teoría de la medida es la rama de la Matemática que se encarga de estos procesos formales, y entre otras cosas permite desarrollar el concepto de la medida de un conjunto y de las funciones denominadas medibles, con las cuales se pasa al estudio del proceso de integración, iniciado desde los tiempos antiguos por el método de exhaución, presentado brevemente en artículos al respecto de la obra y aportes de Arquímedes de Siracusa, inventor del método.
Técnicamente, de manera más formal, una medida es una función que asigna un número real extendido no-negativo (R+* = [ 0 , +∞ ]) a ciertos subconjuntos del espacio euclidiano En, o de forma más general, subconjuntos de un espacio E, denominado un espacio de medida. Esta función de medida debe satisfacer algunas propiedades fundamentales, entre las que destaca el axioma contable aditivo, que de manera simplificada implica que la medida de un «conjunto grande» puede ser expresada como la suma de las medidas de unos «subconjuntos más pequeños», en los cuales se ha particionado el conjunto original, siendo esta descomposición de tamaño contable. Este «tamaño contable» se refiere a que el número de partes es finito o a lo sumo infinito numerable, en su cardinalidad.
En el caso estándar, los subconjuntos componentes en los que se subdivide un conjunto cualquiera son cabalmente las hipercajas que estamos presentando, o bien n – prismas, como cuando se consideran delgadísimos discos, n – cilindros de altura infinitesimal. Este segundo caso ha sido ya exhibido en varios artículos previos en estos Suplementos Culturales LaHora, como en los casos del cálculo del volumen de un cono o de una esfera tridimensional. Lo interesantísimo de este proceso de sumación es que puede ser extendido de manera consistente a cualquier otro espacio En, de manera que el volumen Vn de un determinado cuerpo n – dimensional resulta bien definido. Este proceso matemático de sumación contable se conoce como integración, estudiado en el cálculo infinitesimal.
A pesar de lo intuitivo de los procesos aquí descritos, los aspectos matemáticos teóricos son importante y necesarios, para evitar las posibles contradicciones o paradojas, tales como la citada paradoja de Banach – Tarski, planteada, precisamente, por los matemáticos polacos Stefan Banach, destacado en Análisis Funcional, y Alfred Tarski, destacado en Lógica. La teoría permite demostrar que, bajo los supuestos definitorios de una función de medida cualquiera, sin importar cual sea específicamente, se tendrán siempre subconjuntos del espacio que no serán medibles bajo la función asumida, por lo que las operaciones usuales de adición de volumen no serán posibles, en vista de que el volumen de estos conjuntos de puntos resultará imposible de obtener.
La verdad es que estos conjuntos no medibles, aunque parezca extraño, no solo existen, sino que son abundantes, al considerar todos los arreglos de puntos posibles. Estas formalizaciones matemáticas requirieron, históricamente, de varios siglos de arduos trabajos, de manera que no podemos concebirlas como inmediatas o carentes de una evolución teórica muy interesante, digna de su meritorio estudio. Sin embargo, de suerte que nuestras hipercajas no solo son intuitivas, sino que siempre serán fácilmente medibles, por lo que constituyen el pilar de la medición de cualquier objeto n – dimensional estándar.
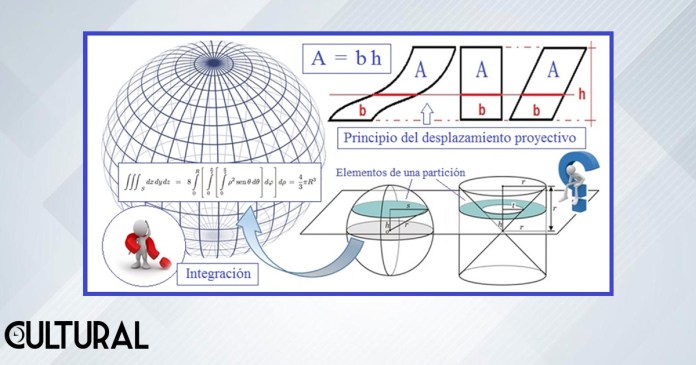
Se ha mencionado a los n – prismas, los cuales de manera sencilla pueden ser visualizados como el desplazamiento, ortogonal u oblicuo, de un cierto cuerpo (n – 1) – dimensional, que pasa a constituirse en la base B del prisma. Así, la base B, existente en la dimensión n – 1, es proyectada por desplazamiento o traslación en una dimensión extra, generando un cuerpo n – dimensional, justamente el n – prisma de base B. Aunado a este proceso de ampliación dimensional, hemos anotado que el volumen del n – prisma será la medida (volumen o tamaño) de la base B multiplicada por el tamaño (longitud) del desplazamiento.
Este proceso viene a generalizar el principio de Cavalieri, precedente del cálculo integrodiferencial de Isaac Newton y de Gottfried Leibniz, del cual hemos realizado una primera aproximación en el artículo previo. En particular, los cilindros son prismas de base «redonda», por lo que, si conocemos el volumen de su base, podremos calcular el volumen del cilindro. Conviene reparar que aquí el término «volumen» hace referencia a una medida del tamaño del cuerpo, y no únicamente en el sentido del espacio tridimensional que ocupa un sólido, como es usual comprender.
Por otro lado, nótese que en lo previo se ha realizado una presentación de los cuerpos más simples que pueden ser construidos en un espacio euclídeo n – dimensional En, a saber, las denominadas hipercajas en n dimensiones o n – rectángulos. P ara ello se hizo mención de un proceso proyectivo de doble vía, sea para aumentar en uno la dimensión de un objeto, o sea para reducirla, también en una unidad. Básicamente, podemos generar objetos en una dimensión menor realizando cortes o secciones, es decir, intersecciones con espacios afines (n – 1) – dimensionales, reducidos en una unidad del espacio donde el objeto original está incrustado. Empero, hay otras relaciones que vale la pena comentar. Véase la imagen que sigue.
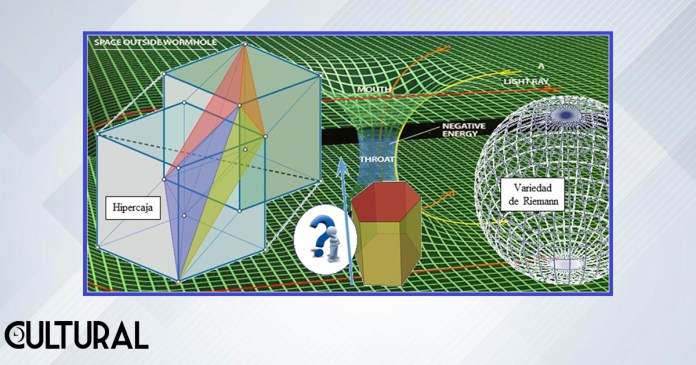
El ejemplo clásico puede construirse si se toma un cubo o una caja tridimensional cualquiera y se realiza un corte imaginario con un plano transversal, 2 – dimensional, obteniendo un polígono que ya no es una caja tridimensional, sino un objeto bidimensional. En particular, si los cortes son paralelos a las bases de una 3 – caja, entiéndase una caja en el sentido coloquial, un paralelepípedo, se obtendrá una 2 – caja, es decir, un rectángulo.
De manera conversa, un proceso inverso puede generar un objeto (n + 1) – dimensional partiendo de otro existente en En, es decir en n dimensiones. Esto es posible si realizamos un desplazamiento paralelo unidireccional, como cuando al tomar un rectángulo, una 2 – caja, lo trasladamos ortogonalmente, perpendicularmente, para obtener una 3 – caja, un paralelepípedo.
Los procesos descritos en el párrafo anterior son fáciles de visualizar, esencialmente porque las dos y tres dimensiones nos parecen más que geométricamente intuitivas, siendo, sin embargo, este proceso generalizable, mediante abstracción, a un número natural arbitrario n, en un espacio euclídeo En cualquiera. Por medio de este proceso de desplazamiento, traslación en una dimensión imaginaria extra. es que anteriormente pudimos definir, de manera totalmente intuitiva, lo que es un prisma, el cual no sería nada más que el objeto (n + 1) – dimensional obtenido del desplazamiento de un objeto previo n – dimensional, al cual pasamos a denominar la base del prisma construido.
De hecho, hemos ido aún más lejos, al afirmar un hecho substancial, que es que el volumen, o medida del tamaño, de este (n + 1) – prisma construido mediante este procedimiento vendría dado por el producto del volumen, la medida del tamaño, del objeto base, n – dimensional, por la longitud del desplazamiento, tal y como se ilustra en la imagen siguiente, en la que se observa un 3 – prisma generado por la traslación de una base bidimensional, que en este caso es un 2 – polítopo, polígono plano. Este hecho fundamental referidos al volumen de los 2 – prismas se ilustra, como puede apreciarse, en la imagen que sigue.
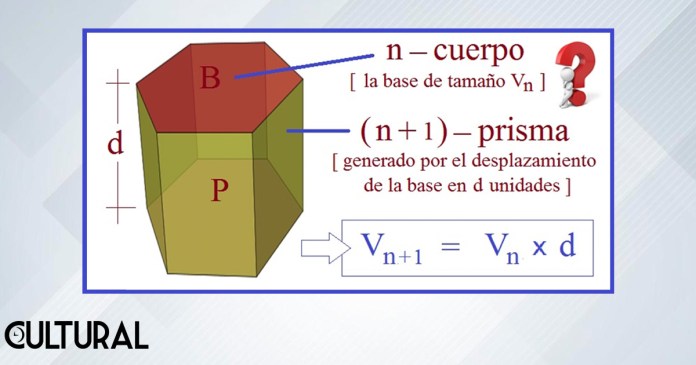
También mencionamos, rápidamente, que si la base del prisma en cuestión fuera redonda, un círculo, por ejemplo, al prisma suele llamársele un cilindro. En la presente oportunidad estamos abordando el tema de esta «redondez» de un cuerpo, que está perfectamente dibujada en nuestra mente a través de la imagen circular, la cual en tres dimensiones nos conducirá a la esfera, uno de los objetos más primitivos que geométricamente nos podemos plantear. Todos, desde muy pequeños, estamos familiarizados con una pelota, y la redondez perfecta de una bola no puede ser sino fascinante para cualquiera. Esta redondez, o circularidad, viene a ser el segundo propósito de la presente publicación.
Empero, cabe perfectamente preguntarse, ¿cómo podemos definir matemáticamente esta redondez?, denominada simetría radial, en vista de que, partiendo desde su centro, una esfera no distingue dirección alguna (isotropía física). Por otro lado, una esfera, por citar el caso tridimensional, no se distingue de otra, sino es por su tamaño, determinado por su diámetro. o su radio, si se prefiere, de forma tal que todas las esferas son «similares», homogéneas, ciertamente proporcionales en algún factor lineal. Podemos resumir diciendo que todas las esferas son geométricamente equivalentes, isomorfas.
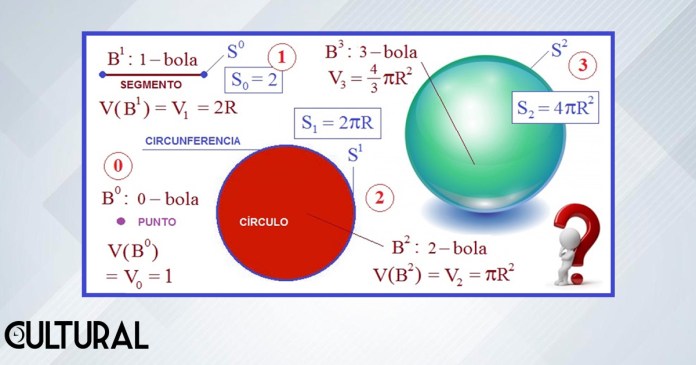
La noción de una posible generalización de lo que el círculo o la esfera son en dos y tres dimensiones, proviene, probablemente, de la geometría analítica, propuesta e iniciada hace varios siglos por el matemático y filósofo francés René Descartes, con la cual se inició el estudio de una correlación entre la geometría euclidiana y el álgebra incipiente de los tiempos posrenacentistas. Fundamentalmente, explicándolo de manera sucinta, se describe las figuras en el plano por medio de las ecuaciones que satisfacen las coordenadas de los puntos de los distintos lugares geométricos, estableciendo una relación de dos vías entre las ecuaciones algebraicas, de las coordenadas de los puntos, y las figuras u objetos conformados por el conjunto de los puntos que satisfacen las ecuaciones dadas.
Así, los puntos de una circunferencia cumplen con ser equidistantes del centro, es decir que una circunferencia es el conjunto de puntos que guardan una misma distancia, el radio r, de un punto fijo llamado el centro de la circunferencia. Usando el concepto de métrica, o distancia entre puntos, la anterior definición geométrica se traducirá en una ecuación que establece eso precisamente. Si el centro está en el origen del plano, los puntos P(x,y) estarán en la circunferencia de radio r, si y solo si las coordenadas (x,y) del punto P satisfacen que: x2 + y2 = r2.
Con esta nota, podemos fácilmente pasar a puntos n – dimensionales que posean n coordenadas cartesianas (x1, x2, x3,… xn) y solicitar que se cumpla la condición siguiente: x12 + x22 + x32 +… xn2 = r2. En este momento cabe realizar una observación, muy del caso: en el lenguaje coloquial no solemos distinguir entre una circunferencia y un círculo. Lo cierto es que la circunferencia es el borde, o frontera, de un disco, mientras que el círculo es el interior o «relleno» del disco. Así, la circunferencia es un objeto lineal o 1 – dimensional, mientras que el círculo es un objeto 2 – dimensional, plano o bidimensional. La frontera de un conjunto u objeto es un concepto primario den la Topología General o Topología de Puntos.

Dicho de otra manera. la circunferencia es la frontera de un círculo, y tiene una por medida una longitud, mientras que el círculo es el interior de una circunferencia, por lo que tiene por medida un área, o medida de superficie. En el caso tridimensional existe menos consenso, aún entre matemáticos, pues unos, los geómetras, denominan esfera al cuerpo tridimensional, mientras que otros, los topólogos suelen usar el término para referirse a la frontera, es decir, a la superficie esférica, que es bidimensional.
Sin entrar en honduras terminológicas (que seguramente pueden provocar confusión), aquí nos referimos al interior como una bola, y a la frontera como una esfera, o bien, en la generalización para el espacio euclidiano En, n – dimensional, hablaremos de una n – bola para el cuerpo «relleno» y de una hiperesfera para las fronteras correspondientes a estas n – bolas.
Sin embargo, en importante notar que una 3 – bola, B3 (la esfera tridimensional sólida), tiene por frontera una superficie bidimensional, que es la superficie esférica usual, a la que denominamos S2, la cual es una variedad riemanniana de dos dimensiones, incrustada en el espacio E3 (nuevamente aquí, a S2 los topólogos le llaman la 2 – esfera, porque es bidimensional, mientras que los geómetras le llaman 3 – esfera, por ser un conjunto de puntos en E3).
Curiosamente, aunque la distancia euclidiana usual utiliza el exponente 2 en su cálculo, es factible cambiar tal exponente por otro valor numérico, lo cual origina una métrica diferente, pero viable. Una de las propiedades que se pierde es la isotropía, que hemos introducido como la originaria de la idea de «redondez» en Sn. Finalmente, basados en la definición analítica previa y conforme la teoría de la medida básica, es posible determinar el volumen que una cierta n – bola encierra, V(Bn), y de manera similar con su frontera: V(Sn – 1). Estos resultados nos permitirán posteriormente una propuesta sobre el número π, pero, específicamente al respecto de π½.
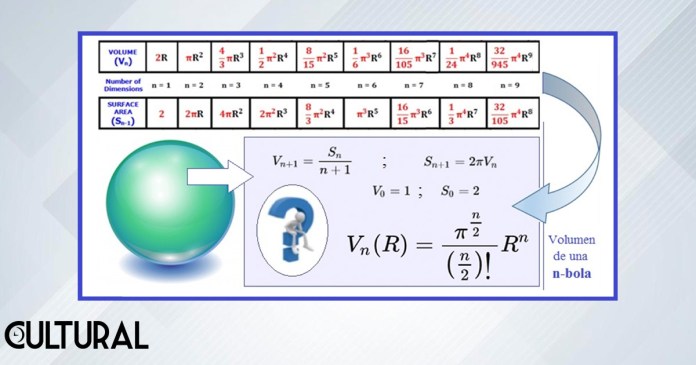
Así, para el cierre, reforzar la idea de las hipercajas como los objetos más simples en un espacio multidimensional, las cuales poseen un volumen que viene dado por el producto de las medidas de sus diferentes lados, o medidas componentes. Por otro lado, comprender que objetos no tan «planos» pueden ser definidos y precisados matemáticamente en un espacio de n dimensiones, como es el caso de la generalización de nuestra esfera en tres dimensiones, en cuyo caso hablamos de una n – esfera, o esfera n – dimensional. Puede darse una última ojeada a la fórmula para el cálculo del volumen de estas hiperesferas, en la cual, como hemos comentado, destaca el valor de π½, sobre el que esperamos retornar.
Fuente de imágenes ::
[ 2 + 5 + 6 + 7 + 8 ] Imágenes elaboradas por Vinicio Barrientos Carles
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: Wikipedia (prismatoid) + Wikipedia (prisma)
[ 3 ] Imagen editada por Vinicio Barrientos Carles :: O Baricentro da Mente
[ 4 ] Imagen editada por Vinicio Barrientos Carles :: Blog de Emilio Silvera V. + Concepto Definición + Wikipedia








