Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Las grandes mentes debaten sobre las ideas, las mentes promedio debaten sobre los eventos; las mentes pequeñas debaten solo sobre las personas.
Hyman G. Rickover
Hablamos de promedios todo el tiempo, con diferentes palabras, pero bajo una misma noción. Estamos familiarizados con la media aritmética, que la obtenemos, calculamos, sumando los valores en cuestión, y dividiendo, al final, este resultado entre el número de cantidades que hemos sumado. Por ejemplo, cuando procedemos a calcular el promedio de los valores 3, 10 y 17, aplicamos el algoritmo descrito, obteniendo 10 como respuesta. Entonces, afirmamos que el promedio de la colección de datos {3, 10, 17} es 10. Amerita comentar que sería más preciso expresar este hecho aseverando que la media aritmética de los tres números dados es 10, apuntando, por ejemplo: M (3, 10, 17) = 10.
Hemos escogido este ejemplo, en particular, para observar que cuando los datos se encuentran en progresión aritmética, este tipo de promedio se ubica al medio, es decir, en la posición central. De allí la denominación utilizada: media aritmética, o medio aritmético. Empero, se utiliza usualmente el femenino «media», pues se trata de una medida del centro, de la tendencia central, como suele llamársele a este estadístico de muestras.
Cabe explicar que se dice que la secuencia ordenada (3, 10, 17) está en progresión aritmética, porque los términos son equidistantes, es decir, cada uno se calcula sumando una cantidad fija al anterior, en este caso 7. Dicho en otras palabras, la diferencia entre dos elementos consecutivos de la secuencia es constante: 17 – 10 = 10 – 3 = 7. Si la secuencia se extendiera a más términos, obtendríamos la siguiente sucesión: 3, 10, 17, 24, 31…
Como estamos estableciendo, el promedio aritmético de una secuencia o sucesión aritmética se obtiene por inspección, sin hacer cálculos, solo observando qué valor se posiciona al medio, pues el promedio estará al centro. Así podemos saber que 10 es el promedio de 3, 10 y 17. Este concepto de colocarse al centro, estando ordenados los números, corresponde con la mediana, o valor mediano, otra medida estadística de la tendencia central en una distribución de datos.
Por otro lado, véase, que puedo obtener, rápidamente, la suma de 3, 10 y 17, que deberá ser 30, por ser tres veces 10. Esto es, las dos secuencias (3, 10, 17) y (10, 10, 10) tienen el mismo promedio aritmético y, por lo mismo, tendrán la misma suma. Así, se tiene que ambas secuencias tienen un promedio aritmético 10 y una suma de 30, lo que es evidente en la segunda secuencia (10, 10, 10). De esta forma, en general, puedo substituir cada dato por el promedio aritmético, que tendré un total, una suma, del mismo valor.
Una agradable anécdota vinculada con este hecho estadístico aritmético cuenta que, cuando el eximio matemático alemán Johann Carl Friedrich Gauss era un niño, en sus primeros años de escuela, solía abstraerse en «sus cosas», descuidando el seguimiento de las clases, como es frecuente en los infantes talentosos. No obstante, en cierta ocasión, el maestro decidió castigar a todos los chicos del aula, colocándoles como tarea obtener la suma de todos los enteros consecutivos entre el 1 y el 100. El joven Gauss se levantó al instante, entregando la respuesta al profesor, quien, sorprendido y anonadado, pudo verificar la sobresaliente elegancia y corrección del proceso.
Lo cierto es que Gauss destacó desde sus primeros años de vida, de lo cual su padre, un tenedor de libros, un contador, tuvo plena consciencia cuando el chico, de menos de cuatro años de edad, le corrigió los cálculos en unas sumas que estaba realizando. Por ello, no es extraño que desde muy joven haya descubierto esta propiedad del medio aritmético, que establece que la suma de una cantidad de números es siempre igual a n veces el promedio aritmético, en donde n representa la cantidad de datos. La gran ventaja es que estimar promedios, una cantidad intensiva, es mucho más fácil que estimar un total, una cantidad extensiva. Algo de esto hemos mencionado en «La densidad del agua».
El caso de la secuencia de números naturales, (1, 2, 3, … 99, 100), corresponde a una progresión aritmética, pues la diferencia entre un elemento y el siguiente es constante, siempre 1. Por ello, el prodigioso chico tomó los valores del centro, 50 y 51, procediendo a replicar su promedio 100 veces, esto es, multiplicando 50.5 x 100 = 5050. De manera similar a como es posible substituir la secuencia (3, 10, 17) por (10, 10, 10), en la cual la suma 30 es inmediata, el joven Gauss cambió la sucesión (1, 2, 3, … 99, 100) por esta otra, (50.5, 50.5, 50.5, … 50.5, 50.5), en la cual, nuevamente de forma instantánea, se obtiene una suma de 5050.
Empero, en forma lastimosa, la noción que hemos estado utilizando, la que usualmente aplicamos, refiere a un procedimiento operacional, no a un concepto en sí mismo, como suele suceder con la mayoría de conceptos aritméticos que manejamos, matemáticos en general, sean de índole geométrico o de algún otro tipo. Esto se debe a la mala orientación de los procesos educativos del sistema escolar, provenientes, no de ahora, sino heredados desde más de un siglo atrás. Sin embargo, al margen de estas falencias, por otro lado, podemos rescatar aspectos valiosos en el uso coloquial que damos a la palabra, que aportan positivamente a una pertinente noción de promedio, lo que nos indica que el concepto no se encuentra del todo perdido.
Esto lo podemos apreciar cuando utilizamos el término fuera del campo numérico, es decir, con objetos que no son números, sino de otra naturaleza o condición, como cuando hablamos, por ejemplo, de una persona promedio. Es decir, es bastante obvio que no podemos sumar personas, o dividirlas, porque no se trata de números o cantidades de algo. Así, al reflexionar, nos percatamos que la idea que manejamos de un «promedio», lo que la palabra significa, tiene que ver con «estar por el medio», esto es, al centro, que no asume extremos, sino que anda por la mitad de las posibles ocurrencias del fenómeno del que estamos hablando.
Hasta este momento hemos descrito la más conocida forma de encontrar un promedio de una serie de valores numéricos, de aspectos que derivan en datos cuantitativos. No obstante, de lo conocido y familiar que nos resulta la media aritmética, en esta oportunidad estaremos introduciendo otras formas de obtener un promedio, cuando se trata de valores numéricos, es decir, como hemos apuntado en lo previo, cuando cuantificamos un aspecto o variable de interés, la cual refiere a una dimensión en los objetos del universo de estudio. El titular responde a la denominación que la posteridad asignó a tres medidas de tendencia central, muy utilizadas por los antiguos griegos, a saber: la media aritmética, la media geométrica y la media armónica.
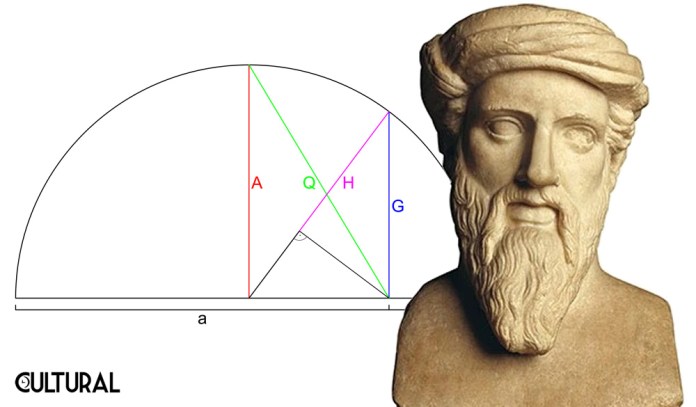
Se sabe que la escuela pitagórica conocía y utilizó ampliamente estos tres tipos de promedio, de los que pasaremos a ver su concepto, interpretación y posible aplicación. Lo primero que debe quedar claro es que todas estas son medidas del centro de un conjunto o distribución de datos, pero que responden a distintos criterios. En ciertos casos, solo una de estas medias podría ser considerada la correcta o más adecuada, y de allí la importancia de su conocimiento. En la imagen que sigue se aprecia una construcción que muestra la media geométrica h, de las dos cantidades p y q que se definen en cualquier triángulo rectángulo, cuando este se coloca sobre su hipotenusa.

Cercano a nuestro objetivo de esta oportunidad, el de presentar otras variedades de cálculo para el concepto de promedio, las correspondientes al titular, cabe citar el artículo «Prolegómenos a los promedios: aritmético y geométrico». En esa ocasión, explicábamos que, en la mayoría de los casos, existe una colección de objetos, de los que nos interesa el estudio o análisis de una determinada variable, resultante de algún tipo de medición. En cualquiera de las situaciones, la acción de promediar, es decir, de tomar promedios, busca una representación de la colectividad, efectuándose sobre los valores que la variable de interés asume en los objetos, pasando a hablar del «objeto promedio».
Es el caso de las personas, las cuales concebimos como objetos multidimensionales, es decir, explicadas mediante varias dimensiones o aspectos independientes. Empero, cuando hablamos del promedio, el contexto aclara y especifica a qué dimensión y a qué variables nos estamos refiriendo. Estas distinciones teóricas revisten una cierta importancia, para no incurrir en errores posteriores.
Coloquemos un ejemplo que ilustre lo expresado en el párrafo anterior. Al considerar una cierta tienda de abarrotes, es posible y frecuente hablar del consumidor promedio. Aquí el objeto medio será una persona, pero la variable que atañe, en este caso, es el gasto o consumo total que un cierto comprador en la tienda realiza, de manera tal que este consumidor promedio tendrá la propiedad de gastar en los posibles productos en venta una cantidad tal que viene a ser el promedio de todos los gastos registrados por la tienda. Queda claro que no hemos promediado las personas, sino únicamente un aspecto de ellas, léase: el gasto que realizan en la susodicha tienda de abarrotes.
El universo del discurso de los objetos en cuestión estará constituido por todas las personas que se acercan a la tienda y compran algún tipo de productos, algunas y algunos clientes pocos, mientras otras y otros muchos. Al tomar el promedio sobre todos los gastos, efectuados o estimados, tendremos el promedio de gastos y la persona correspondiente será el consumidor promedio. Lo que promediamos son los gastos, pero, a final de cuentas, hablamos de la «persona promedio», para referirnos a aquellos o aquellas que gastan un valor medio en los ciertos abarrotes. Existe una gran cantidad de ejemplos similares que ilustran el uso de esta terminología.
Pero regresando al asunto, cabe reparar en la premisa tácita que, cuando hablamos del cálculo de promedios, pensamos inevitablemente en la consabida media aritmética. Como pasamos ahora a ver, existen otro tipo de promedios, siendo estas otras variantes las pertinentes a utilizar en ciertas ocasiones, en vista de que se adecúan de mejor manera a la interpretación y la aplicación en esas situaciones. Primero, traigamos a la memoria a la media geométrica, presentada en los prolegómenos del enlace de más arriba. La razón para el término geométrico podría responder a varias posibles razones, en vista de que los pitagóricos, y los antiguos griegos en general, solían interpretar casi todas las entidades matemáticas de manera geométrica, incluyendo a la media aritmética.
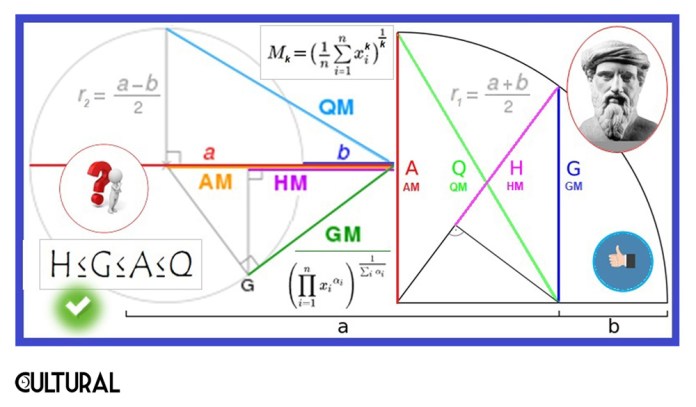
La imagen precedente explica, en parte, el sentido «geométrico», de la media geométrica (GM), además de que se incluyen los algoritmos usuales para el cálculo de las denominadas medias pitagóricas. Obsérvese la media armónica, simbolizada allí por HM. Sin embargo, enfoquémonos, por ahora, en la figura del triángulo. Se trata de un triángulo rectángulo cualquiera (escaleno), ubicado en la esquina superior izquierda. Se ha colocado sobre su hipotenusa, partiéndolo en dos, al trazarse la altura h. Queda una región amarilla, de base p, y una región roja, de base q. Como se aprecia visualmente, h es mayor que p, pero es menor que q. Esto significa que, si se ordenan de menor a mayor, obtendríamos la secuencia: p, h, q.
Lo anterior puede escribirse así: p ≤ h ≤ q. De hecho, siempre se tiene que p < h < q, a menos que p = q, en cuyo caso h también es igual a estas partes. Pues bien, resulta que h es la media geométrica entre p y q, y los griegos la calculaban, justamente, mediante este procedimiento, según puede apreciarse en la imagen subsiguiente. La demostración de que h resulta ser la media geométrica de p y q puede observarse en la parte baja de la imagen precedente, en donde se hace ver que h2 = pq, lo que garantiza el hecho.
Por otro lado, nótese que la demostración visual consiste en un arreglo de las regiones amarilla y roja, en un nuevo acondicionamiento del originalmente planteado, con la región verde que se genera, de dos maneras diferentes. La región verde, al ser el resto del total, al sustraer la región amarilla y la región roja, deberá ser equivalente. Una de las regiones verdes, la de la izquierda, es equivalente a h2, mientras la otra, la de la derecha, es igual a pq, de donde: h2 = pq.
No obstante, quizá la más probable causa para el uso del calificativo «geométrico» en este tipo de promedio sea similar al que ya hemos citado para el caso de la media aritmética. Recuérdese que la media aritmética se situaba al centro de una sucesión aritmética, y de allí la denominación. Vimos que en (3, 10, 17) la media es 10, que está al centro. De igual forma, en (1, 2, 3, 4, 5) la media aritmética, por inspección, será 3. Por ello, en el caso geométrico, deberemos considerar una sucesión o progresión geométrica, en la cual cada término se obtiene de multiplicar por un factor fijo, de manera que la razón entre cualquiera dos elementos consecutivos es constante.
El caso simple de la duplicación sostenida nos da un ejemplo: 1, 2, 4, 8, 16. Muchas y muchos hemos realizado esta situación de ir duplicando, de manera que el siguiente término siempre será el doble del anterior. Empero, podríamos aplicar otro factor, e iniciar con otro valor distinto de 1. Por ejemplo, si empezamos en 2 y aplicamos el factor 3, tendremos: 2, 6, 18… Pues bien, en la primera secuencia (1, 2, 4, 8, 16), decimos que la media geométrica es 4, mientras que en (2, 6, 18) decimos que es 6. Así, anotamos G (1, 2, 4, 8, 16) = 4 y G (2, 6, 18) = 6. Nótese que las medias aritméticas son distintas, puesto que M (1, 2, 4, 8, 16) = 31/5 = 6.2 y M (2, 6, 18) = 26/3 = 8.6+.
En otras palabras, como pasaremos a ver a continuación, la media geométrica debe ser utilizada cuando las observaciones o datos provienen de procesos de naturaleza multiplicativa, como sucede con los factores, tasas y todo lo referido a valores relativos, es decir, obtenidos mediante razón o comparación de valores netos. En la siguiente imagen, repetimos la forma de calcular la media geométrica, en un caso general, cuando los valores de la muestra de datos no se encuentran necesariamente en progresión geométrica. Por otro lado, se apunta el hecho ya anotado, que A ≥ G, en donde A simboliza la media aritmética de los datos en cuestión.
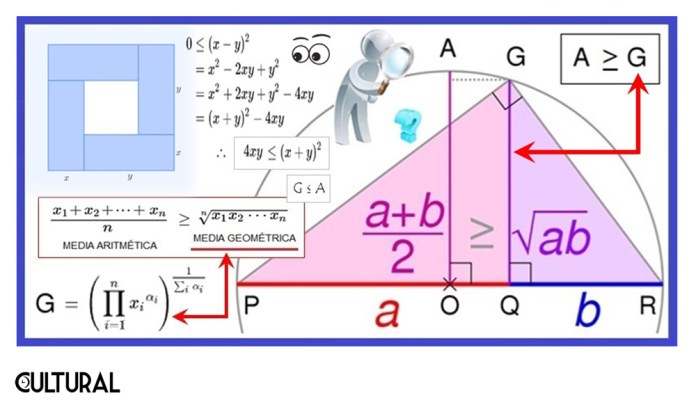
Como hemos anotado en lo previo, los antiguos griegos no solo conocían de esta forma de obtener promedios, sino obtuvieron demostraciones de las relaciones entre estas. En particular, el hecho que A ≥ G para el caso de dos números lo demostraban mediante la imagen mostrada en la derecha de la imagen previa, puesto que, dadas dos medidas (números) a y b, la construcción hace evidente que la media geométrica de a y b, G, la altura del triángulo rectángulo resultante, debe ser menor que la media aritmética correspondiente, A, que corresponde al radio de la circunferencia que tiene por diámetro la hipotenusa de tal triángulo. A la izquierda otra prueba visual de que G (x, y) ≤ A (x, y).
Hasta aquí hemos establecido que, al considerar una progresión geométrica, el centro será ocupado por una nueva medida de tendencia central: la media geométrica G. Esta secuencia geométrica, o exponencial, la obtenemos, la construimos, aplicando el mismo factor de crecimiento, o decrecimiento, a cada uno de los términos de la sucesión. En este sentido, uno o una podría pensar que, al tratarse de una secuencia obtenida por multiplicación, la media geométrica, G, sería mayor que A, la media aritmética. Sin embargo, en los ejemplos que hemos colocado ha quedado G más pequeña que A.
Este resultado es general, pues siempre se tendrá que A > G, siendo igual únicamente en el caso en que todos los datos son el mismo, en cuyo caso ambos tipos de promedio coincidirán, es decir, serán ambos el valor de la constante en cuestión, es decir: G (C, C, C, … , C) = A (C, C, C, … , C) = C, en donde G representa media geométrica, A representa media aritmética y la literal C refiere al valor constante de que estamos hablando. En este momento será conveniente ver un caso de aplicación de este concepto de sucesión geométrica y, por ende, de la media geométrica, asociada, como la forma «correcta» de tomar el promedio. Será deseable un ejemplo al que le veamos una utilidad evidente.
Hemos dicho que la sucesión geométrica se construye con multiplicación. Recordemos el tema de cobrar, o pagar, un interés, es decir, concerniente al cálculo de un determinado rédito por un préstamo que hemos realizado (perdón por recordar eso de las innombrables tarjetas de crédito). Pues bien, lo que se acuerda en este tipo de negocio es una cierta tasa, o porcentaje, de interés. Para facilidad en los cálculos numéricos, haremos un ejemplo con un número un tanto redondo, digamos, 10 % (por dicha, que esa no es la tasa usual en los créditos de las tales tarjetas).
Entonces, si habláramos de un interés simple, la secuencia en el tiempo de los montos adeudados sería así, suponiendo un capital inicial de 100: 100, 110, 120, 130, 140. Estamos considerando cinco momentos, esto es, cuatro períodos de tiempo. Es claro que la secuencia es aritmética y el monto medio adeudado es 120. Sin embargo, sabemos que un operador financiero no aplica este concepto del interés simple, puesto que carga el 10 % sobre cada nuevo monto, no sobre el capital inicial, por lo que se tratará de un interés compuesto. Es decir, al segundo período, no calcula el 10 % sobre 100, sino sobre los 110 que se adeudan. Así, la secuencia obtenida es geométrica, a saber: 100, 110, 121, 133.1, 146.41
La secuencia financiera de los montos obtenidos al aplicar el concepto del interés compuesto es geométrica, pues cada término se obtiene multiplicando el término anterior por un factor fijo. Si se analiza, en la secuencia de nuestro ejemplo el factor constante es 1.1, obtenido de 1 + 10 % = 1 + 0.1 = 1.1. El tiro es que el monto medio adeudado ya no es 120, sino 121, que está al centro de la sucesión de montos, es decir: G (100, 110, 121, 133.1, 146.41) = 121.
Como hemos dicho más arriba, la media geométrica debe calcularse cuando los datos se encuentran asociados a procesos de naturaleza multiplicativa, como es el caso tasas o de valores relativos, es decir, obtenidos mediante razón o comparación de valores netos. En la Wikipedia se lee un ejemplo de esta situación:
Una cadena de expendedores de gasolina el año pasado aumentó sus ingresos respecto al año anterior en 21 %; y han proyectado que este año van a llegar a un aumento de 28 % con respecto al año pasado. ¿Cuánto es el promedio anual del aumento porcentual? Definitivamente no es ½ (21 % + 28 %) = 24.5%.
Lo hemos citado pues es frecuente encontrar este error de calcular la media aritmética de las dos tasas de crecimiento, que arroja este resultado de 24.5 %. La respuesta correcta de la tasa media viene dada por la media geométrica de los factores de cambio. El asunto es que no se trata del caso de una sucesión geométrica, sino de una situación general. En breve, el procedimiento es el de multiplicar los valores de los que se trata, sacando al final una raíz n-ésima, siendo n el número total de datos que hemos multiplicado. En el caso de n = 2, de dos valores, a y b, haremos la operación (ab)½, que es la raíz cuadrada del producto ab.
De esta manera, en el caso citado de las dos tasas de crecimiento, 21 % y 28 %, deberemos proceder geométricamente, esto es, de forma multiplicativa. A su vez, el dato a promediar no es la tasa en sí misma, sino los factores de cambio, que son, para cada año, 1.21 y 1.28. De esta forma, calculamos G (1.21, 1.28) = (1.21 x 1.28) ½ ≃ 1.24451, de donde la tasa promedio (geométrica) será de 24. 45 % aproximadamente. Nótese que el cálculo A (1.21, 1.28) = 1.245 arroja una tasa promedio (aritmética) de 24.5 %, que sobreestima la verdadera tasa media. Nuevamente, G < A.
Por otro lado, quizá regresar al caso del consumidor medio, en el cual la variable a promediar es el gasto en la tienda de abarrotes. Esto es importante, pues siempre es importante identificar los objetos de estudio y las variables a promediar. Por ejemplo, si se tratara de personas en un grupo de estudio de casos, podríamos considerar varias dimensiones, por ejemplo: edad, estatura, peso y frecuencia del padecimiento. La persona media sería aquella que en cada dimensión tiene el valor medio en la población, pudiendo esta persona no existir en la muestra, sino ser un objeto del cual no hay instancia empírica de observación, como cuando se dice que el número medio de hijos por familia es de 2.7
Con los ejemplos planteados, estamos dejando en claro que el concepto de tomar un promedio es más general que el de calcular una media aritmética. Retornando al caso de las personas promedio, podríamos considerar un aspecto cualitativo, nominal, no fácilmente cuantificable, digamos, la belleza. Vemos que, aunque, no hay valores, podemos aplicar un criterio de orden en los objetos, utilizando esta ordinalización para obtener un promedio. En otros casos ni el orden será posible. Por ello existen otros promedios, como la mediana y la moda, que nos sirven cuando no podemos calcular una media, cuando no existen valores numéricos, cuantificaciones, de la variable de interés.
Las medias que hemos mencionado hasta ahora operan y funcionan con variables numéricas, habiendo sido estudiadas por la escuela de Pitágoras de Samos, y por ello recibieron de la posteridad esa denominación. Sin embargo, existen otras medias importantes que tienen su particular ámbito de acción y de validez, como es el caso de la media cuadrática, importante en el cálculo de desviaciones, sesgos y errores de medición. A continuación, una imagen que muestra cómo dados dos valores a y b, es posible calcular, mediante trazo de regla y compás, las medias mencionadas.
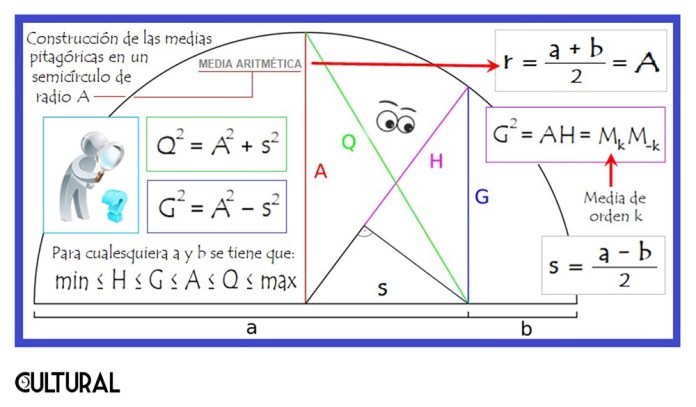
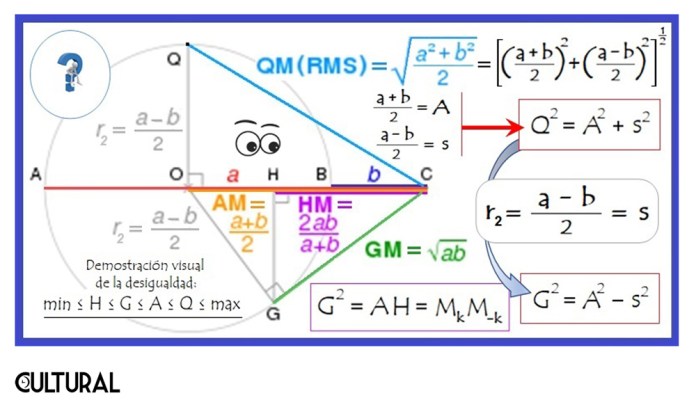
En la imagen precedente se observa la media aritmética A, como el radio del semicírculo, en color rojo, y la media geométrica G, en color azul. También aparecen la media armónica H, en color violeta, y la media cuadrática Q, en color verde. Se observa y se anota la desigualdad que siempre se da entre estas medidas, no solo para el caso de dos datos, a y b, sino con cualquier cantidad de números a promediar, a saber: m ≤ H ≤ G ≤ A ≤ Q ≤ M, en donde m es el mínimo valor asumido y M es el máximo, respectivamente.
Finalmente, la siguiente última imagen proporciona otra forma de graficar estas cuatro medias mencionadas, las tres pitagóricas y la media cuadrática, sobre la cual podremos regresar en futura oportunidad. También nos quedamos debiendo otros ejemplos que nos aclaren de mejor forma cuando usar un promedio y cuando usar otro. En miras a no alargarnos demasiado, dejamos en la espera estos casos ilustrativos, en la expectativa de haber despertado el natural y suficiente interés por el tema. Como hemos dejado ver entre líneas, en esta breve introducción, el concepto y la acción de promediar es fundamental para comprender la información que nos llega, para interpretar correctamente los datos y la realidad.
Sumariando, hemos mencionado la anécdota del joven Gauss, que muestra cómo a través de un valor promedio, sea del tipo que sea, podemos pasar a estimar un total o la generalidad de la colectividad. En general, una variable de tipo intensivo representa localmente a un objeto de estudio, y funciona como un buen y eficiente estimador para otras magnitudes extensivas asociadas. Esto se debe a que las magnitudes intensivas son siempre promedios pesados, ponderados, en un todo, que es una mezcla, extensiva, de todas las partes que componen ese todo, trátese de una población humana, trátese de un objeto macroscópico termodinámico, o trátese de un cuerpo con cierta energía total. Esta distinción entre localidad y globalidad tiene relevancia en la Topología, de la que hemos escrito recientemente.
Fuente de imágenes ::
[ 1 + 4 + 5 ] Imágenes editadas por vbc :: https://es.wikipedia.org/wiki/Media_geom%C3%A9trica + https://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means
[ 2 + 3 ] Imágenes tomadas de gAZeta, editadas por vbc :: https://www.gazeta.gt/prolegomenos-a-los-promedios-aritmetico-y-geometrico-iii/