Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Dondequiera que haya un número está la belleza.
Felix Christian Klein
Nuestra frase motivante está tomada de las varias atribuídas a Felix Klein, un importante matemático alemán de quien, en la Wikipedia, puede leerse lo siguiente: «demostró que las geometrías métricas, euclidianas o no euclidianas, constituyen casos particulares de la geometría proyectiva [presentando] , en 1871, una notable clasificación de la geometría, en el denominado programa de Erlangen». Y no es para menos citarle, pues con matemáticos de la talla y profundidad de Klein, se terminó de consolidar la nueva Matemática, matizándola como la conocemos y entendemos al día de hoy.
Esta consolidación, que comentamos se refiere a su definición como disciplina abstracta, totalmente independiente de las concreciones que posee el mundo empírico sensorial, terminaría por dejar de lado las realidades tangibles, apegándose únicamente a las necesidades que la lógica y las axiomáticas particulares imponen. Un claro ejemplo de esta autonomía, emergió justamente de las geometrías no euclideanas, que parecían no intuitivas, así como sucede con otras estructuras matemáticas, en donde esta independencia de la realidad sensible se haría paulatinamente evidente. Así, por ejemplo, en la clasificación realizada por Klein, el concepto algebraico de grupo pasaría a desempeñar un papel fundamental, en vista que cada tipo de geometría sería descrita perfectamente como el estudio del grupo de transformaciones propias.

Sin embargo, a pesar de las diferentes ramas incluidas actualmente en la disciplina matemática, que ha crecido enormemente en el último siglo, multiplicándose en un factor superior a 20, resulta que la mayoría de las personas siguen concibiendo a la Matemática como aquella ciencia dedicada al estudio de los números y sus propiedades. Aunque esta conceptualización no es acertada, también es cierto que la numeración y los secretos que encierran los distintos campos numéricos representan el primer estímulo matemático a los que el ser humano primitivo debió enfrentarse, como pudimos comentar en «Quetta y ronna al SI», al hablar sobre el conteo y la medición como parte medular de las primeras abstracciones.
También conviene acotar que, en estos contextos coloquiales, cuando hablamos de «números», nos estamos refiriendo al conjunto de los números naturales: ℕ = { 0, 1, 2, 3, … }. Como sabemos, se trata de un conjunto infinito, en donde sus elementos establecen una sucesión que nunca termina, por decirlo en términos intuitivos. Esta infinitud fue la principal razón por la cual los números tuvieron que tener un tratamiento puramente lógico y formal. Así, por caso, cualquier demostración que haga ver que los números primos, irreducibles, los que no admiten una partición exacta, son infinitos en cantidad, viene a ser una obra maestra del raciocinio puro.
En esta ocasión, abordando el tema de las propiedades numéricas, queremos colocar sobre la mesa una interesante propiedad del número 2023, correspondiente al año que estamos iniciando. Se ha vuelto una tradición, medianamente popular, el compartir propiedades del número del año que empieza, similar al planteamiento de renovadas metas motivantes. No obstante, antes de conversar sobre ello, consideramos oportuno enfatizar esto de que la Matemática es una colección de sistemas formales, no exclusivamente numéricos, sino, en general, relativos a todo tipo de estructuras lógico formales, que suelen asumir ciertas significancias, al momento de ser aplicadas en la ciencia o en otras áreas de la existencia. Por ello hemos citado a la Geometría y la forma como ahora se le concibe.
Por otro lado, si para el lego lo matemático es todo lo relacionado con los números (ya hemos dicho que esto es impreciso y no del todo correcto), también sucede que, para el matemático profesional, hablar de números a un público general le resulta un tanto más cómodo, por expresarlo de alguna manera, pues el material, dada la educación que hemos recibido, suele resultar familiar a cualquiera con quien conversemos. En complemento, tratamos con números en todo momento, por lo que más de algo nos ha resultado interesante o fácil de comprender. Aquí es vital que distingamos entre dos situaciones, o entidades, distintas, a propósito de nuestra finalidad en torno de una singular propiedad del 2023.

En efecto, al anotar los guarismos (símbolos) «2023» es importantísimo diferenciar entre el número representado y el numeral que lo representa. Para evidenciar esta distinción, veamos un símil, partiendo de un campo del discurso más general. Todas y todos sabemos que las palabras denotan conceptos, y algunas en particular hacen referencia a objetos. Por ejemplo, en castellano, la palabra «mesa» hace referencia a una mesa, que todos aprendemos de infantes a identificar y reconocer. La mesa es un objeto, mientras que «mesa» es la forma en la que representamos tal objeto en el lenguaje en cuestión. La palabra puede tener ciertas propiedades que no se refieren al objeto, sino a la palabra, como estamos especificando.
Visibilizando lo que hemos escrito, nótese que «mesa» es una palabra grave que tiene cuatro letras, propiedades que para nada están vinculadas con la mesa a la que podríamos estar haciendo referencia. Nótese que estas propiedades están conectadas al lenguaje que estamos usando, porque, por ejemplo, en idioma inglés, la palabra correspondiente a mesa tiene cinco letras (table) y una fonética distinta. Lo importante acá es distinguir entre la palabra y el concepto, u objeto, al que hace referencia. Lo mismo sucede con los números, que al igual que los conceptos, en general, pueden ser expresados en varios idiomas, o sistemas de numeración.
El sistema de representación numérica que universalmente usamos en el mundo cotidiano es el sistema de numeración decimal, y estamos tan familiarizados con él, que usualmente confundimos el número con su representación, que se denomina numeral. Por ejemplo, al pensar en el número doce, en una docena, viene rápidamente a nuestra mente la secuencia «12». Sin embargo, esta secuencia, la palabra «12», no es, ciertamente, el número doce (12), sino que es la forma en que escribimos este número. El objeto es el número 12, y la palabra, en el sistema decimal, es «12».
De esta guisa, «12» es el numeral que representa al número que tiene 1 unidad de primer orden y 2 unidades básicas. En base diez (10), la unidad de primer orden vale precisamente 10, de forma que «12» representa la suma de una decena con dos unidades básicas, lo que nos da una docena, esto es: 12 = 10 + 2. Sin embargo, en base cinco (5), la unidad de primer orden vale 5, por lo que «12» viene a representar la suma de una unidad de primer orden (5) con dos unidades básicas, lo que da por resultado siete: 7 = 1 x 5 + 2 x 1. Esto lo escribimos así: 12diez = 1 x 10 + 2 x 1 = 12; 12cinco = 1 x 5 + 2 x 1 = 7.
De lo anterior, la palabra «12» vale 12 en el sistema decimal, mientras que en el sistema base cinco vale 7. Conviene leer «12» como «uno_dos» cuando no se está claro cual es la base del sistema de numeración. Así, un determinado numeral, como el caso de «12», valdrá distinto según sea la base del sistema en el que se escribe. De manera inversa, si alguien desea escribir el número 12, este número tendrá diferente numeral en cada sistema. Doce se escribe «12» en decimal, «22» en sistema de base cinco, y «1100» en sistema binario, o de base dos, que es el utilizado en los ordenadores electrónicos.
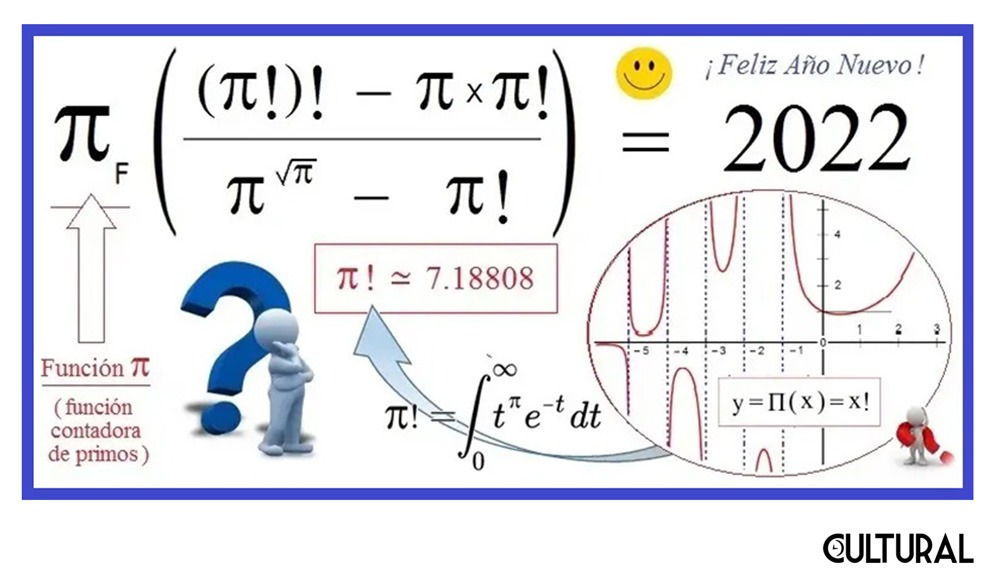
Esta acotación viene al caso de que existen propiedades que son inherentes al número, mientras otras hacen alusión al numeral, usualmente el del sistema decimal. Las propiedades inherentes a los números son, de manera esencial, más fundamentales que las relativas a los distintos numerales que lo representan. Estas segundas vienen a ser curiosidades o diversión, en un área conocida como matemáticas recreativas. Como ahora estamos trayendo el 2023 a la palestra, resultaba medular distinguir entre el 2023 y su numeral decimal, el «2023». A continuación, una copia de la imagen del año pasado, tomada del artículo «Factores y factoriales para un nuevo año», con un curioso cálculo, basado en el número π, que arroja al final el número 2022.
Antes de pasar a nuestro esperado 2023, amerita ilustrar un poco más la distinción entre el número 2023 y el numeral «2023». Una de las propiedades esenciales de los números naturales (los elementos en ℕ) están relacionadas con su factorización, esto es, con los divisores primos que posee. En efecto, el teorema fundamental de la aritmética, que establece que todo número natural tiene una factorización única en números primos (o irreducibles), sin tomar en cuenta el orden de los factores, permite describir muchas de las propiedades esenciales de un número cualquiera. De esto que, lo primero que podemos hacer con un número dado, es encontrar su factorización en números primos.
Esta factorización refiere al número en sí, y no a la forma en que se represente el número en cuestión. Así, por ejemplo, 7 es un número primo, esto es, que solo tiene un factor, se escriba como se escriba, mientras que 6 tiene dos factores, 2 y 3, nuevamente, sin importar en el sistema que se utilice para representarlo. Por otro lado, el número 6 es perfecto, pues es la suma exacta de sus divisores (factores) propios: 6 = 1 + 2 + 3. Si regresamos al número 12 antes citado, su factorización nos queda así: 12 = 22 x 31. O sea que 12 tiene, como factores primos, dos factores 2 y un factor 3.
Nótese que 12 es el único número con esta factorización, y viceversa. De hecho, la representación universal para cualquier número natural proviene de su factorización única en números primos. Si otros seres inteligentes en el universo procedieran a representar los números naturales, sabemos que sería mediante su descomposición fundamental en números primos. En una página como en este enlace puede consultarse la factorización de un número natural cualquiera. En anterior artículo hablamos de la clasificación de Nicómaco, pero aprovechamos el momento para indicar que una clasificación más fundamental viene dada por la cantidad de factores primos que posee un determinado número.
La Aritmética, también conocida como Teoría de números, es la rama de la Matemática que estudia los números naturales. Carl Friedrich Gauss decia: «la Matemática es la más sublime de todas las ciencias, y la Aritmética es la reina de todas las matemáticas». En efecto, se ha dicho que las interrogantes más profundas provienen de la Teoría de números, en la que muchos y muchas se han sumergido en profundidades inimaginables. Aún así, los problemas pueden ser entendidos por quienes no poseen mayores estudios, como es el caso del último teorema de Fermat, conjeturado en 1637. A pesar de comprender lo que la conjetura expresaba, no fue sino hasta 1995 que Andrew Wiles logró demostrarla.
Regresando a la distinción entre el número y los numerales, coloquemos un ejemplo más. En virtud del teorema de la factorización única, sabemos que un número puede tener un determinado primo en su factorización, o no tenerlo. Si aparece el 2, es decir, si el 2 es un factor del número, decimos que es par, o divisible por 2. Un número dado es par, o no lo es, en cuyo caso decimos que es impar. De similar forma, el número en cuestión podría tener el factor 3, en cuyo caso será un múltiplo de 3. Nuevamente, o es múltiplo de 3, o no lo es.
Un tema clásico de la aritmética elemental es el de los caracteres de divisibilidad, es decir, los algoritmos de reconocimiento para saber cuándo un número dado es divisible por cierto número primo en particular. En la base diez, como 10 tiene por factores el 2 y el 5, será muy fácil reconocer cuándo un número dado escrito en el sistema decimal de numeración es divisible por 2 o por 5. Sabemos que basta con ver su cifra terminal. Son pares aquellos números cuyos numerales terminen en cifra par, y son múltiplos de cinco los que terminan en un dígito múltiplo de cinco, es decir, cuando terminan en 0 o en 5. Sin embargo, esta caracterización aplica solo al numeral decimal.
Es decir, ser par o no serlo corresponde al número, pero el reconocimiento puede realizarse fácilmente si lo escribimos en base diez. La regla de terminar en 0 y ser múltiplo de 5 no aplica, en general, en otros sistemas de numeración. Por ejemplo, en el sistema binario, el numeral puede terminar en 0 y no ser múltiplo de 5, o a la inversa. Igual con los múltiplos de 3, para los que en sistema decimal sumamos sus cifras. En síntesis, poseer un factor es una característica del número, pero identificar esta característica se encuentra vinculada al numeral. En el caso del 2023, podemos ver que no es múltiplo de 2, ni de 5, puesto que termina en 3.
La sospecha inmediata es que 2023 podría ser un número primo. Para despejar la duda, deberemos checar exhaustivamente la lista de números primos: P = { 2, 3, 5, 7, 11, 13, 17, … }, para ver si alguno es divisor. Para el 3, sumamos las cifras de «2023», que nos da 7, por lo que no es un múltiplo de 3. Antes, la factorización en primos requería de cálculos y diversos algoritmos. Ahora, sin embargo, es muy fácil acudir a una página web, como la que hemos apuntado arriba, encontrando que, en efecto, 2023 no es un número primo, sino que tiene tres factores, con únicamente dos primos, a saber: 7 y 17. Específicamente, posee un 7 y dos 17, esto es: 2023 = 71 x 172.
La clasificación que mencionamos refiere a la cantidad de números primos que posee una factorización dada. Así, podríamos llamar de primer tipo, o primarios, a aquellos números que poseen únicamente un número primo p, siendo de la forma pn. Los números de segundo tipo, o secundarios, pasarían a ser aquellos que su descomposición en factores primos contiene exactamente dos primos, p y q, siendo, por tanto, de la forma pnqm. Este es el caso del 2023, pues su descomposición usa dos primos únicamente: el 7 y el 17. La factorización 71 x 172 corresponde a la forma pnqm.
La singularidad, publicada por la Sociedad Matemática Americana, AMS (por su siglas en inglés, American Mathematical Society), refiere al hecho de que, cabalmente, la suma de las cifras del numeral es 7, mientras la suma de los cuadrados del numeral es 17, de manera que el 2023 es un número que cumple con la propiedad mostrada en la imagen siguiente. Vemos que esta propiedad vincula la factorización con una característica asociada al numeral decimal «2023». Una primera pregunta matemática será si esto es frecuente, o, en dado caso, lo cual sería altamente deseable, se trata de una característica que únicamente se cumple en el 2023. Verifíquese en la imagen lo que la propiedad establece.

Aunque estas preguntas relacionadas con las curiosidades de la matemática recreativa no son en sí mismas medulares en la investigación matemática, puede suceder que una prueba de unicidad, o de casos únicos, conlleve algunos problemas no elementales que a más de alguien pudiera interesar. Es el caso del denominado número de Sheldon, el 73, que surgió en uno de los programas de la serie televisiva Big Bang Theory, en donde se afirmó la peculiaridad de este número, que uno de los protagonistas esgrime como su favorito. Al igual que con nuestro 2023, verificar que los números cumplen lo que se dice es la parte fácil, o evidente, del problema.
No obstante, una prueba, o demostración, de que lo que se afirma se cumple únicamente en el caso citad, representa un nivel de problema que está muy por encima de la verificación de lo que se dice. En el caso de la demostración para lo que se dijo en el popular programa, derivó en años de investigación por parte de unos matemáticos, quienes se propusieron, a título personal, llevar a cabo la implícita demostración de que lo afirmado ocurría únicamente para el número 73. Será motivo de tratar posteriormente este singular ejemplo, y dejamos como inquietud de la comunidad matemática el estudio del caso de nuestro 2023.
Para el cierre, cabe subrayar que algunas peculiaridades numéricas recurren al numeral, como en el caso de nuestro 2023, o del fabuloso 153, del que escribimos el año pasado. Empero, algunas otras atañen al número exclusivamente, como es el caso de que 23 es primo, mientras que 2023 no lo es, o de que el 2022 es un número semiperfecto, en los cuales el numeral, o sistema de representación utilizado, viene a ser inmaterial y sin ninguna incidencia. Hemos insistido que, matemáticamente, este segundo tipo de propiedades resultan más esenciales.
Esperamos que el lector y lectora recurran a la página que hemos traido a colación, o a otras similares, sea para curiosear o divertirse un poco con el asunto de las propiedades numéricas. Después de todo, se encuentran cosas sorprendentes que no dejan de ser divertidas e interesantes. Por otro lado, para provocar la reflexión sobre lo que hemos planteado al inicio, sin alejarnos de la diversión que nos ha motivado a escribir esta publicación, deseo copiar del apartado «Belleza matemática», de la Wikipedia, lo siguiente:
Galileo Galilei dijo alguna vez: «Las matemáticas son el lenguaje en el que Dios escribió el universo», una afirmación que (aparte del implícito teísmo) es consistente con las bases matemáticas de toda la física moderna. El matemático húngaro Paul Erdös, aun siendo ateo, habló de un libro imaginario, en el que Dios había escrito las demostraciones matemáticas más bellas. Cuando Erdos quería expresar una particular apreciación a una demostración, solía exclamar: «¡Ésta es del libro!». Este punto de vista expresa la idea de que las matemáticas, como las verdaderas leyes en las que se basa la construcción de nuestro universo, son el candidato en el que se personifica Dios en diferentes religiones místicas.
Este brillante e icónico matemático, Erdös, sobre la belleza de los números, expresaba:
¿Por qué son bellos los números? Es como preguntar por qué es bella la novena sinfonía de Beethoven. Si no ves por qué, nadie te lo puede decir. Yo sé que los números son bellos. Si no lo son, entonces nada lo es.
Fuente de imágenes ::
[ 1 + 3 ] Imágenes elaboradas por Vinicio Barrientos Carles
[ 2 ] Imagen tomada de gAZeta, elaborada por Vinicio Barrientos Carles :: https://www.gazeta.gt/factores-y-factoriales-para-un-nuevo-ano/








