Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
El viaje en el tiempo ofende nuestro sentido de causa y efecto, pero tal vez el universo no insiste en la causa y el efecto. Edward M. Lerner
La palabra paradoja proviene del latín paradoxa, que a su vez deriva de las raíces griegas παρά (para) y δόξα (doxa), por lo que literalmente se traduce como contrario a la opinión general. De manera más acuciosa, se interpreta como una antilogía, o lo que es equivalente, como una idea o relación que lleva a una cierta contradicción, bajo las premisas y procedimientos de la lógica subyacente. Esto conlleva a una serie de situaciones que entran en conflicto, directa o indirectamente, con los postulados mínimos para la consistencia lógica en una determinada estructura, la cual se asume como válida en el discurso en cuestión.
Recientemente, en el artículo «El entrelazamiento y otros asuntos cuánticos», mencionamos la paradoja EPR (Einstein-Podolsky-Rosen), un argumento basado en el pensamiento del paradigma de la física clásica, con el que se pretendía echar por tierra la validez de la mecánica cuántica. Las paradojas, en su mayoría, demarcan de mejor forma las fronteras que deben considerarse en las estructuras teóricas y en los sistemas lógicos formales, cimientos ambos sobre los que descansan la validez misma de las teorías. Así, permiten demostrar la existencia de ciertos límites teóricos que antes del aparecimiento de la paradoja no se estaban tomando en cuenta. El ejemplo citado ilustra muy bien esta particularidad.
Las paradojas pueden ser clasificadas de varias maneras, y se encuentran documentadas desde tiempos muy remotos, originando debates durante muchos siglos, como es el caso de las paradojas de Zenón, relativas al infinito y el movimiento. La mayoría son resueltas mediante acotaciones en el uso del lenguaje, o bien definiendo con mayor precisión los esqueletos lógicos sobre los que descansa el discurso. Sin embargo, otras paradojas asumen la forma de contradicciones irresolubles, aporías, del griego ἀπορία, que significa «dificultad para dar el paso». Las aporías suelen hacer referencia a incompatibilidades lógicas esenciales, de índole especulativa, que, vinculadas con la realidad, parecieran no tener solución posible.
A pesar de la diversidad de paradojas, podríamos aventurarnos a aseverar que las que mayor impacto provocan en el sentido común son las que sostienen una relación con el mundo físico en el que nos desenvolvemos, puesto que atentan contra un postulado básico, que el universo es inteligible y racionalmente explicable. No podríamos estar tranquilos si descubriéramos que existimos en un mundo inconsistente, en el sentido lógico, o contradictorio, en cualquier otro sentido. Por ello las paradojas contienen elementos que desvelan fallas en las teorías, las cuales son ampliadas o corregidas en función de las paradójicas objeciones planteadas.
De similar forma, las aporías que en su momento se concibieron como fundamentales, han ido siendo superadas con desarrollos teóricos ad hoc, que han subsistido de mejor forma los embates de los siglos. Es el caso de una gran cantidad de paradojas matemáticas o lógicas, que ameritará abordar en posterior oportunidad. Nuevamente, las aporías relativas a la naturaleza o el cosmos son las que demoran más tiempo en ser superadas.
Es el caso de la búsqueda del arché (arjé) en el problema de la physis, que llevó del monismo al pluralismo, en la Liga jónica, y de las posiciones de filósofos como Anaxágoras, que concibiendo a la materia como extensa, procedían a subdividirla ad infinitum. De esto los atomistas Leucipo y Demócrito concluirá en la existencia de los indivisibles (ἄτομον), precuela rudimentaria de la física cuántica de la actualidad, que supera la noción de extensión, un estar ahí (determinista), por la pura posibilidad de estar ahí, de naturaleza radicalmente probabilista. Otro tipo de paradojas se originarán, como las relativas a la decoherencia cuántica y el problema de la medida, presentes en el gato de Schrödinger.
Para introducirnos en el fascinante mundo de las paradojas, estamos recurriendo a una no tan conocida. William Newcomb fue un físico teórico norteamericano que trabajó en el Laboratorio Lawrence Livermore. No sabríamos de él de no ser por la paradoja que lleva su nombre, ideada a inicios de los años sesenta. Tampoco la paradoja se hubiera popularizado de no ser por la difusión que el filósofo estadounidense, Robert Nozick, le dio en 1969, mediante su artículo Newcomb’s problem and two principles of choice (El problema de Newcomb y dos principios para la escogencia).

Aunque los intereses de Nozick, en aquel entonces profesor en la Universidad de Harvard, giraban en torno del libre albedrío y los problemas relativos a la toma de decisiones en el ámbito sociopolítico, la paradoja fue divulgada ampliamente entre filósofos, científicos y otra cantidad de especialistas. Fue publicada en la edición de marzo de 1973 de la revista Scientific American, en la prestigiosa sección Mathematical Games a cargo del gran divulgador de matemáticas Martin Gardner.
La paradoja plantea un acertijo lógico, un experimento mental, entre tú y una contraparte. Como protagonista, deberás decidir entre dos opciones, con diferentes beneficios cada una. Como es lógico, tú perseguirás obtener las mejores utilidades. Existen varias versiones del planteamiento, y nos estamos inclinando aquí por la que pensamos y esperamos sea más fácil de entender. Lo inquietante es la problemática que se abre en cualquiera de las variantes. Imaginemos, primero, que los beneficios de las dos opciones se miden por el dinero en efectivo que obtienes.
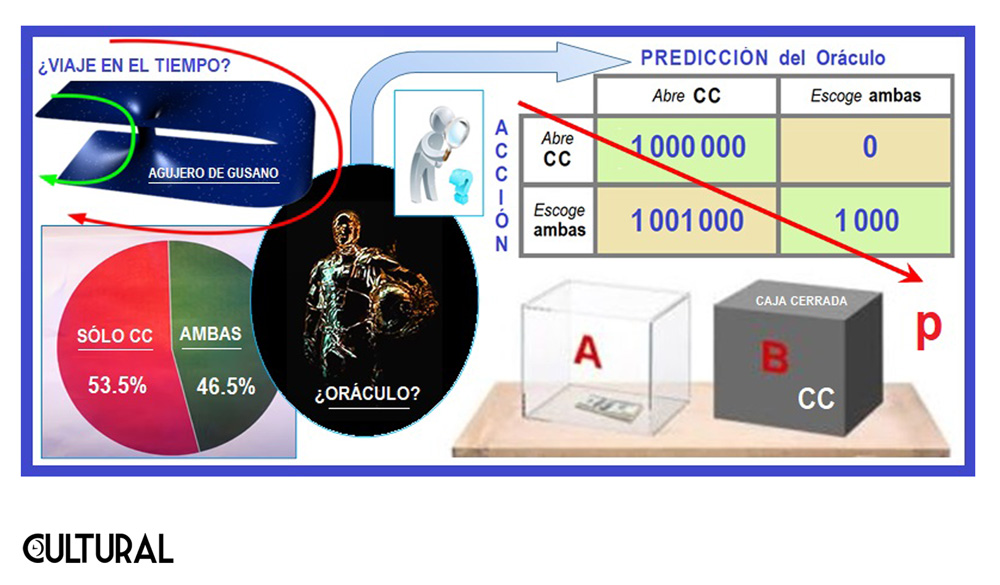
La situación es sencilla: tienes dos cajas al frente, una que es transparente y muestra Q 1,000 en efectivo en su interior, y otra que, es opaca, está cerrada y sabes que pudiera contener dinero. La caja cerrada (CC) podría no tener nada de dinero, esto es Q 0. Las dos opciones en el juego son: (a) tomas únicamente la caja cerrada (b) tomas ambas cajas. ¡No puede ser tan simple! exclamará para sus adentros quien nos lee. ¡¿Y qué de paradójico o especial tiene esta situación?!
Cualquiera dirá, «me inclino por la opción (b), tomo ambas cajas y me voy con los Q 1,000 de la caja primera y, como extra, me quedaría con el contenido de la enigmática caja cerrada CC». Estarías absolutamente en lo correcto. ¡No habría nada más que decir! No obstante, aún no te comparto quién es tu contraparte en el juego. Ante muchas versiones, todas poseen una característica en común: tu contraparte sabe de antemano lo que tú vas a escoger. En todas las opciones enlistadas luego, tu contraparte sabe, sin posibilidad de fallo, lo que tu elegirás, esto es, sabe si escogerás únicamente la caja cerrada (CC), o si optarás por llevarte ambas.
Y para prenderle fuego a la mecha, antes de continuar con los detalles, te comento la otra situación que despertará las primeras dudas al respecto. Resulta que tu contraparte, que sabe lo que decidirás en el juego, realiza con antelación una de las siguientes acciones: (a) si decidirás escoger únicamente la caja cerrada (CC), depositará en ella Q 11000,000; (b) si te inclinarás por llevarte ambas cajas, dejará la caja cerrada (CC) vacía, esto es, con Q 0. Haciendo una pausa con la lectura, tómate un tiempo, y piensa: ¿qué escogerías tú?… ¿solo CC o ambas cajas?
Revisando el planteamiento, será bueno saber con quién te estás enfrentando en tan extraño juego, esto es, que estás en libertad de colocar como adversario con quién te sientas más a gusto jugando. Hay quienes hablan de un ser supremo, omnisciente, o de un ser superior, tipo demonio, tipo ángel o tipo genio. Hay quienes prefieren pensar en una inteligencia cósmica o en un ser extraterrestre, venido de otra galaxia u otro universo. Hay quienes optan por hablar de un mago o un adivino, cuyo oráculo es infalible. Otros se imaginan un superordenador hiperdesarrollado que, después de conocerte lo suficiente, sabe con total certeza qué decidirás en todo momento.
Por último, una opción muy a la usanza de la ciencia ficción del cine y la TV, en la que te imaginas como contraparte a un ser humano común y corriente, pero proveniente del futuro, de manera que ya ha acontecido el encuentro y por lo tanto sabe que fue lo que escogiste, o, mejor dicho, lo que ahora estás por escoger. El objeto de estas opciones, distintas, pero equivalentes, es imaginar que tienes como contraparte a alguien que, con total y absoluta certeza, sabe lo que estás por hacer.
Lo inquietante de la paradoja, por lo que llama más la atención, es que, como bien señaló Nozick en su artículo de 1969:
Casi todo el mundo está perfectamente claro y le resulta bastante obvio lo que se debe hacer. [Curiosamente] la dificultad estriba en que las personas parecen dividirse casi de manera uniforme ante el problema, con un gran número de personas que piensan que la otra mitad, quienes deciden de manera opuesta, están, simplemente, haciéndola de tontos.
De hecho, el problema sigue dividiendo a los filósofos de hoy en día, y la polarización observada es lo que, al pensador, interesado en sociopolítica, le llamó poderosamente la atención. Específicamente, en aquel entonces, cuando el académico hizo su publicación, el 53.5 % se inclinaron por la opción (a), de escoger únicamente la caja cerrada, mientras que el 46.5% se inclinaron por la opción (b), de quedarse con ambas cajas.
La paradoja de Newcomb es, sin duda, una de las paradojas más enigmáticas e interesantes. Vinculada fuertemente con la ciencia ficción y las distintas situaciones que en más de una producción cinematográfica nos han hecho pensar, ha implicado el posicionamiento de los científicos más notables. Por ello el epígrafe del novelista estadounidense Edward M. Lerner viene como anillo al dedo. El escritor de ciencia ficción y suspenso tecnológico sabe perfectamente que los viajes en el tiempo, además de populares y atractivos, generan una serie de conflictos, que a muchos y muchas han procurado sesudas reflexiones.
Veamos más detenidamente en qué consiste el problema, o, dicho de otra manera, defendamos a quienes se posicionan en una u otra opción. Primero, quienes escogen llevarse únicamente CC suelen argumentar: puesto que mi contraparte sabe lo que haré, al tomar la caja cerrada habrá colocado en ella: Q 11000,000. Sería verdaderamente tonto llevarme ambas, pues entonces, aunque tendré los Q 1,000 que estoy viendo, la CC contendrá Q 0.
En el lado opuesto, quienes se inclinan por tomar ambas cajas razonan como sigue: en este momento mi contraparte ya colocó el dinero en CC, sean Q 0 o sean Q 11000,000. No tiene sentido tomar únicamente la caja de los Q 1,000, puesto que ya nada cambiaría el contenido de CC. Así que, lo lógico, a todas luces, es llevarme ambas cajas. Sería una bobería perder la opción extra de lo que hay en CC.
Como hemos dicho, el planteamiento divide a las personas en dos tipos, en función de las creencias de cada quien. Específicamente, se ha dicho que las personas racionales escogerán ambas cajas, mientras que las más irracionales solo la cerrada. Si se parte de que un oráculo, o predictor, perfecto no puede existir, se podría pensar que las personas racionales tienen ventaja a la hora de decidir. Este aspecto de la racionalidad es algo que no debe tomarse a la ligera, ante una creciente actitud irracional en los colectivos, tanto en lo social, como en lo económico y lo político.
Respecto a la frase inicial, de Lerner, sobre posibles viajes en el tiempo, viene al caso recordar lo que el afamado astrofísico teórico, cosmólogo y divulgador británico, Stephen Hawking, decía:
Los viajes en el tiempo solían ser considerados como ciencia ficción, pero la teoría general de la relatividad de Einstein permite la posibilidad de que pudiéramos deformar tanto el espacio-tiempo que podrías disparar un cohete y regresar antes de que salga. Incluso si resulta que viajar en el tiempo es imposible, es importante que entendamos por qué es que esto es así, que comprendamos la imposibilidad.
Además de la cuestión lógica formal, se pone sobre la mesa lo que sucedería con un oráculo perfecto, sobre la temática filosófica de la omnisciencia, o el hipotético viaje al futuro que la ciencia ficción ha venido pregonando, en donde nos enteraríamos de lo que está por acontecer. En este collage de ideas se encuentra en juego la misma causalidad y el determinismo extremo. Uno de los aspectos más perturbadores de estas ideas cuestiona la posibilidad del libre albedrío humano: ¿existe o es tan solo una ilusión mental?
Desde el punto de vista de la Física, para resolver los problemas de las paradojas en los viajes a través del tiempo, que los puentes de Einstein-Rosen (agujeros de gusano) y otros fenómenos topológicos en el espaciotiempo harían posible, se menciona el principio de autoconsistencia desarrollado por el astrofísico ruso Ígor Nóvikov en la década de los ochenta. El principio afirma: «si un evento existiese y provocase una paradoja […] entonces la probabilidad de ese evento es cero». La teoría de los multiversos, así como la interpretación de la mecánica cuántica de los mundos múltiples (IMM), de Hugh Everett, recurren a principios similares, para resolver el asunto de la unicidad de la historia, o la existencia de muchas.

Sobre la posibilidad del oráculo, es notable una anécdota de Michel de Nôtre-Dame, Nostradamus, un boticario francés mayormente conocido por su libro Les Prophéties (Las Profecías), una colección de 942 cuartetas. Se cuenta que un cierto duque invita al adivino a cenar, preguntándole «dime eximio clarividente, si hoy comeremos del lechón rojo o del negro», a lo que el futurólogo contestó: «será del rojo». El noble, para ponerlo en aprietos, ordenó que mataran y sirvieran del negro. Llegada la cena, alardeando le dijo: «¡viste, has errado!». «Comemos del rojo», replicó Nostradamus. Llamando al cocinero, el duque preguntó: «Dinos, ¿qué comemos?» El cocinero aclaró que era del lechón rojo pues el negrito había sido envenenado por una serpiente.
La primera de las ideas contemporáneas para regresar en el tiempo, desde la perspectiva científica, provino de las nociones sobre una movilidad supralumínica, es decir, superando la velocidad de la luz. Sobre ello la física teórica estadounidense, Lisa Randall, especializada en partículas, teoría de cuerdas y cosmología, expresó: «Viajar más rápido que la velocidad de la luz puede tener, sin duda, implicaciones dramáticas, que son difíciles de entender, como los viajes en el tiempo». En contraparte, Herbert George Wells escribió en 1895, en La máquina del tiempo: «Usted no puede moverse de ninguna manera en el tiempo, no puede huir del momento presente».
No podríamos irnos sin pedirle al lector, lectora, que asuma su posición predilecta, pero que también ensaye a colocarse en la posición contraria. Circula una secuencia que muestra a una bailarina girando en un sentido. La animación invita a que te concentres para «verla» girando en sentido contrario. Se menciona una relación con los dos hemisferios cerebrales, el que es más intuitivo y el que es más racional. Pareciera que lo tratado mantiene un cierto símil con ello, vinculando la racionalidad con la creencia, de índole más irracional.
En suma, cabe comentar que la paradoja de Newcomb se encuentra al nivel de la famosísima paradoja de Russell, que establece una aporía que llama a una profunda revisión de las bases epistemológicas más fundamentales. Sobre la temática de esta oportunidad, el escritor y bioquímico de origen ruso, nacionalizado estadounidense, Isaac Asimov, expresó:
Sin la menor duda, tomaría ambas cajas [ pues ] soy determinista, [ dado que ] está perfectamente claro que cualquier ser humano digno […] preferiría el libre albedrío. [Seleccionar ambas cajas manifiestas] nuestra disposición a apostar por su no-omnisciencia, a favor de nuestro libre albedrío. […] Desde luego, si Dios ha fallado y ha dejado un millón […] en la caja, entonces no solamente ganamos el millón, sino que [ponemos] en evidencia que Dios no es omnisciente. [Al tomar] la segunda caja, se gana el condenado millón, [aceptando] ser esclavo por ello. ¡A nadie que obre así puedo yo reconocerlo como un humano digno!
Fuente de imágenes ::
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: https://www.cronicasdeunmundofeliz.com/2014/05/la-paradoja-de-newcomb-y-la-libertad-de.html + https://www.youtube.com/watch?v=jM6HKw4NgCQ + https://encyclopaedia.herdereditorial.com/wiki/Problema_de_Newcomb + https://es.wikipedia.org/wiki/Agujero_de_gusano
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: https://www.youtube.com/watch?v=HyQvySZUu0Q + https://es.wikipedia.org/wiki/Agujero_de_gusano
[ 3 ] Imagen editada por Vinicio Barrientos Carles :: https://www.taringa.net/+ciencia_educacion/la-paradoja-de-newcomb-y-una-posible-solucion_hwb9o + https://es.wikipedia.org/wiki/Agujero_de_gusano + https://www.youtube.com/watch?v=Ldngi2WtGik + https://www.youtube.com/watch?v=HyQvySZUu0Q + https://encyclopaedia.herdereditorial.com/wiki/Problema_de_Newcomb







