Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Las leyes de la matemática no son meramente invenciones o creaciones humanas. Simplemente son: existen independientemente del intelecto humano. M. C. Escher
En julio de este año la matemática ucraniana Maryna Sergiivna Viazovska fue galardonada con la prestigiosa Medalla Fields, que compite con el Premio Abel por el pedestal del máximo reconocimiento al talento y a la contribución científica que se otorga en esta disciplina. No obstante, mientras que la Medalla Fields, entregada cada cuatro años a profesionales de la Matemática, menores de cuarenta años, se viene concediendo desde 1932, el Premio Abel es más reciente, pues fue creado por el gobierno noruego en 2002, conmemorando el bicentenario del natalicio del genial matemático Niels Henrik Abel.
Para noticia de quien nos lee, en Matemática no existe concesión de Premio Nobel, por alguna curiosidad que en otra oportunidad tendremos a bien compartir, por lo que a estos premios se hace referencia, con relativa frecuencia, como equivalentes al Nobel en Matemática. Siempre que es posible damos merecida difusión a las científicas que son premiadas en ciencias formales o en Física, pues la brecha de género de los premios concedidos no hacen justicia al talento femenino. Por ejemplo, a la fecha, la proporción de mujeres laureadas en los galardones mencionados es inferior al 4 %.
Pues bien, en esta ocasión estamos citando a Viazovska porque, como explicábamos en «Maryna: tras las huellas de Maryam», a ella le fue concedido el reconocimiento Fields por sus valiosos aportes en la teoría de empaquetamiento de esferas en ocho y veinticuatro dimensiones, resolviendo una variante de la generalización derivada de la conjetura de Kepler. En este momento el lector y lectora se dirá para sus adentros: ¿pero qué es eso de una esfera en un espacio 24-dimensional? O como dicen los más jóvenes: ¿qué fuma esta gente para imaginar esas cosas? Con un poquito de mayor seriedad: ¿cómo es que se puede entender una realidad así? ¿a qué nos referimos con «multidimensionalidad»?

Alguno, alguna, podrá recordar algo que ha leído sobre la mecánica relativista, que habla del espacio tiempo, estableciendo, desde esa perspectiva, que nuestro universo físico es 4-dimensional, a diferencia de las tres dimensiones que aprendimos en la escuela elemental. Para lo que acá deseamos desenrrollar, es importante observar que las palabras son utilizadas, con gran facilidad, de muchas maneras, esto es, que asumen varias acepciones, que poseen distintos signnificados. Por ejemplo, cuando decimos: «es un problema de grandes dimensiones», la palabra «dimensión» la estamos utilizando como un sinónimo de tamaño.
Sin embargo, cuando decimos que un cilindro es un cuerpo tridimensional, o que se encuentra incrustado en un espacio de tres dimensiones, el significado de dimensión es uno matemático, geométrico o físico, puesto que deseamos expresar que este cuerpo sólido posee una medida para su largo, una para su ancho, y otra para su altura, o profundidad, como nos agrade más expresarlo. Es decir, estamos claros que una caja de carton corrugado es 2-dimensional (bidimensional), cuando está desarmada, pero ya armada alberga cuerpos sólidos, esto es, que son 3-dimensionales (tridimensionales).
Al reparar en el asunto, podemos objetar que, aún desarmada la caja tal, es tridimensional, pues el corrugado tiene grosor, al igual que una hoja de papel también lo tiene. Aunque el grosor es pequeño para nuestros sentidos, no es nulo. Nos percatamos que los cuerpos de una dimensión, los segmentos de recta, y los cuerpos de dos dimensiones, los planos, son realmente abstracciones realizadas en nuestra mente. Aún así, partimos del hecho de que, todos y todas, comprendemos lo que es una, dos y tres dimensiones espaciales. Empero… ¿y veinticuatro? En el artículo «Cuerpos multidimensionales» explicamos una de las acepciones matemáticas del concepto dimensión, una de tipo geométrico, basada en la noción de desplazamiento.
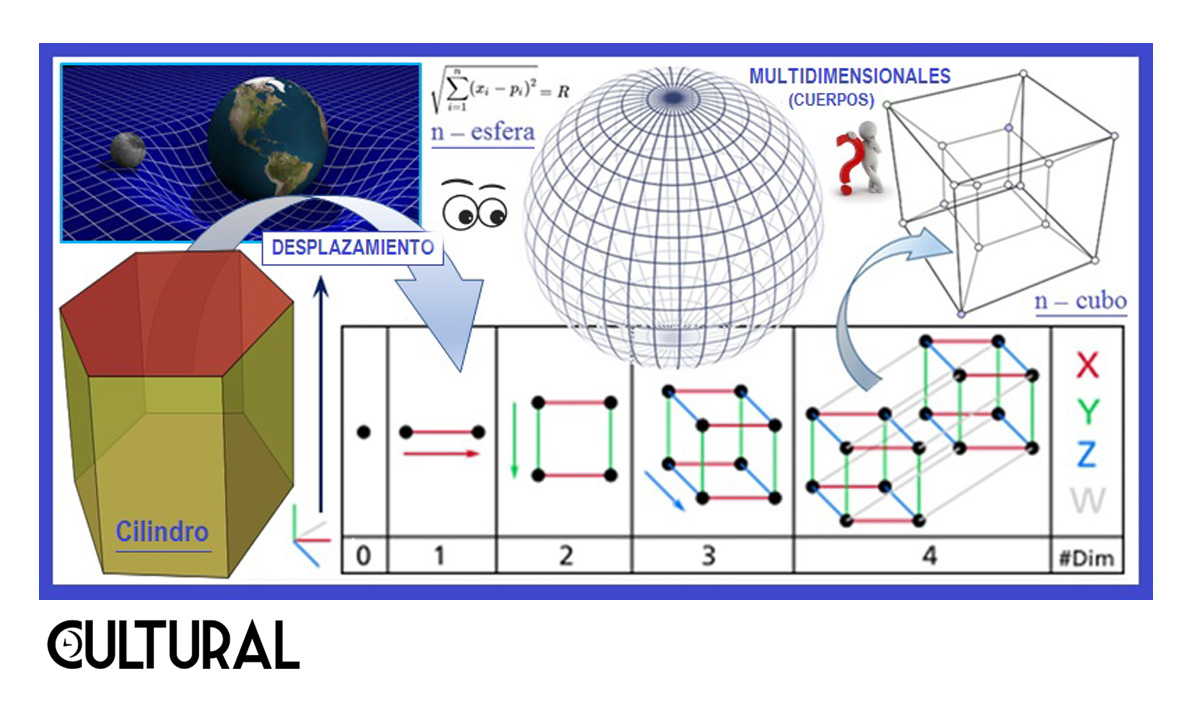
La intención de esta publicación, en Polítopos, es la de ilustrar que no resulta de otro planeta la comprensión de lo que podemos concebir como las varias dimensiones de un cierto objeto, sin entrar a grandes honduras o intrincadas teorías, posiblemente incomprensibles para el común de los mortales. Es más, superada la barrera de lo que, quizá, estamos imaginando como algo irreal, podremos ver que este concepto de la multidimensionalidad, surgido en la que Carl Friedrich Gauss denominó la reina de las ciencias, puede ser aplicado en distintos ámbitos, y que de hecho, quizá sin percatarnos, lo estamos usando en forma cotidiana. Para dar cierre al ámbito matemático, la Wikipedia nos informa:
La dimensión (del latín dīmensiō: medir) es un número relacionado con las propiedades métricas, o topológicas, de un objeto matemático. [ Específicamente, ] la dimensión de un objeto es una medida topológica del tamaño de sus propiedades de recubrimiento. [ Cabe aclarar que, ] existen diversas medidas o conceptualizaciones de dimensión: lineal, topológica, fractal…
En el epígrafe trajimos a colación al artista neerlandés Maurits Cornelis Escher, ampliamente conocido por sus grabados y dibujos de figuras imposibles, teselados paradójicos y de mundos imaginarios, en espacios más alla de las dos o tres dimensiones estándar. Escher finaliza la cita del inicio, anotando: «Lo más que puede hacer un hombre de inteligencia aguda es descubrir que esas leyes están allí y llegar a conocerlas». Cabe recordar que el artista figura como parte de una interesantísima obra, de Douglas R. Hofstadter, ganadora del Premio Pulitzer, a finales de los setenta: «Gödel, Escher, Bach: un Eterno y Grácil Bucle» (Gödel, Escher, Bach: an Eternal Golden Braid, abreviado GEB por el mismo autor).
En la anterior definición, conviene tomar la connotación más antigua, y quizá la más intuitiva, de lo que en Matemática se entiende por dimensión, para pasar luego a una generalización en otros contextos, que preserve las ideas fundamentales del concepto. Nos referimos a la dimensión lineal, utilizada en los espacios vectoriales, y estudiada en una de las ramas del Álgebra abstracta, denominada justamente Álgebra Lineal. Sin entrar en tecnicismos, este concepto fundamental de la dimensión de un espacio corresponde al que en la geometria elemental solemos utilizar, este que hemos descrito implicitamente al hablar del largo, ancho y alto de una cierta caja.

Pertinente incorporar al matemático y filósofo francés René Descartes, figura clave para la Modernidad, pues él introdujo en la geometría nociones clave, las que nos resultan bastante familiares, pues forman parte de los contenidos temáticos en los estudios básicos de la secundaria. Se trata de los sistemas coordenados, que vinculan la geometría euclidiana con los rudimentos algebraicos que a fines del siglo XVI iniciaban su desarrollo. Partiendo del hecho de que un punto en una línea recta queda determinado por el número real que indica su posición con respecto a un origen arbitrario, pasamos a determinar la posición de cualquier punto en el plano, o en el espacio, mediante dos o tres coordenadas, respectivamente.
Con lo anotado previamente, también nos percatamos de nuestra familiaridad con los mencionados sistemas de coordenadas cartesianas, que recurren, usualmente, a ejes perpendiculares previamente definidos. En este contexto, también resulta claro que el número de coordenadas requeridas para determinar la posición de un punto nos proporciona la dimensión del espacio en cuestión. Acá coexisten dos naturalezas, o estructuras formales, pues, por un lado, cada punto es un objeto geométrico, en un espacio euclidiano, pero, por el otro, es un objeto algebraico, en un espacio lineal, pues asociado se encuentra un vector, que imaginamos como una «flecha» que va del origen del sistema coordenado al punto en cuestión.
Esta correspondencia entre una naturaleza geométrica y otra algebraica, no solo es potente, analíticamente hablando, sino que es hermosa, pues integra áreas de estudio que uno podría imaginar disconexas. Empero, lo que acá nos interesa es la generalización que tenemos a la puerta de nuestro discurso. Sea que pensemos en las coordenadas del punto geométrico, o sea que pensemos en las componentes del vector algebraico, veremos que una generalización es posible y muy sencilla de realizar. En lugar de dos o tres, coordenadas o componentes, ponemos pensar en cuatro, cinco o un número natural cualquiera, dando lugar a espacios n-dimensionales, esto es, de dimensión n.
Entonces, según lo que hemos dicho, podemos aventurarnos a pensar que si establecemos una n-tupla de números, con alguna significancia empírica factual, estaríamos determinando un punto de un espacio multidimensional de n dimensiones. Esto, en el fondo, ya no nos parece tan extraño, puesto que estamos acostumbrados a manejar listas de datos (numéricos o de otro tipo) asociados a un cierto objeto. Por ejemplo, cuando llenamos una boleta de datos, nos piden que anotemos nuestro nombre, el sexo, la fecha de nacimiento, nuestra nacionalidad, la dirección domiciliaria, y si se tratara de una solicitud laboral, podrían preguntarnos el salario mensual que aspiramos obtener.
En el ejemplo, nos han pedido seis datos, por lo que inicialmente colocaríamos estos en una 6-tupla, esto es, en una línea con seis columnas, pensando en la usual hoja electrónica, a la que recurrimos para registrar estas listas, que denominamos coloquialmente «bases de datos», aunque aquí posiblemente deberíamos precisar este concepto. Cada persona y sus datos representaría un punto en un espacio de dimensión 6. Como es frecuente, podríamos codificar cada una de las «variables», de manera que cada campo o variable asumiría valores en un cierto rango. En este caso, cada una de las personas que solicitan trabajo sería un objeto 6-dimensional, estando el espacio correspondiente conformado por todas las posibles 6-tuplas.
Sin embargo, debemos agregar un asunto de cierta importancia, y es que, por un lado, no estaría bien que nos preguntaran nuestra edad, porque puede obtenerse de la fecha de nacimiento. Por el otro, lo que hemos denominado «nombre» podría desglosarse en otros campos, por ejemplo, en nombre y apellido. Reflexionando, veremos que la dimensionalidad de un objeto tiene está vinculada con este concepto que hemos venido citando: determinación. Las interrogantes al respecto son abordadas desde la estadística y la contemporánea ciencia de datos, ahora en boga a raíz de la implementación de potentes algoritmos basados en las técnicas del aprendizaje automatizado.
Esta noción de determinación está vinculada con otra, la de independencia, que podemos explicar desde nuestro punto de partida, los cuerpos geométricos elementales. Piénsese en un rectángulo. Decimos que es un objeto bidimensional porque no podemos especificarlo con una única medición. Supóngase, por ejemplo, que proporcionamos el área y que esta vale 100. Con esta información vemos que el rectángulo no está determinado. El lector o lectora puede verificar que muchos rectángulos distintos tienen área 100. Unos más altos, otros más largos. Las dos dimensiones son independientes, puesto que, dado el largo de un rectángulo cualquiera, nadie podría saber cual es su ancho. La total indeterminación implica la independencia.
Igual sucedería si damos la diagonal del rectángulo. No queda determinado porque este cuerpo es bidimensional. Se necesitan dos datos independientes para determinarlo. Similar sucede si proporcionamos el apellido de una persona. ¿Podríamos de ello saber su nombre? O de manera más transparente, dado el sexo de un ser humano, ¿podría establecer su estatura? Decimos que existe independencia entre las variables. Las dimensiones de un objeto refieren a aspectos en lo absoluto independientes, como en el largo, el ancho y la altura de una caja. Por el contrario, descubrimos que la masa y la estatura de una persona no son tan independientes. Decimos que existe alguna correlación estadística.
Esta dependencia última se ve reflejada en las tablas predictivas que establecen la masa ideal que debería tener un ser humano, si se conoce su sexo, su edad, su estatura y la actividad física que lleva a cabo. Desde este punto de vista, el peso ideal (la masa) de una persona es un objeto tetradimesional, de dimensión 4, siendo los factores o componentes las cuatro variables mencionadas. La dimensionalidad, formal o factual, de un cierto objeto o variable, es algo que puede investigarse estadísticamente mediante el análisis de componentes principales.Verifique quien nos lee que un color es tridimensional, pues puede ser determinado por tres coordenadas, lo que se aprecia al consultar la paleta de su ordenador.
Para ir cerrando, en la imagen N° 3 se ilustran varias ideas fuerza sobre este tema. Arriba, en la izquierda, se alude al sesgo cognitivo del fenómeno de la reducción dimensional: cuando un cilindro se «aplasta» en dos dimensiones, se obtendrán visiones parciales no compatibles. Esto sucede frecuentemente en el análisis del posicionamiento político, pues se insiste en ubicar a las personas en una única dimensión (en el eje izquierda-derecha), cuando un espectro político actual requiere de más de tres dimensiones: lo social, lo económico, lo ambiental, lo cultural… Abajo, en la izquierda, un esquema del espacio-tiempo, donde el espacio está reducido a dos dimensiones, como suele presentarse. En la derecha, la muy citada multidimensionalidad del ser humano.
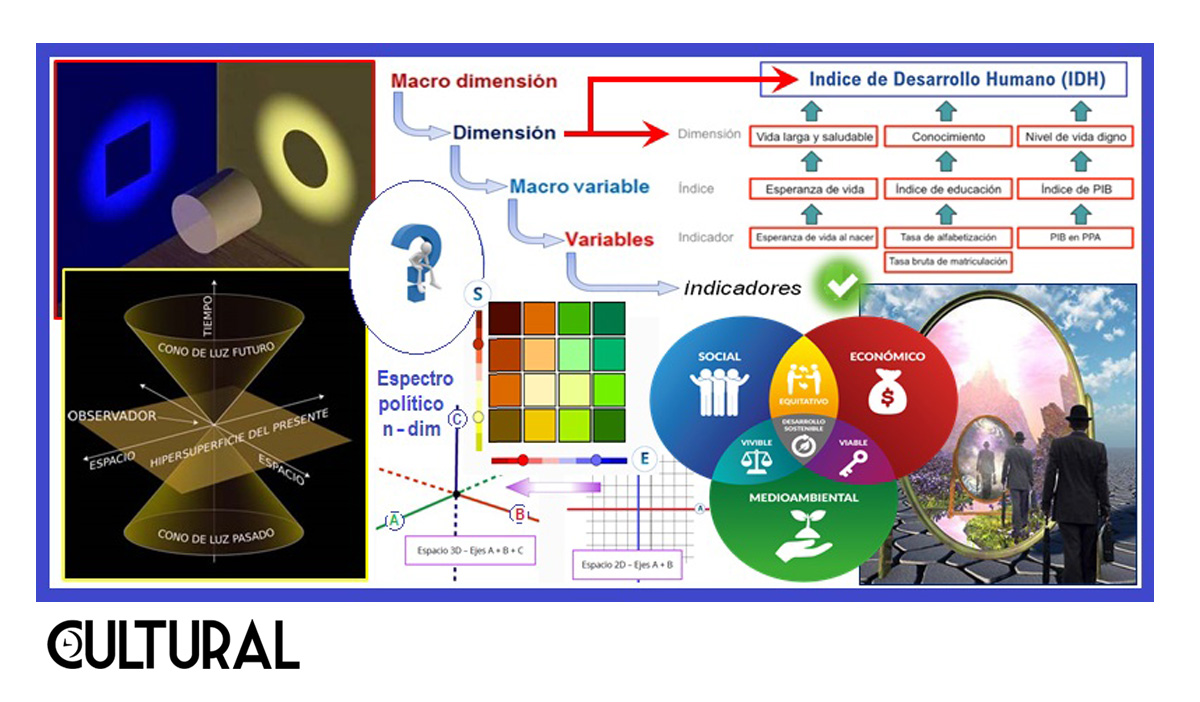
También se muestra un ejemplo de índice multidimensional: el Índice de Desarrollo Humano, IDH. El modelo establece que el «desarrollo» es un objeto tridimensional, que significa que para medir el desarrollo de un Estado o país se deben determinar los valores en tres dimensiones, o componentes. Se asume que estas dimensiones son independientes y a su vez exhaustivas, esto es, que describen completamente el fenómeno que se desea medir. Se muestra también un esquema para la definición de las variables que integran una cierta dimensión, y los indicadores como los métodos de cuantificación. Otros ejemplos de objetos multidimensionales son la pobreza, la inteligencia, el rendimiento académico, el desempeño laboral, la gestión institucional y muchos otros más.
Sobre el epígrafe, de Escher, que expresa en palabras lo que el artista plasmaba en muchos de sus dibujos, conviene citar a Hofstadter, quien sobre las motivaciones para escribir su libro, expresó:
Me di cuenta de que Gödel, Escher y Bach eran solamente sombras dirigidas en diversas direcciones de cierta esencia sólida y única. Intenté reconstruir el objeto central, y quise plasmarlo en este libro.
___________________________
Fuente de imágenes ::
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: http://cientificoficial.blogspot.com/2017/11/la-relatividad-de-einstein-la.html + https://videoganancias.wordpress.com/2017/01/31/diferentes-puntos-de-vista/ + https://inteligenciaemocionalisei.wordpress.com/multidimensionalidad/ + https://es.wikipedia.org/wiki/Variedad_de_Calabi-Yau + https://es.wikipedia.org/wiki/Prisma_(geometr%C3%ADa)
[ 2 ] Tomada de gAZeta, editada Vinicio Barrientos Carles :: https://gazetagt.com/cuerpos-multidimensionales/
[ 3 ] Imagen editada por Vinicio Barrientos Carles :: http://cientificoficial.blogspot.com/2017/11/la-relatividad-de-einstein-la.html + https://videoganancias.wordpress.com/2017/01/31/diferentes-puntos-de-vista/ + https://inteligenciaemocionalisei.wordpress.com/multidimensionalidad/








