Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
La naturaleza es una esfera infinita, cuyo centro está en todas partes y la circunferencia en ninguna.
Blaise Pascal
Arquímedes de Siracusa (n. 287 a. C) fue un físico, astrónomo, filósofo, matemático, ingeniero e inventor griego. Aunque se conocen pocos detalles de su vida, es considerado uno de los matemáticos más importantes y notables de la Antigüedad, y, en general, de toda la historia. Siracusa, Συρακοῦσαι, su ciudad natal, en donde vivió y falleció, está ubicada en la costa sudeste de la isla de Sicilia, en el Mediterráneo central italiano. Su nombre, Ἀρχιμήδης está formado por las palabras αρχι (archi), que significa origen o dominio, y Ημαδομαι (emadomai), que significa preocuparse, de donde el nombre «Arquímedes» viene a traducirse como «el que se preocupa». Sobre este genial personaje, en la Wikipedia, se lee lo siguiente:
Entre sus avances en física se encuentran sus fundamentos en hidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo que lleva su nombre. Experimentos modernos han probado las afirmaciones de que Arquímedes llegó a diseñar máquinas capaces de sacar barcos enemigos del agua o prenderles fuego utilizando una serie de espejos. Destaca el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número pi. También definió la espiral epónima, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy grandes.
Arquímedes murió durante el sitio de Siracusa (214-212 a. C.), siendo asesinado por un soldado romano, a pesar de que existían órdenes explícitas de que no se le hiciese ningún daño. Sobre su vida de se han escrito numerosas anécdotas y existen diversas leyendas, de las que no se sabe cuánto en ellas podría ser verdad y cuánto son producto de la ficción a lo largo del tiempo. El caso es que los historiadores más serios han documentado la fama y posición que Arquímedes de Siracusa gozó en vida.
En este sentido, conviene señalar que su reputación de científico y notable inventor no provino de su linaje o de alguna influencia política específica, sino que fue el resultado directo de las variadas acciones que tuvieron un impacto favorable en los pueblos que le circundaban, en particular en su ciudad natal, donde vivió con el reconocimiento de un estatus de ciudadano magnífico.
Entre estos alegóricos relatos, situados entre la tradición histórica y la leyenda, se encuentra uno que habla de una serie de inventos que posibilitaron la defensa de Siracusa por más de una década, impidiendo que los romanos pudieran ocuparla. Según la narrativa, el inventor griego creó un sistema de reflectores, los llamados espejos ustorios, que reflejaban la luz y la radiación solar, concentrando la energía térmica consecuente sobre los barcos enemigos, con la finalidad de incendiarlos en el momento oportuno. A manera de cañones térmicos, los barcos del enemigo no lograban traspasar más allá de ciertos límites.

Otro relato habla de la forma en que murió, y, aunque existen varias versiones del hecho, se sabe que su fallecimiento aconteció cuando la ciudad fue tomada por los ejércitos romanos, comandados por el general Marco Claudio Marcelo. Una de las varias versiones relata que, cuando un soldado pretendía arrestar al eximio pensador, el geómetra hizo caso omiso de la orden de conducción, en vista que este se encontraba absorto contemplando un diagrama matemático, limitándose a solicitar no perturbar su concentración y que se le otorgara un poco más de tiempo para resolver el problema en el que se encontraba trabajando.
En esta versión de lo sucedido, el soldado, enfurecido ante la respuesta, mató con su espada, en colérica reacción, al magnánimo matemático, quien, se dice, profirió como sus últimas palabras, las que usualmente son citadas en latín: Noli turbare circulos meos (No perturbes a mis círculos). Lo que sí se encuentra perfectamente documentado es que el general Marcelo se mostró furioso ante el fatídico asesinato de Arquímedes, contrariando en lo absoluto las órdenes por él giradas, en torno de respetar la vida y no herir al matemático, debido a que lo consideraba un valioso activo científico, a quien deseaba conocer en persona y tener de su lado.
De todos los aportes e investigaciones que Arquímedes realizó a lo largo de su vida, hay un logro por el que él guardaba especial aprecio, puesto que, al parecer, le provocó mucho orgullo y satisfacción el haberlo descubierto y demostrado. Para el geómetra griego, el descubrimiento de la relación existente entre el volumen de la esfera, el cono y el cilindro tuvo un singular y sobresaliente impacto. El matemático comprobó, de varias formas, que tanto el volumen como el área de la esfera son exactamente dos terceras partes del área y el volumen del correspondiente cilindro circular que la circunscribe, respectivamente. En esta ocasión, además de las pinceladas históricas que estamos dando, tenemos por objetivo ilustrar este particular teorema.
Una métrica de la significancia que tuvo para el polímata griego la relación existente entre los volúmenes de los tres cuerpos redondos, puede obtenerse de una de sus solicitudes postreras, pidiendo que en su tumba se colocará una escultura y unos grabados que hicieran alusión al formidable hecho matemático. En el año 75 a. C., el orador, político y filósofo romano Marco Tulio Cicerón tuvo a bien visitar la tumba del erudito, constatando que, en efecto, sobre ella se había colocado una esfera inscrita dentro de un cilindro, conteniendo, además, unos diagramas con resultados matemáticos diversos.
La hoja de ruta estándar para establecer que el volumen de la esfera es dos terceras partes de lo correspondiente para el cilindro circunscrito empieza con el cálculo volumen del cono. Primero se establece que todo cono, circular o no, es la tercera parte del cilindro que lo circunscribe. Igual sucede con una pirámide cualquiera y el prisma respectivo. Paso seguido, se demuestra que el cono y la esfera juntos, es decir, sumados, equivalen al cilindro. De lo anterior, se concluye que, si el cono es una tercera parte del cilindro, la esfera deberá ser, por lo tanto, las dos terceras partes, estableciendo así la relación 1:2:3 entre los citados cuerpos cono:esfera:cilindro.
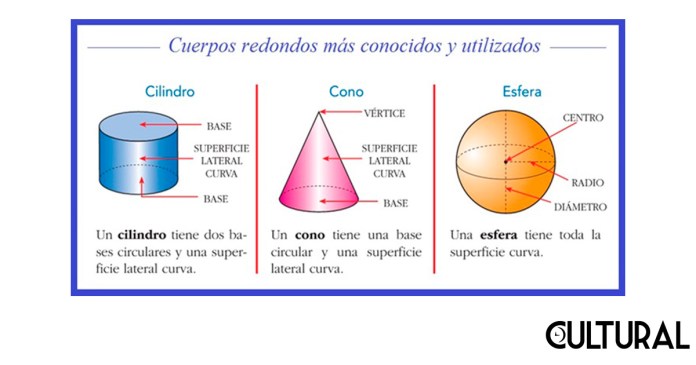
En torno de estos asuntos, como al lector y lectora seguramente le aconteció, en su momento tuvo que memorizar algunas fórmulas que le permitían el cálculo del volumen y del área de los tres cuerpos redondos presentados, mostrados en la imagen precedente, en vista que el concepto de estudio que se manejaba, y que se sigue manejando, lastimosamente, en el sistema educativo tradicional, es el de la memorización y la posible aplicación de todo cuanto el maestro o la maestra pide que se aprenda.
Sin embargo, los pobres resultados de tales conceptos y visiones de lo que se interpreta por «educación» son, hoy por hoy, visibles y palpables, para todos y todas, puesto que, de la totalidad de estos esfuerzos, nada o casi nada permanece, como cualquiera podría constatar. En complemento a la gravedad, también podríamos percatarnos de que las escasas excepciones a esta regla, es decir, que las personas que aún recuerden estas fórmulas, que en su momento fueron percibidas como extraños artilugios, no poseen una sencilla explicación que justifique tales algoritmos, una falencia que también puede ser apreciada en los profesionales con especialidades en temas u orientaciones de índole cuantitativa, como es el caso de los ingenieros.
En dirección contraria, la simplificación a la que lleva la comprensión de los hechos matemáticos más fundamentales es la llave crucial para su estudio, su recuerdo y perfecta utilización en aspectos de la vida cotidiana. Así, de forma particular, existen varias ideas clave con las que es posible facilitar el aprendizaje de la medida del tamaño de los distintos cuerpos y figuras geométricas. El primer punto clave es que la medida de la magnitud de un determinado cuerpo viene dada por el producto de sus dimensiones, o una fracción de este consabido producto.
Así, por ejemplo, tenemos que un rectángulo es el producto de su base por su altura, de similar forma que un triángulo es la mitad de este producto. Un segmento bajo un arco de parábola es dos tercios del rectángulo que lo circunscribe, como hemos podido hacer ver en una publicación precedente al respecto de la cuadratura de la parábola. Como en estos ejemplos se trata de un área, medida en unidades cuadradas (o sea cantidad de cuadraditos), el resultado vendrá dado por la multiplicación de dos medidas lineales.
Por otro lado, de manera similar, en tres dimensiones, el tamaño de una caja, un paralelepípedo, vendrá dado por el producto del área de su base por su altura. Esto es, como ahora se trata de un volumen, o sea, una cantidad de cubitos, la base será un área, en unidades cuadradas, que, multiplicada por la altura, en unidades lineales, dará como resultado una cantidad en unidades cúbicas, expresando el volumen. Similar en el cilindro, o en cualquier tipo de prisma, en tres dimensiones, la fórmula será siempre la misma, a saber: el área de la base, bidimensional, por la altura, de dimensión lineal. Esto se cumplirá en cualquier número de dimensiones, como nos podemos imaginar.
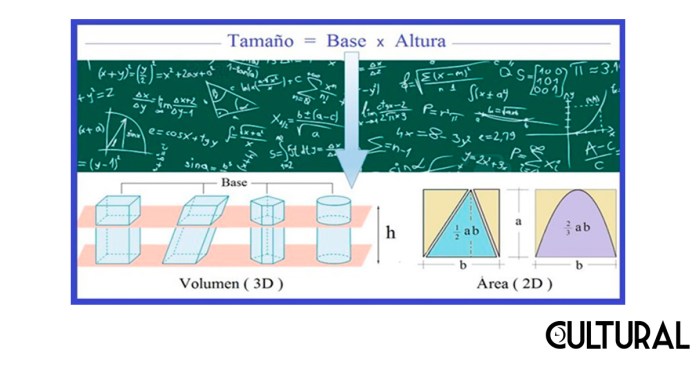
Conociendo el resultado fundamental de que el tamaño de un cuerpo es básicamente el producto de la magnitud de su base por la medida de su altura, puede uno reparar en relaciones interesantes entre ciertos cuerpos que se encuentran naturalmente vinculados entre sí. De esta manera nos ahorramos muchas aparentes complicaciones en la metodología del aprendizaje ciego de sendos formularios, que no nos dicen nada, derivando en colecciones de expresiones totalmente sin sentido. Por ejemplo, todo rectángulo puede dividirse en dos triángulos rectángulos congruentes, del mismo tamaño, a diferencia de un arco parabólico, una curva de grado dos, que resulta dividida en dos segmentos parabólicos de tamaño un tercio y dos tercios del tamaño del rectángulo en cuestión.
De similar forma, una curva cúbica, de grado tres, dividirá a un rectángulo en dos segmentos cúbicos, de grado tres, de tamaño un cuarto y tres cuartos, y así en lo sucesivo con curvas de grado superior. Para el caso que ahora nos ocupa, el de los tres cuerpos redondos tridimensionales, el hecho fundamental viene dado por la relación entre el tamaño del cono con el del respectivo cilindro que lo circunscribe. Si el área de un triángulo es la mitad de la del rectángulo que lo contiene, el volumen del cono viene a ser la tercera parte del cilindro. Los divisores dos y tres corresponden con las dos y tres dimensiones respectivamente.
En este sentido, deseo honrar a una fabulosa maestra que tuve la oportunidad de tener en mi formación primaria, quien me hizo la observación sobre este divisor-denominador dos para dos dimensiones, y el divisor-denominador tres para tres dimensiones, como una forma comprensiva de introyectarlo, a la vez de representar una razonable propiedad mnemotécnica. Recuerdo que, para aquella ocasión, mi recordada y apreciada maestra llevó un vasito de cono y un vaso cilíndrico de casi igual tamaño en su base. Llenando el cono de agua preguntó: ¡¿con cuántos vasitos de cono creen que se pueda llenar este cilindro de la misma altura?!
Procedió a verificarlo, obteniendo, como gran moraleja, que no eran dos los vasitos requeridos… , ¡sino tres! Por otro lado, dejaba la estimulante sugerencia, sobre las mentes más inquietas, que, si se tratara de un mundo con cuatro dimensiones, y tuviéramos el respectivo cuerpo similar al cono, el tamaño de este sería la cuarta parte del correspondiente cilindro. Si se investiga, podremos constatar que esta es efectivamente la situación, un poco más allá de nuestras percepciones sensibles, pero tal y como matemáticamente es factible demostrar. En parte, al recordarlo, veo que para una educación de calidad deberíamos contar con maestros y maestras excelentes y creativas como estos recuerdos que comparto hacen ver.
En fin, que esta relación permite calcular el volumen del cono y de la esfera, siempre que apliquemos para el cilindro el principio de que su volumen viene dado por el producto de su base, entiéndase un círculo (π r2) multiplicado por la altura. Entonces, el cono tendrá un volumen de la tercera parte de este resultado, siendo la esfera del doble que el respectivo cono, de manera que sumando el cono más la esfera tendremos un total equivalente al cilindro, y ese es el fundamento para el diagrama observado en la tumba del Arquímedes, mostrado en una de las imágenes del artículo.
Se podrá observar que, en este caso en particular, dada la relación de inscripción y circunscripción, tanto el cilindro como el cono, ambos con bases circulares y rectos, puesto que sus ejes son perpendiculares a sus bases, tienen como peculiar altura una equivalente al diámetro de la esfera, para poder coincidir de forma tangencial.
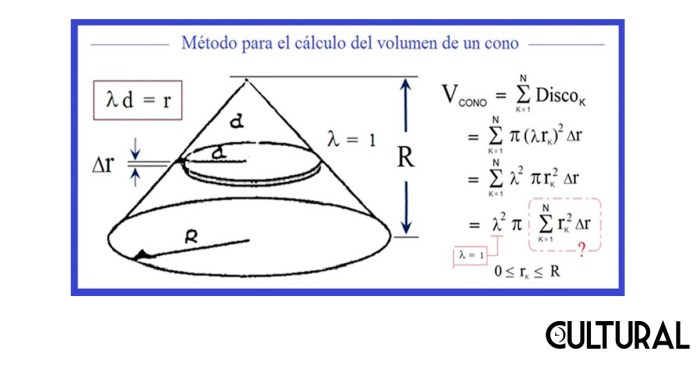
Para establecer esta relación de la tercera parte, Arquímedes desarrolló, con su método exhaustivo, una suma infinita para determinar, finalmente, que la fracción apropiada para el volumen del cono es cabalmente 1/3. Este método es semejante a como se hace ahora en un curso moderno de Cálculo Integral, como cualquier joven estudiante podrá constatar. El punto crucial para la sumación, seleccionada con la interrogante en rojo en la imagen precedente, está íntimamente conectada con el área de un segmento parabólico, problema que el matemático griego había ya resuelto previamente, como hicimos ver en nuestro artículo anterior.
Este método de agotamiento o exhaución le permitió a Arquímedes realizar exitosamente operaciones para el cálculo con superficies y volúmenes curvos, sentando las bases para el posterior Cálculo Infinitesimal de la Edad Moderna, desarrollado en el siglo XVII, de manera simultánea, por el británico Isaac Newton y el alemán Gottfried Leibniz.
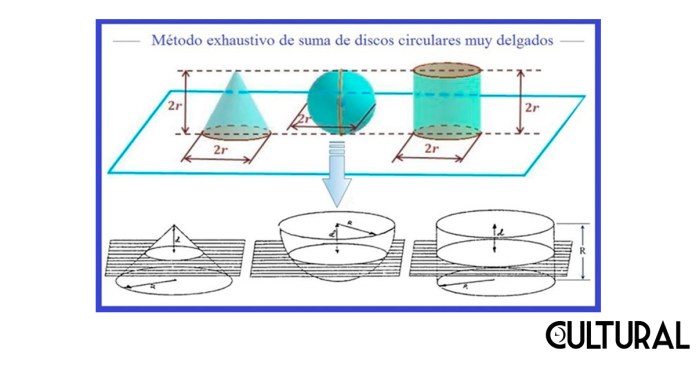
En el caso de los cuerpos redondos, este método considera la suma, integración, de una cantidad de discos circulares, cilindros delgados de altura Δh, los cuales se van haciendo, por un lado, mayores en cantidad, y por consiguiente, de un grosor cada vez más pequeño, de manera que, «en el infinito», se obtendrán como totalidad las curvas y formas que se pretende medir. El caso que acá se plantea, el del volumen del cono, es tan solo un ejemplo de la aplicación de tal método. Se tiene un paso teórico «al infinito», que posteriormente devendría la denominada operación analítica de tomar límites.
La esencia de la primera parte de la prueba radica en establecer que el volumen del cono será una fracción del correspondiente volumen del cilindro, fracción que se demuestra ser exactamente igual a un tercio (1/3), de forma que: VOLCONO = 1/3 VOLCILINDRO. Otra forma de decirlo es que los correspondientes volúmenes están en relación de uno a tres, esto es 1:3.
Si se parte del hecho fundamental de que el tamaño de un cuerpo tipo prisma, obtenido del despla_zamiento dinámico y paralelo de una superficie o línea, es básicamente el producto de la magnitud de su base, la medida de la superficie o línea que se desplaza, por la medida de su altura, la longitud del desplazamiento efectuado, podremos vincular ambos resultados para concluir que el volumen de un cono es un tercio del área de su base, que es un círculo (π r2), por su altura. En símbolos, de manera más sintética, se tiene que: VOLCONO = 1/3 Bh = 1/3 π r2 h. Esta es la fórmula que se encuentra en los manuales de los que hemos hablado anteriormente.
Para determinar la suma de una cantidad inmensa (¿infinita?) de delgadísimos discos (infinitesimales), tipo láminas, es necesaria una expresión algebraica que podamos manipular en el límite, es decir, cuando se imagina que tomamos un número de tales láminas que crece sin cota. El punto crucial para la sumación, seleccionada con la interrogante en rojo, en la imagen que sigue, estará íntimamente conectada con el área de un segmento parabólico, como se indica. Para Arquímedes esto resultó notable, y muy estimulante, pues él fue el primero que realizó el cálculo del área de un segmento parabólico, como ilustramos en la publicación sobre la parábola y su correspondiente cuadratura.
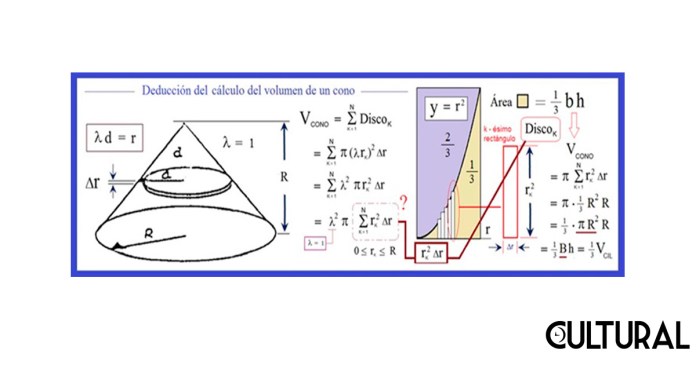
En la Matemática de ayer y hoy es clásica y característica la traslación de un cierto tópico, área, disciplina o problema a otro que no evidencia una conexión de una forma inmediata. Así, un problema determinado se ve transformado en otro, de manera que, al resolver este segundo, el primero queda total, o parcialmente, resuelto. En el caso de esta oportunidad, se observa cómo calcular el volumen de un cono circular recto, cuya altura coincide con el radio de la base, se transforma en otro, que es el de calcular el área de un segmento parabólico.
En lenguaje más analítico y menos geométrico, como suele usarse hoy en día, se transforma el cálculo del volumen del cono se transforma en el cálculo bajo una curva de segundo grado, un arco de parábola. Como se aprecia en la imagen previa, cada lámina circular tiene área π r2, y se trata de sumar, integrar, todas estas áreas a lo largo de una altura R. Esta suma de π r2 se convertirá en el área amarillo marrón de la imagen, la que justamente Arquímedes había calculado previamente y en la cual aparece la esperada fracción 1/3.
Recordaremos que, para el caso del tamaño de un triángulo, se usa la fracción un medio (½). Mencionamos que, en el análogo para un cono, la fracción a utilizar será de un tercio (1/3). Usando el problema homólogo del cálculo bajo un área, se tiene que, bajo una recta, una curva de grado 1, tendremos una fracción de un medio (1/2), mientras que, para el volumen del cono, ha resultado el área bajo una parábola, una curva de grado 2, y de ahí que la fracción resultante sea de un tercio (1/3).
Por ello mencionamos la expectativa natural, de forma que bajo una curva de grado 3 seguramente se obtendrá un área equivalente a una fracción de un cuarto (1/4) del rectángulo que la circunscribe, y así sucesivamente para curvas de una grado mayor, que es justamente lo que enuncia la denominada fórmula de cuadratura de Cavalieri, denominación epónima por el matemático italiano Bonaventura Cavalieri, discípulo de Galileo Galilei, quien la planteara explícitamente por vez primera en el siglo XVII, muchos siglos después de su precursor, el geómetra de Siracusa que hoy estamos elogiando.
El término cuadratura es un término tradicional utilizado para el área, como hemos explicado, pero en general puede referirse a la suma exhaustiva a lo largo de un cuerpo curvo, lo que a su vez puede reproducir el tamaño de un cierto cuerpo. Un caso particular de una curva de grado n ha sido el de la parábola, en la cual el trabajo de Arquímedes es trascendental. En términos generales, una integral se podrá interpretar geométricamente como el área bajo la curva en cuestión, y esto nuevamente es un magnífico logro arquimediano, plasmado en el tratado enviado a Dositeo de Pelusio, en la forma epistolar.
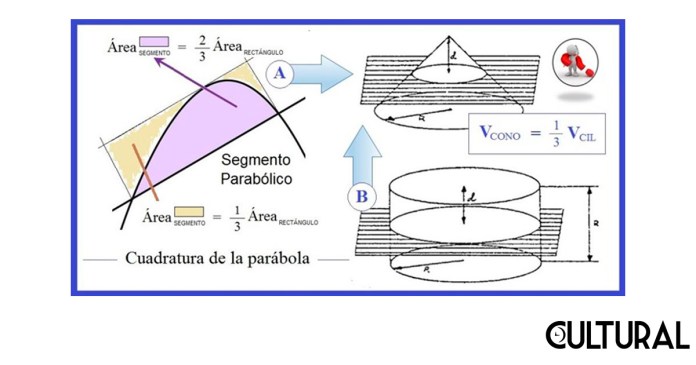
Resumiendo lo previo, para pasar a la esfera, hemos comprendido que las fracciones de un medio y un tercio, para las dos o tres dimensiones, en el cálculo del tamaño de un triángulo, área, y un cono o pirámide, volumen, provienen de la consideración de una suma infinitesimal de una recta o una parábola. Una plausible generalización es factible para el tamaño de uno cono más general, en un espacio n-dimensional, lo que no deja de ilustrar, de muy buena manera, el mundo abstracto de la Matemática.
La redondez que hemos tratado mediante capas infinitesimales, o discos infinitamente delgados, adquiere su máxima expresión en la esfera, redonda por todos lados. En este sentido, todas y todos estamos familiarizados con una pelota. De hecho, probablemente no hay juguete más popular y exitoso como una bola con la cual jugar. El concepto de redondez que encierra es también muy natural, tanto como el de rectitud, o casi rectitud, de un segmento de línea.
En este sentido, los antiguos geómetras griegos intentaron desarrollar un sistema geométrico completo, basándose únicamente en la regla y el compás, y no solo para efectos de constructividad o trazado, sino también en el sentido formal de utilizar como objetos primarios a los segmentos de recta y a los arcos de circunferencia. Esto se vio reflejado en la geometría euclidiana tradicional mediante la expresión «con regla y compás».
Por otro lado, al estudio de los cuerpos tridimensionales más elementales se le denomina estereometría, en el cual, como puede observarse, se ha substituido el prefijo geo, tierra, por el de estéreo, sólido. De manera particular, la estereometría estudia el volumen y superficie de los llamados cuerpos redondos, entre los que se ubican los más conocidos: el cilindro, el cono y la esfera. Para aproximarnos a la esfera, hemos tratado el caso del tamaño de un cono, que, como hemos visto, ha resultado ser, exactamente, la tercera parte del tamaño del correspondiente cilindro circunscrito, insistiendo que este factor reductivo de tres corresponde al número de dimensiones, matemáticas y físicas, en el cual existen este cono y el correspondiente cilindro.
El proceso de exhaución, que en el límite implica una sumación infinita de componentes de tamaño infinitesimal, se ilustra en la imagen que sigue. De esta forma, los cuerpos redondos de nuestro interés se visualizan como la integración de una cantidad muy grande de delgadísimas láminas de forma circular, en donde será clave el control del tamaño de tales discos, súper delgados. Relevante apuntar que los conceptos de cubo, esfera y cono pueden ser generalizados a un número natural arbitrario de dimensiones, en cuyo caso suele hablarse de hipercuerpos, como en el particular de la hiperesfera, una esfera en espacios n-dimensionales.
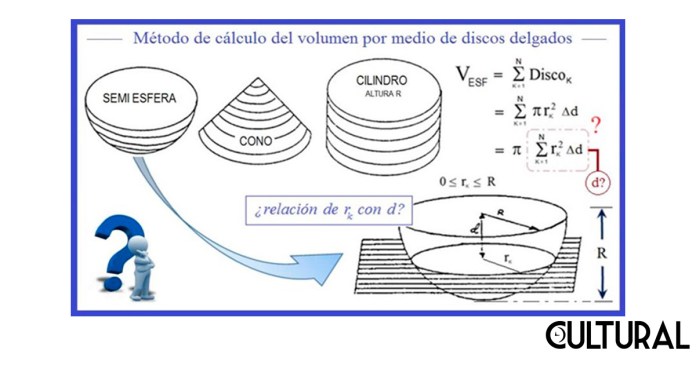
En la situación que nos atañe, el de la esfera 3-dimensional (bola), deseamos integrar los discos delgadísimos que la conformarían. Para este objetivo resultara imprescindible encontrar la funcionalidad, o dependencia, que tiene el radio de cada disco tiene. Puede observarse que, si se tratara de un cilindro, el radio de cada disco es constante (R en la imagen), mientras que en los casos del cono y de la esfera, estos radios son de magnitud variable. En el caso del cono, el radio será igual a la distancia entre la cúspide, o vértice, del cono y la posición del disco correspondiente. Esta altura aparece identificada en las imágenes, previas y siguiente, como d. La imagen que sigue es clave para la demostración de que el cono más la esfera totalizarán igual que el cilindro.
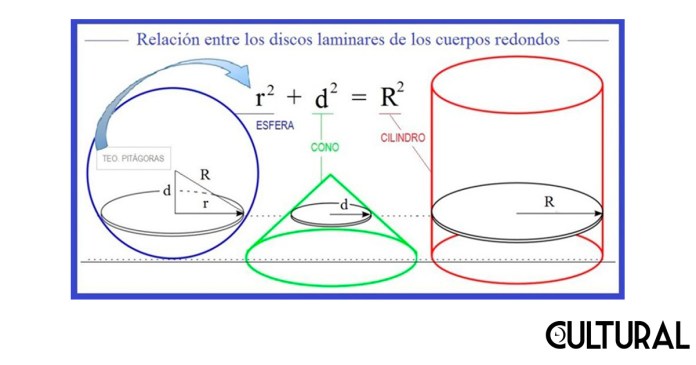
El secreto para la demostración requerida proviene del triángulo dibujado en la esfera. Véase la imagen previa, del lado izquierdo. Por el conocido teorema de Pitágoras es posible establecer una relación entre los radios de los discos en el cono y en la esfera, respectivamente, esto es, entre d, r y R. Como puede verse, la suma de los cuadrados de los radios del cono y de la esfera suman una constante, que es el cuadrado del radio R del cilindro. Esto implicará algo verdaderamente hermoso: que el área del disco de la esfera sumada con el área del disco del cono dará como resultado el área del disco del cilindro correspondiente. Recuérdese que el área de un círculo es proporcional al cuadrado de su radio: π r2.
El desarrollo formal de la prueba se esboza en la imagen siguiente. Se muestra cómo el volumen de la esfera sumado con el volumen del cono correspondiente totaliza el volumen del cilindro que circunscribe a ambos. Si a esta aseveración agregamos lo anotado arriba, que el volumen del cono es la tercera parte del volumen del cilindro, se podrá concluir que la esfera medirá dos tercios de este cilindro, en vista de que 1/3 + 2/3 = 1. Como muestra, esto implicará que la esfera de nuestro caso, que es una esfera cualquiera, mide, siempre, el doble del volumen de un cono que tenga por radio el mismo de la esfera en cuestión, y por altura el mismo valor.
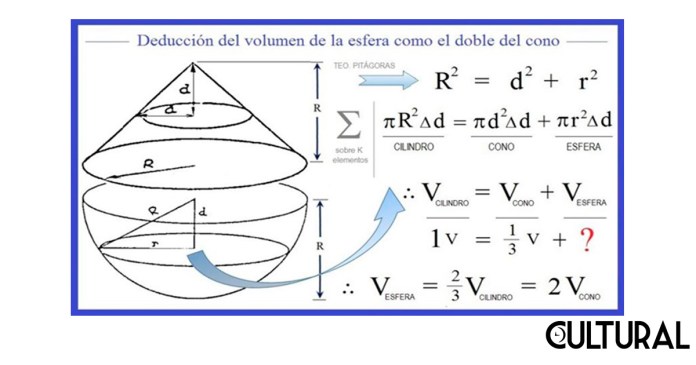
Como expresamos al inicio, aparentemente este hecho sorprendió grandemente a Arquímedes, a tal punto que pidió que se colocara en su tumba un modelo tridimensional, una escultura, que hiciera alusión al notable hecho. También mencionamos que la relación de dos terceras partes, entre la esfera y el cilindro, no solo se refiere a la medida de su volumen, sino también con relación al área, cuestión que no desarrollaremos en detalle acá. En otras palabras, si deseas saber cuál es el área o el volumen de una esfera, únicamente debes calcular lo correspondiente al cilindro circunscrito y tomar las dos terceras partes.
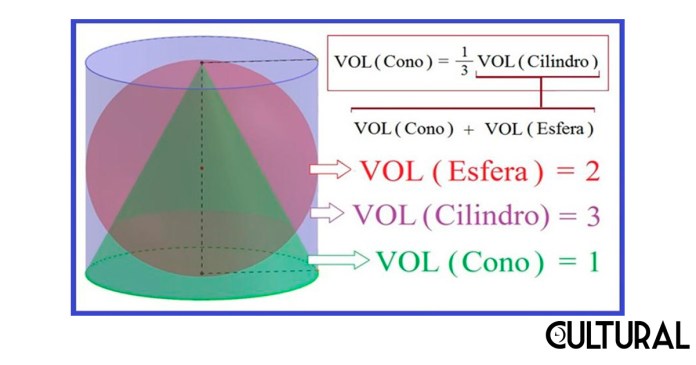
Incluimos ahora un diagrama que sintetiza estas interesantes relaciones métricas, vinculando los volúmenes de los tres populares cuerpos redondos tridimensionales, en el sentido que, si el cono midiera una unidad, la esfera mediría, sin posibilidad de error, exactamente el doble, es decir dos unidades, para totalizar un total de tres unidades para el cilindro correspondiente. A esto nos referíamos con que la relación cono:esfera:cilindro es exactamente 1:2:3.
Ahora, para cerrar, realizar una digresión y referirnos al epígrafe, en torno de la idea de una esfera, desde la filosofía y el pensamiento. La cita corresponde, en lo reciente, a una mención y análisis que el escritor y ensayista Jorge Luis Borges hiciera de un texto del matemático, físico, filósofo, teólogo católico y apologista francés Blaise Pascal. El ensayo de Borges tiene por título «La esfera de Pascal». No obstante, la consideración del cosmos como una esfera tiene su origen en los pensadores presocráticos. En particular, destaca Jenófanes de Colofón, quien, en absoluto desacuerdo con la visión antropomórfica de los dioses, dominante en su tiempo, decide plantear un único Dios, a quien propone como «una esfera eterna». Se lee:
harto de los versos homéricos que recitaban de ciudad en ciudad, fustigó a los poetas que atribuyeron rasgos antropomórficos a los dioses y propuso a los griegos un solo Dios, que era, como una esfera eterna.
En este sentido, Platón, en el Timeo, afirma que la esfera es la figura más perfecta y más uniforme, dado que todos los puntos de la superficie equidistan del centro. Varios académicos de la posteridad han interpretado las expresiones de Jenófanes como esencialmente analógicas, en el sentido que el Dios propuesto era «esferoide», dado que esta forma es la menos imperfecta para representar a la divinidad. Este pensamiento se ve reflejado, décadas después, en Parménides, quien apunta: «el ser es semejante a la masa de una esfera bien redondeada, cuya fuerza es constante desde el centro, en cualquier dirección».
También el siciliano Empédocles de Agrigento integró los cuatro elementos fundamentales, tierra, agua, aire y fuego, en su cosmogonía radical, en una esfera. En uno de sus escritos, explica: «el sphairos redondo, que exulta en su soledad circular». Esta búsqueda de la forma como expresión del sustrato esencial resulta fundamental, pues, por ejemplo, los elementos básicos citados fueron asociados a ciertos cuerpos platónicos, esto es, a poliedros regulares específicos, como apuntamos en «La quinta esencia».
Al fondo de las consideraciones, las objeciones y los ataques de los filósofos iban dirigidos en contra de esas concepciones de los dioses como demasiado humanos. Por ejemplo, Jenófanes criticó fuertemente cómo los dioses fueron rebajados o reducidos a ficciones poéticas o a demonios. La búsqueda de algo más abstracto y permanente implicó un arduo trabajo en la Antigüedad, y esta inmutabilidad o permanencia se planteó desde algunos objetos matemáticos específicos, lo que también se descubre como herencia de la escuela de Pitágoras.
La tradición atribuye a los escritos de Hermes Trismegisto, un personaje helenístico legendario, producto del sincretismo entre Egipto y Grecia, la frase de nuestro epígrafe: «esa esfera intelectual, cuyo centro está en todas partes y la circunferencia en ninguna, que llamamos Dios». En suma, que la frase tiene su historia propia, llegando a la mente medieval en distintas versiones, ya entremezcladas con citas tomadas de las escrituras bíblicas, como sucede con 1 Reyes, 8, 27, donde Salomón expresa: «El cielo, el cielo de los cielos, no te contiene».
A la altura del siglo XVII, tiempos post renacentistas, pareciera existir un acuerdo básico con respecto a la correcta interpretación de esta tradición «esférica», también asociada con la denominada geometría sagrada: «Dios está en cada una de sus criaturas, pero ninguna lo limita». Al menos, para el matemático citado, Pascal, desde la teología, esto parecía no dejar lugar para la duda. La metáfora geométrica de la esfera se presentaba como la mejor manera de imaginar el asunto. En este contexto, se lee:
En aquel siglo desanimado, el espacio absoluto, que había sido una liberación para Bruno, fue un laberinto y un abismo para Pascal. Éste aborrecía el universo y hubiera querido adorar a Dios, pero Dios, para él, era menos real que el aborrecido universo. Deploró que no hablara el firmamento, comparó nuestra vida con la de náufragos en una isla desierta. Sintió el peso incesante del mundo físico, sintió vértigo, miedo y soledad, y los puso en otras palabras: «La naturaleza es una esfera infinita, cuyo centro está en todas partes y la circunferencia en ninguna.»
Curiosamente, Borges, interpretando a Pascal, explica las tachaduras y vacilaciones que en el manuscrito del notable pensador francés se observan. Esto refiere a una tachadura específica en la que Pascal incurrió. Resulta que el matemático había anotado «effroyable», espantosa, lo cual procedió a tachar. Es decir, la frase original decía: «La naturaleza es una esfera espantosa, cuyo centro está en todas partes y la circunferencia en ninguna». Nótese la evolución de las ideas, que parten de los dioses y sus formas, para transformarse en el universo, del cual, Pascal, prefiere expresarse como «la naturaleza». En cualquiera de los casos, la evocación de la esfera va en la dirección planteada por Platón, de quien Arquímedes, nuestro elogiado, seguramente, tendría un amplio conocimiento.
Fuente de imágenes ::
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/Arqu%C3%Admedes#/media/File:Gerhard_Thieme_Archimedes.jpg
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: http://isabelpgarcia.blogspot.com/2017/05/cuerpos-geometricos-v.html
[ 3 ] Imagen editada por Vinicio Barrientos Carles :: http://calculo.cc/temas/temas_geometria/volumen/teoria/v_pris_cilindro.html
[ 4 ] Imagen editada por Vinicio Barrientos Carles :: http://www.mat.ucm.es/cosasmdg/cdsmdg/05edumat/geometriahoy/experimentosgeom/lamejor.htm
[ 5 ] Imagen editada por vbc :: https:/www.universoformulas.com/matematicas/geometria/volumen-cono/ + http:/www.mat.ucm.es/cosasmdg/cdsmdg/05edumat/geometriahoy/experimentosgeom/lamejor.htm
[ 6 + 7 ] Imágenes elaboradas
[ 8 + 10 ] Imágenes editadas por Vinicio Barrientos Carles ::
http://www.mat.ucm.es/cosasmdg/cdsmdg/05edumat/geometriahoy/experimentosgeom/lamejor.htm
[ 9 ] Imagen editada por Vinicio Barrientos Carles :: https://arquimedes.red/post/calculo-por-arquimedes-del-volumen-de-la-esfera
[ 11 ] Imagen editada por Vinicio Barrientos Carles :: http://3con14.com/tips/207-t-%C2%B7-cilindro-circunscrito.html








