Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
Un mundo finito solo puede soportar una población finita, por lo tanto, el crecimiento poblacional deberá eventualmente llegar a ser igual a cero.
James Garrett Hardin
En nuestro reciente artículo titulado «Modelos matemáticos», en estos Suplementos Culturales LaHora, mencionábamos al inicio a Thomas Robert Malthus, quien advertía del inminente desastre si la población humana continuaba creciendo en forma geométrica. El clérigo y erudito británico contrastaba dos modelos de crecimiento, el geométrico y el aritmético, cuyas representaciones gráficas son, respectivamente, una curva exponencial y una recta. El planteamiento resultó impactante, en aquella época y mucho tiempo después, pues quedaba claro que la gráfica exponencial, siempre curvada hacia arriba, superaría a la recta en determinado momento, sin importar la tasa de crecimiento geométrico de la que se tratara. Con un argumento geométrico matemático, se demostraba que los alimentos, los recursos, terminarían agotándose en algún momento de nuestro futuro.
Específicamente Malthus escribía, en su libro An essay on the principle of population, publicado originalmente en inglés en 1798, lo siguiente:
Cuando no lo impide ningún obstáculo, la población se va doblando cada cierto número de años, creciendo de período en período, en una progresión geométrica. Los medios de subsistencia, en las circunstancias más favorables, no se aumentan sino en una progresión aritmética […] Si aceptamos mis postulados, afirmo que el poder de la población es infinitamente mayor que el poder de la Tierra para producir subsistencia para el hombre.
En esta obra, una de las más leídas durante el siglo XIX, empero, se incurría en un error en el modelo matemático empleado, pues se partía de que el crecimiento geométrico planteado se mantendría ad infinitum, por lo que ninguna cota impediría su paulatino crecimiento, la imparable duplicación del monto acumulado. Esto significaba que la población humana continuaría creciendo sin límite, si no se controlaba, puesto que aumentaría indefinidamente como una progresión geométrica. En otras palabras, los recursos, que aumentan únicamente en progresión aritmética, mediante un ritmo aditivo, nunca alcanzarían o serían suficientes en un futuro suficientemente lejano. Todo esto, así como las descripciones analíticas planteadas en la obra pasaron a constituir lo que la posteridad denominó la catástrofe malthusiana.
En breve, la catástrofe consiste en las consecuencias directas derivadas de la afirmación que el crecimiento de la población humana, libre de contenciones, consistía en un crecimiento exponencial puro, de carácter geométrico, mientras que la producción de alimentos según su argumento, no podría superar nunca un crecimiento de tipo lineal, o, a lo sumo potencial. De esta guisa, puesto que la tasa de crecimiento de la población era más acelerada que la de alimentos, a partir de un cierto umbral de población, Malthus pronosticó que, indefectiblemente, habría una escasez generalizada de los alimentos y los recursos, a gran escala, lo que conllevaría a una gran hambruna, la cual calculó que se sucedería a finales del siglo XIX, específicamente, para la década de 1880.
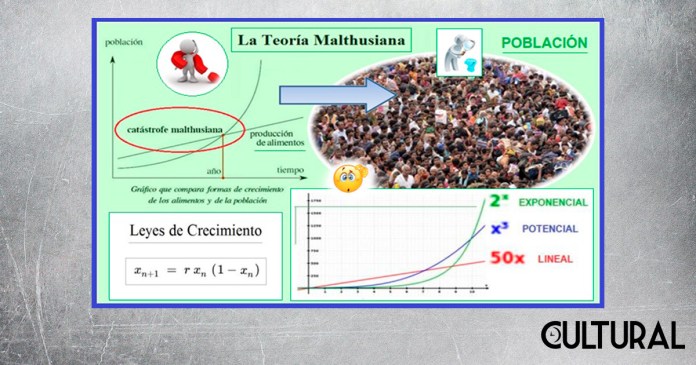
Por un lado, es un hecho que la gran hambruna predicha por Malthus jamás se produjo, mostrando que los presupuestos lógicos en el modelo matemático de Malthus eran simplistas y, en ocasiones, hasta erróneos. En efecto, Thomas Malthus era un demógrafo y economista político conservador, y es altamente probable que la catástrofe por él visionada se encontrara fuertemente influenciada por una visión pesimista del crecimiento poblacional, dejando de lado elementos clave en el modelo prescrito. También se ha dicho que la posición del teórico, como clérigo y religioso, sesgaban fuertemente sus opiniones respecto a la sexualidad y la reproducción. A pesar de ello, las tesis de Malthus, aunque resultaron desajustadas a los hechos, tuvieron una gran influencia política y social.
Los errores en los que incurrió Malthus son un ejemplo clásico de la mala adaptación de un determinado modelo matemático y los ajustes no tardaron en llegar. Pierre-François Verhulst fue un matemático belga, que publicó en 1838, 40 años después de la publicación del ensayo de Malthus, una obra que, basada en las estadísticas disponibles de aquel entonces, complementaba la teoría del crecimiento exponencial, o de la progresión geométrica, colocando un factor correctivo en la ecuación diferencial que anteriormente se estaba planteando. Hoy en día se le reconoce principalmente a Verhulst como el descubridor de la función logística, o curva sigmoidea, es decir, en forma de la letra S. Nuestro titular obedece a esta temática.
El nuevo modelo matemático de Verhulst para el crecimiento de una cierta población incorpora, básicamente, un elemento que contiene y expresa los factores que frenan el crecimiento sin límite. Históricamente dedicó los siguientes años a desarrollar el ajuste a la modelación, publicando su trabajo final en 1845. Más recientemente, el modelo logístico y algunas variantes han nuevamente acaparado la atención de académicos, desde los años 1970, y la teoría ha vuelto a recibir gran atención como un ejemplo importante de la teoría del caos, el determinismo y la dinámica de los sistemas complejos, posteriormente como una metodología estadística para la inferencia sobre sistemas sociales basados en datos discretos, especialmente útil en la nueva ciencia de datos, a través de la denominada regresión logística.
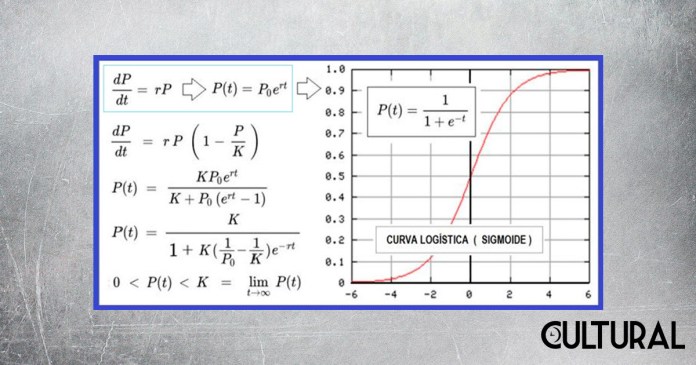
La idea fundamental del modelo logístico es colocar un factor que hace que la población se encuentre limitada por elementos o recursos determinados por el ambiente, que impiden que las poblaciones puedan seguir creciendo sin límite, colocando una cota superior para este crecimiento. Por ello se habla de un crecimiento acotado, es decir, limitado. En la imagen previa se observa la ecuación diferencial que plantea el modelo, así como la solución de tal condición de crecimiento, tanto en forma analítica, la función sigmoide, como en forma gráfica, la curva logística a la que en esta oportunidad nos estamos refiriendo.
En las ecuaciones previas puede observarse que la tasa de crecimiento r es común a ambos modelos, pero en el crecimiento sin límite esta tasa o razón de crecimiento afecta a la actual población P(t), mientras que en el modelo propuesto por Verhulst, el logístico, la tasa o razón afectará al producto de P(t) y a otro factor, constituido como [ K ─ P(t) ], lo que implica que cuando P(t) crezca, la tasa efectiva de crecimiento disminuirá, a tal punto que la población P(t) nunca podrá superar el valor K, al que efectivamente se le denominará capacidad de carga y representará un valor asintótico que el sistema, o el medio ambiente o entorno, impone a la dinámica poblacional.
Presentaremos, en lo que sigue, algunos ejemplos de las distintas aplicaciones y las ilustraciones que se tiene de este crecimiento acotado, que, aunque aparentemente más complejo, es de lo más natural posible. De hecho, faltó a Malthus una mirada detenida a su entorno natural para descubrir qué es lo que estaba erróneo en su planteamiento inicial. El crecimiento exponencial, sin límite, no se observa en ningún momento en la naturaleza, pues como dice el epígrafe, debido al ecólogo estadounidense, James Garrett Hardin, nada es finito en la naturaleza o en el mundo físico en el que existimos.
En forma sucinta, Hardin advirtió sobre los grandes peligros de la sobrepoblación, pero en una tónica y enfoque muy diferentes a los empleados por Malthus, más de siglo uy medio antes. Por otro lado, en resumen, el modelo logístico de crecimiento tiene una interpretación muy especial en la naturaleza y en los sistemas sociales, tales como la dinámica de las poblaciones de las distintas especies y su interacción con otras, como en el caso de los depredadores y las presas bajo ciertos supuestos que permiten la simplificación y el modelaje analítico, como hemos mencionado en nuestro artículo previo sobre los modelos matemáticos
Mientras, deseo regresar a la frase citada al inicio de esta primera parte del artículo, cuando Malthus anota: «… cuando no lo impide ningún obstáculo, la población se va doblando cada cierto número de años», trasladándola tal cual al ámbito financiero, pensando en que aquel que ha acumulado la suficiente riqueza para que su subsistencia ya no dependa de los réditos de su capital, tendríamos, si no se lo impide ningún obstáculo, un crecimiento geométrico que superaría a todos cuantos le rodean en una competencia fundada en unos principios erróneos de inequidad, basados en un simple, pero irreversible parámetro, el capital P(0) con el que por una u otra razón cuenta al inicio de la corrida del modelo.
Cabe decir que, lo anotado en el párrafo previo se cumplirá sí, y solo si, los supuestos del modelo de crecimiento no se modifican con unos elementos que impidan que el crecimiento responda a un modelo sin límite. Es primordial comprender cómo las cotas y los límites son requeridos y necesarios en cualquier fenómeno natural o social.
Sobre Malthus, se puede decir que ejerció una gran influencia en la economía política, siendo, a su vez, considerado el primer demógrafo de la Modernidad, pues sus ideas el revuelo que hemos mencionado. A pesar de sus sesgos, la llamada catástrofe malthusiana provocó, en los inicios del siglo XIX una serie de reacciones académicas respecto del crecimiento poblacional humano. Por primera vez se plantearon asuntos de carácter ético y científico al respecto de una posible sobrepoblación, lo que no dejaba de tener sus interesantes vertientes.
Miembro desde 1819 de la Real Sociedad (Royal Society of London for Improving Natural Knowledge), popularizó la teoría de la renta económica, aunque su fama se debe fundamentalmente al ensayo ya mencionado. Queremos insistir, en este primer segmento, que algunos detalles en el diseño de un determinado modelo se pueden transformar, prontamente, en los aspectos básicos que hagan que el mismo no trabaje correctamente, ejemplificando perfectamente, sobremanera, cómo los modelos matemáticos que no han sido ni adecuada ni pertinentemente contrastados con la evidencia empírica disponible suelen conducir al inescrutable error. El caso de la pandemia del Covid 19 sacó a relucir muchas de estas falencias.
Ahora, queremos citar cómo la curva logística que nos ocupa, a pesar de los formalismos matemáticos y las aparentes complicaciones analíticas, viene a ser un modelo al que la naturaleza suele recurrir más de lo que nos podemos imaginar. Como un primer ejemplo, debemos establecer que la reproducción de los seres vivos es un hecho inherentemente vinculado con la vida, a tal extremo que en la definición misma de un ser vivo se solía incluir el proceso de la reproducción como uno definitorio y esencial, es decir que, si nace, crece, se reproduce y muere, se trata entonces necesariamente de un ser vivo. Aunque esta definición ha quedado en simplista y obsoleta, he querido traerla a colación por el tema de la reproducción.
En efecto, existe un interesantísimo proceso biológico mediante el cual, dejando de lado los detalles técnicos, es factible la reproducción asexual de las células somáticas, a saber: el proceso de la mitosis, similar, pero diferente, al otro proceso de reproducción, la meiosis. En forma lacónica, la mitosis posibilita que una célula somática madre produzca dos células hijas, genéticamente idénticas, lo cual posibilita, a su vez, entre otras cosas, el crecimiento de los tejidos en los organismos pluricelulares, como nosotros los humanos, por ejemplo, la reparación tisular y la perduración del organismo en un tiempo determinado, mediante la autopoiesis celular y la homeostasis cibernética en los organismos complejos.
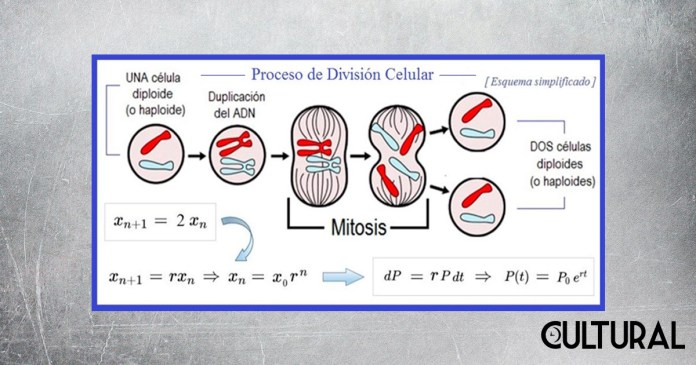
Piénsese entonces en una célula que se duplica en un cierto lapso y que sus descendientes continúan en esta duplicación tan formidable como maravillosa. Tomado en cuenta que las células no son eternas, lo cual es un fenómeno bioquímico per se, habrá que considerar la mortalidad de las más viejas. Aun así, la colección de células se incrementará a una determinada tasa de crecimiento, que permanecerá más o menos constante para la colectividad, y tendremos la duplicación a cada cierto intervalo de tiempo, que para simplificar podríamos considerar fijo y finito.
Al reflexionar sobre el asunto, podremos ver qué sucederá exactamente lo mismo en las poblaciones humanas, pues, aunque algunos tengan más hijos que otros, y muy seguramente algunos no tendrán descendencia, la colectividad tendrá una razón de crecimiento más o menos constante y podremos obtener así un determinado tiempo de duplicación. En este razonamiento Malthus estaba en lo correcto al plantear que, a una razón de crecimiento fija, el cambio en la población es proporcional a la población misma, de manera que un país diez veces más poblado tendrá un aumento poblacional diez veces mayor, una vez la tasa de crecimiento considerada sea la misma.
Lo anterior puede expresarse matemáticamente mediante la relación diferencial dada por dP = r P dt. Entonces, de tal ecuación se obtendrá por solución un crecimiento geométrico exponencial, y tal y como Malthus lo expresó, ninguna progresión de tipo aritmético podrá permanecer mayor que una de tipo geométrico, lo que temprano o tarde generará una crisis entre los recursos proporcionados por el ambiente y los medios de subsistencia y el tamaño que ha adquirido la población en cuestión.

En otras palabras, si se tiene que la tasa de crecimiento permanece constante, tendremos indefectiblemente un crecimiento geométrico del orden exponencial. En la naturaleza existen numerosos casos en los cuales este modelo de crecimiento se cumple, con una aproximación bastante grande. De hecho, las poblaciones animales, incluyendo las humanas, se comportarán de esta forma, así como lo hemos explicado en el caso de la mitosis celular. De hecho, existe una relación directa entre el tamaño de la colectividad, o del organismo, y la edad que los mismos tienen.
Un experimento clásico de laboratorio de biología elemental consiste en el cultivo de cierto microorganismo en un medio favorable, como una caja de Petri con agar u otro medio nutritivo, para estudiar precisamente su proliferación y crecimiento. Sin embargo, y aquí está el meollo de la limitación que debe ser introducida, la caja de Petri, que representa un mundo en pequeño, implica a su vez unas limitaciones bien definidas que el ambiente le impone al cultivo, influyendo notablemente en la dinámica reproductiva de la especie en estudio. Así, para nuestros propósitos de análisis, el modelo geométrico resultará insuficiente para explicar el fenómeno globalmente, es decir, en el largo plazo, funcionando únicamente de forma local, en el inicio del proceso de reproducción y crecimiento.
En efecto, el crecimiento no puede llevarse a cabo sin límite alguno, porque el mundo es finito y las dinámicas e interacciones medioambientales nunca están ausentes. Veamos otra ilustración del fenómeno que estamos explicando. Al observar la fecundación y el desarrollo subsecuente de un embrión humano, por ejemplo, puede verse cómo el óvulo fecundado comienza a subdividirse de manera tal que el número de células empieza a aumentar mediante la dinámica binaria antes descrita: 1, 2, 4, 8, 16, 32… y así sucesivamente.
De esta guisa se trata de un crecimiento exponencial, como en tantos otros casos que ilustran el fenómeno dictado por la mitosis. Sin embargo, y esto es muy importante, anótese que el feto en ciernes solo podrá crecer hasta un tamaño dado, determinado básicamente por el útero de la madre que le aloja, de forma que otros factores intervendrán disminuyendo de manera paulatina el incremento del número de células, y así la tasa de crecimiento se ralentizará disminuyendo conforme el feto se acerca al período del alumbramiento.
Después del tiempo usual para la especie, el bebé nacerá y continuará creciendo, ahora de manera totalmente independiente. Nuevamente se podrá observar acá un crecimiento que solo en períodos mostrará un ritmo geométrico, llegando finalmente a un número de células estable, al punto que la talla del individuo se volverá constante, hasta la senescencia, cuando la persona indefectiblemente fallecerá, justo cuando al organismo ya no le sea posible sostener sus procesos biológicos.
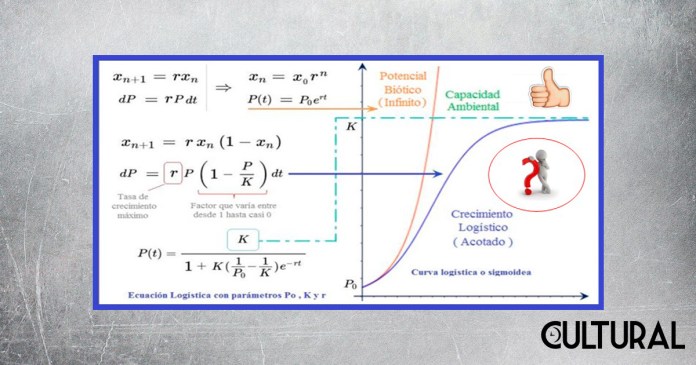
Como se mencionó anteriormente, fue el matemático belga P. F. Verhulst quien observó la situación de la imposibilidad de un crecimiento sin límite, porque implicaría que todo cuanto crece y se reproduce llegaría a límites sin cota, creciendo hasta el infinito matemático, cosa que empíricamente no era observable para ninguna especie. Es decir, Verhulst se vio en la necesidad de incluir un elemento en el modelo original de Malthus, un elemento tal que provocara la disminución del crecimiento conforme la población fuera creciendo, garantizando que nunca la población llegara a una cota K preestablecida, como se observa en la imagen.
En la continuidad de este artículo concluiremos al respecto de las profecías fallidas de Malthus y de cómo los datos y pronósticos actuales sobre el crecimiento poblacional humano se corresponden, en efecto, al crecimiento dictado por las ecuaciones diferenciales del modelo logístico descrito por una curva sigmoide que cumple ciertas características matemáticas.
Recapitulando, en el primer segmento presentamos las ideas revolucionarias del británico Thomas R. Malthus, de las cuales podía derivarse una catástrofe que sobrevendría al ser humano por una sobrepoblación inevitable, provocada por la progresión geométrica que gobierna su crecimiento poblacional. También se mencionaron los ajustes que unas décadas después introdujo el matemático belga P. F. Verhulst, quien consideró que existía un error fundamental en el modelo matemático que Malthus había utilizado.
En un momento posterior, hemos complementado con las bases biológicas por medio de las cuales el crecimiento exponencial es efectivamente el esperado, una vez se cumplan ciertas condiciones de bonanza biótica ambiental, mismas que usualmente se presentan al inicio del crecimiento de una determinada población. La adenda crucial que Verhulst incluyó en el modelo matemático para el crecimiento de una población, fue el límite que el medio ambiente proporciona, de forma natural, acotando el valor máximo que la población analizada puede asumir.
Lo anterior se debe, simplemente, a que el medio ambiente no podría soportar una población mayor a esta cota K preestablecida, a la cual se le denomina la capacidad de carga del sistema. Por ello, el modelo logístico que Verhulst introdujo por primera vez suele denominarse también modelo para el crecimiento acotado, el cual representa muy bien una gran cantidad de situaciones sociales y naturales de nuestra realidad factual. Véase la imagen que sigue.
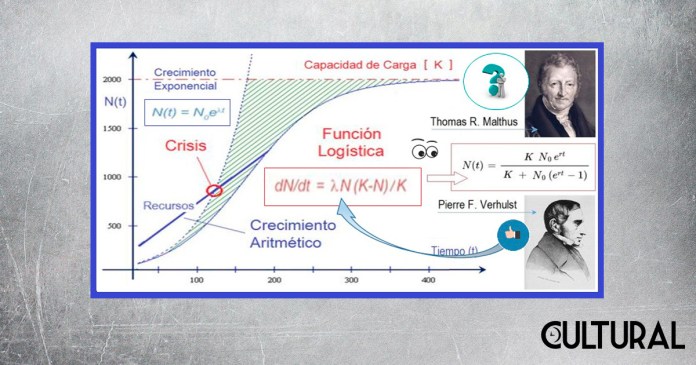
También hemos señalado que, aunque la gran hambruna que Malthus profetizó para 1880 nunca llegó, se presentaron repuntes de su visión apocalíptica, renovación conceptual que para inicios del siglo XX se adhirió a diversas formas políticas del pensamiento ultraconservador, tales como el fascismo, y otras de segregación racial fundamentalista, como el sionismo y el nazismo, las cuales propugnaron por un neomalthusianismo, caracterizado por ideas que propenden al exterminio masivo para permitir la supervivencia de unos pocos, los nobles, ante la amenaza de las masas pobres, que se reproducen a un ritmo mucho mayor que los pocos que viven con una adecuada calidad de vida.
Sin embargo de las ideas neomalthusianistas, las evidencias empíricas se han impuesto sobre las distintas teorías sociodemográficas, pues, al analizar las cifras de la población humana, podemos observar que los mejores modelos demográficos proyectan, para el final del siglo XXI, una estabilización del total de la población mundial, en alrededor de los 12 millardos de individuos, y lo que es relevante acá, con una evolución en el tiempo que valida el sigmoide predicho por el modelo de Verhulst, como puede apreciarse en la imagen que sigue.
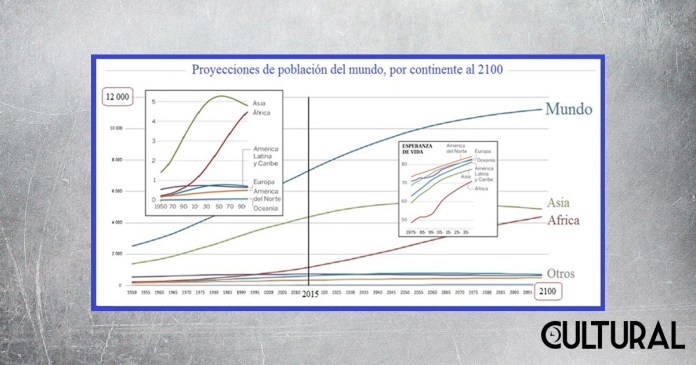
Verhulst era matemático de profesión y uno puede adivinar un abordaje un poco más objetivo del problema poblacional, sobre todo al reparar que Malthus se desempeñaba como clérigo anglicano, siendo altamente probable que haya asumido ciertos prejuicios que le interesaba popularizar. Si se toman literalmente ciertos versículos bíblicos, podría interpretarse que el ser humano es la creatura privilegiada de la creación, autovisualizándose como el propietario del mundo, para la particular satisfacción de sus intereses y en su propio beneficio. Antípoda será la postura que identifica a la especie humana como una más en la dinámica compleja que el planeta sostiene desde tiempos muy anteriores al aparecimiento del Homo sapiens.
Como estamos subrayando, Malthus defendió, a lo largo de su vida, una posición puritana respecto de la sexualidad humana y del crecimiento poblacional, proponiendo y predicando que, para solucionar el problema socioeconómico que sobrevendría por el exceso poblacional, se debía fortalecer la moral religiosa, implementando obstáculos represivos, de naturaleza sexual, como la castidad, el retraso del matrimonio y el celibato, evitando así que se presentaran otro tipo de obstáculos destructivos, como las hambrunas, las epidemias y las guerras, las que en última instancia debían ser interpretadas como correctivos divinos sobre los excesos provenientes de una naturaleza humana inherentemente pecadora.
Cuando se piensa que el ser humano es el amo del mundo, sin permitirse la comparación con otras especies emparentadas de animales cercanos y símiles, que han guardado un equilibrio bastante extendido a lo largo del tiempo, es posible sustraer del análisis otras posibles explicaciones respecto de los factores incidentes en la variación poblacional de una especie en general. Así, en contraposición de una visión antropocéntrica, existen abundantes evidencias empíricas que indican que el crecimiento de una cierta población siempre estará sometido a una serie de factores medioambientales que influyen determinantemente en su proliferación, factores tales como el alimento, el agua, los satisfactores del hábitat y otros elementos necesarios y disponibles en el ambiente donde la especie en cuestión se desarrolla.
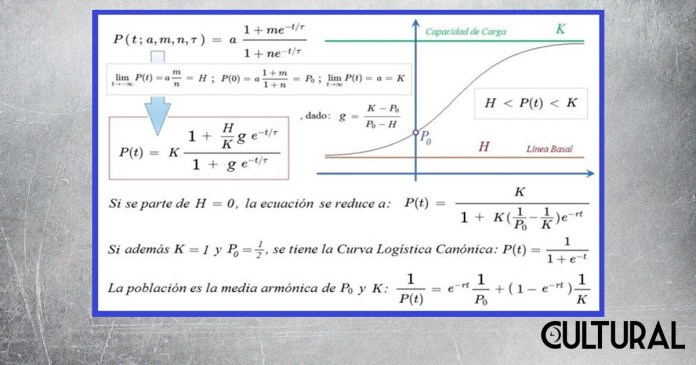
Justamente, en la biología de las poblaciones se define a la capacidad de carga del sistema como la carga máxima que el ambiente puede soportar con relación a una determinada especie, lo cual es ligeramente diferente del concepto de población en equilibrio.
En resumen, por debajo de la capacidad de carga, las poblaciones normalmente aumentarán, mientras que, por encima de la misma, disminuirán. Los factores que mantienen el tamaño de una población en equilibrio se conocen como factores reguladores o factores limitantes, los cuales pueden ser abióticos, tales como la falta de espacio, el suministro de alimentos o la cantidad de luz solar, o bióticos, como la competencia intraespecífica, la competencia interespecífica y las relaciones de depredación.
En este contexto, el difundido caso cinematográfico de los zombis apocalípticos, asesinos, que se hiperreproducen y que pueden vivir sin alimentos o recursos durante mucho tiempo, no puede sino ser un total absurdo científico. En la imagen se muestra una sigmoide con piso en H y capacidad de carga K, y se expresa al final un hecho matemáticamente relevante: la población en cualquier momento t es la media armónica entre la población inicial (Po) y la capacidad de carga (K), con ponderaciones complementarias en donde la correspondiente a Po decae exponencialmente.
Una primera conclusión en esta exposición es que la teoría del crecimiento exponencial es un modelo de crecimiento adecuado para poblaciones en condiciones de un potencial biótico suficiente, presentándose en variadas especies de insectos y pequeños organismos, así como en plantas, por su gran capacidad para autorregular su capacidad reproductiva. Aun así, se sabe que algunas especies, como la langosta migratoria, pueden derivar en plagas, que han llegado a superar los diez millardos de individuos. Un segundo corolario refiere a la limitación que presenta el modelo exponencial cuando la población crece mucho más allá de la población inicial Po, acercándose a la capacidad de carga K.
Nótese que el elemento K – P(t) en la ecuación diferencial introducida por Verhulst, hace casi dos siglos, servirá para atenuar la razón de crecimiento efectiva de la población, generando la curva sigmoidea que caracteriza y describe el modelo logístico que hemos presentado, estable_ciendo una asíntota que representa el equilibrio en el largo plazo. Sin embargo, es importante observar que ciertas variaciones en la dinámica del sistema podrían generar cambios caóticos que lleven a un nuevo estado estable, después de un interciclo en donde algunas especies pueden sucumbir y otras emerger.

Finalmente, vale señalar que la aplicación del concepto de la capacidad de carga para la población humana ha sido criticado por diversos autores, básicamente por no tomar en cuenta la magnitud de los intensos procesos antropogénicos, capaces de alterar la totalidad de las dinámicas medioambientales del planeta, vinculando una visión integral y holística que ciertos académicos han integrado en la denominada edad del Antropoceno. Esto, sin embargo, será temática para otra oportunidad, en la cual podremos describir cómo y por qué el mismo modelo logístico resulta demasiado simplista e insuficiente, cuando se trata de una adecuada descripción para un sistema de complejidad creciente, como lo es la humanidad.
Fuente de imágenes ::
[ 1 ] Imagen editada, Vinicio Barrientos Carles :: https://m.forocoches.com/foro/showthread.php?t=6430837 + https://elpais.com/internacional/2015/07/29/actualidad/1438196192_156373.html
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/Crecimiento_exponencial
[ 3 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/Mitosis#/media/File:%C3%89v%C3%A9nements_majeurs_de_la_Mitose_es.png
[ 5 ] Imagen editada por Vinicio Barrientos Carles :: http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/1750/1998/html/4_la_funcin_logstica.html
[ 4 + 6 + 7 + 8 ] Imágenes elaboradas por Vinicio Barrientos Carles
[ 9 ] Imagen editada por Vinicio Barrientos Carles :: https://lahora.gt/lh-suplementos-culturales/culturalahora/2023/08/26/modelos-matematicos/








