Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
La incertidumbre es una posición incómoda, pero la certeza es una posición absurda.
Voltaire
En 1798 Thomas R. Malthus publicó la primera edición de su obra An Essay on the Principle of Population. Allí puede leerse lo siguiente: «Cuando no lo impide ningún obstáculo, la población se va doblando cada cierto número de años, creciendo de período en período, en una progresión geométrica. Los medios de subsistencia, en las circunstancias más favorables, no se aumentan sino en una progresión aritmética».
Dos conceptos se contraponen en la cita previa: progresión aritmética versus progresión geométrica. La diferencia entre estos dos modelos de crecimiento radica en que en uno se desarrolla aplicando un sumando constante a cada miembro de la progresión, mientras que el otro crecerá aplicando un factor fijo a cada término, como el caso que plantea Malthus, cuando una duplicación cada cierto período se lleva a cabo. La cita del famoso demógrafo refiere a un crecimiento aritmético para los alimentos y recursos mientras que se tiene un crecimiento geométrico para la población.
La secuencia natural 1, 2, 3… es por ende una sucesión aritmética, pues cada término de la sucesión se encuentra sumando uno al término precedente. Otra sucesión aritmética, creciente, podría ser: 8, 11, 14, 17, 20, etcétera, en cuyo caso la diferencia constante observada es 3. Por otro lado, una secuencia geométrica de razón 2 sería: 3, 6, 12, 24, 48, etcétera. Puede observarse que la razón constante es el factor que se aplica de manera fija, y como se verifica en el ejemplo de la secuencia dada, cada término es el doble del valor del término que le antecede. La idea principal es que el crecimiento de una secuencia multiplicativa o geométrica es, con mucho, superior a un crecimiento de tipo aritmético.
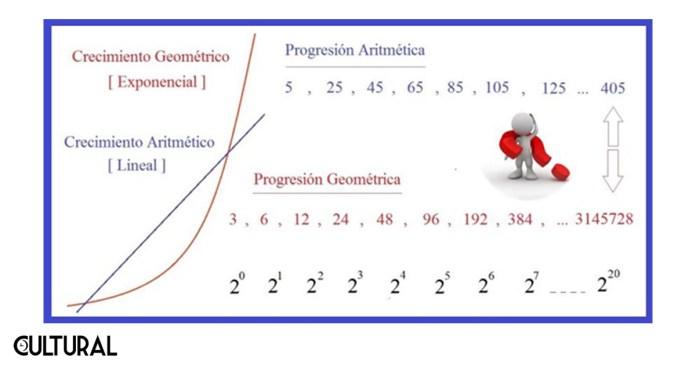
En la afamada predicción, del clérigo anglicano Malthus, denominada catástrofe malthusiana, está implícito el hecho matemático que, sin importar de cuáles secuencias se trate, dadas dos progresiones crecientes, una aritmética y otra geométrica, siempre será la segunda la que en algún momento supere a la primera. En lenguaje moderno, una exponencial siempre superará a cualquier recta en el plano, a partir de algún valor del tiempo en el eje de las abscisas.
El término geométrico no proviene ni debe relacionarse con el concepto de geometría como estudio de figuras y cuerpos, sino con otro concepto vinculado: el de multiplicación. Lo que sucede es que en el estudio de la proporcionalidad que se da en los triángulos, se utiliza repetidamente el concepto de razón, como cociente, y de esta forma aparecen factores fijos o constantes. En el caso de una secuencia, sucesión o progresión geométrica, en la que cada término se obtiene multiplicando por un factor constante, el uso del concepto geométrico resulta apropiado, por antonomasia y por la relación con las proporcionalidades prescritas.
Derivado de este concepto del tipo de sucesión y de crecimiento, existen numerosas aplicaciones, y una de ellas es la construcción de escalas. Una escala aritmética es aquella que presenta una sucesión aritmética, es la escala que utilizamos frecuentemente y de manera estándar. No obstante, cuando se está ante fenómenos que abarcan una gran variación, las escalas aritméticas suelen no ser tan útiles.
Por ejemplo, nuestra vista permite ubicar objetos a varios metros de distancia, quizá cientos, pero no así en distancias mucho mayores, para las cuales deberemos utilizar un catalejo o un telescopio. De igual manera, el sentido de la vista no puede auxiliarnos con magnitudes demasiado pequeñas. En general, nuestros sentidos y nuestras referencias sensibles son de tipo aritmético o lineal.
De esta guisa, en el mundo sensible, es decir, en el correspondiente a las percepciones desde los sentidos físicos, sea cual sea la naturaleza de una determinada especie, el uso de una escala aritmética es lo pertinente, en función de la movilidad y la mecánica que todos los seres vivos manifiestan. Sin embargo, para objetivos abstractos, analíticos, hemos hablado del micro, meso y macro mundo, lo que implica una diversidad mucho mayor en el tamaño de las cantidades que se registran. En este caso, la identificación del orden de magnitud viene dado por un exponente, y no es posible abarcar todos estos niveles en una única escala de tipo aritmético o usual.
Por lo anterior, una aplicación de las escalas de tipo geométrico es requerida, justamente cuando se necesita un alcance dado dentro de un gran recorrido de variación. Por ello los científicos han inventado prefijos para las unidades de medición, y estos prefijos de sistema internacional están en sí mismos en una progresión geométrica, de razón mil. Cuando se aplica el principio de crecimiento geométrico tendremos una escala geométrica. La imagen siguiente muestra tres tipos de escalas.
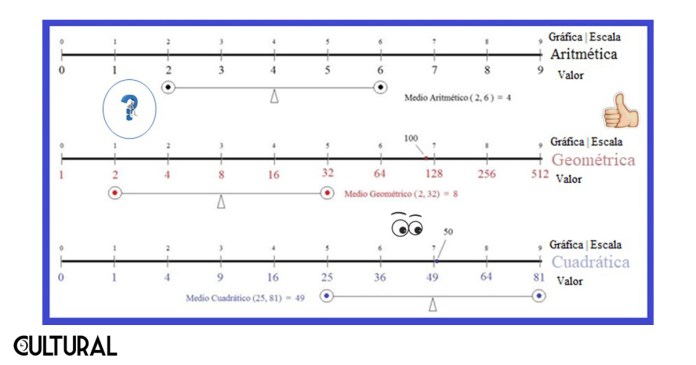
En la imagen previa, así como en otras que acompañan esta publicación, se incluyó una escala aritmética típica, varias escalas geométricas y una cuadrática. Como curiosidad, también se colocó un ejemplo de los llamados medios aritméticos, geométricos u otros, por estar posicionados al centro de los valores en cuestión, de forma equidistante, en las escalas correspondientes. Véase el artículo «Las medias pitagóricas» en esta sección de los Suplementos Culturales LaHora.
Es importante observar que el número de cifras que utiliza un número estará relacionado con el orden de magnitud de este número, es decir, con el exponente de la potencia más grande involucrada. En una secuencia geométrica, cada término sucesivo tendrá una cifra más cuando se escribe en el sistema de numeración correspondiente.
Por ejemplo, en el sistema decimal, un número entero de tres cifras estará acotado superiormente por 103, mientras que un número de 17 cifras lo estará por 1017. De manera similar, en el sistema binario, o de base 2, un número de cinco cifras, o cinco bits, estará acotado superiormente por 25 = 32, mientras otro número con 10 bits será inferior a 210 = 1024, pero mayor a 29 = 512 del sistema decimal.
Aquí aparece el concepto de logaritmo, que no es nada más que el exponente de un determinado número en una determinada base, y tendrá valor un poco debajo de la cantidad de cifras que el número posee, en el sistema de numeración dado. Así, el logaritmo de 1 000, en la base 10, es 3, puesto que 103 = 1 000. En base dos, o cualquier otra, es lo mismo. El logaritmo de 32 en la base 2 es igual a 5, pues 25 = 32.
De similar manera, un número de tres cifras (728 digamos) tendrá un logaritmo de base diez de «dos punto algo» (ie. log 728 = 2.9, aproximadamente), pues tendrá que ser un poco inferior a tres. En forma análoga, un número escrito con siete bits (10110112 digamos) tendrá un logaritmo de base dos de «seis punto algo» para que sea un poco menor a siete. En efecto: log2 (10110112) = log (91) / log (2) ≃ 6.5.
Ahora, como ejercicio, puedes buscar en tu calculador las dos funciones, exponencial (10x) y logaritmo (log), para posteriormente verificar que, si colocas un número cualquiera, puedes sacar su logaritmo exacto, para después, a esta respuesta, aplicarle el exponencial de base diez (10x), función a la cual antiguamente se le llamaba antilogaritmo. Estas dos funciones te permiten ir de una escala aritmética a otra geométrica, y viceversa. En general, en una base b (entero positivo), las funciones, exponencial de base b y logaritmo de base b, te posibilitan ir de una escala a la otra, y de alguna forma esta escala base b está relacionada con el sistema de numeración de la base b.
Cerramos con la célebre leyenda de Sisa, que habla sobre la invención del juego de ajedrez. El rey, complacido con el obsequio de tan novedoso e inteligente juego, quiso premiar a su creador y, ofreciéndole un gran palacio, el eximio y humilde inventor rechazó amablemente tan magnánima oferta. El rey, insistente y persuasivo, le pidió, casi en calidad de ruego, que le propusiera una recompensa. El inventor cedió, pidiéndole que le concediera arroz para su comarca, pidiéndole un grano por la primera casilla del tablero, dos para la segunda, cuatro para la tercera, y así sucesivamente duplicando la cantidad de arroz para cada una de las siguientes casillas.
Resultó que, después de que el rey ordenara que se le cumpliera tan peculiar pedido, los calculistas y guardas de los almacenes del reino tuvieron que informarle que ningún reino de este mundo podría cumplir tal solicitud. En efecto, la última casilla constaría de 263 granitos de arroz, y el total estaría cercano a 264 ≃1019 granos que equivale a 20 000 años de la producción actual de arroz en todo el mundo. Se cuenta que el rey quedó más que atónito ante lo que había sido, no cabe duda, un artilugio aritmético más del eximio matemático, inventor de tan agradable juego.
En suma, este ejemplo en la leyenda ilustra muy bien la falta de percepción que, muchas veces, tenemos respecto del llamado crecimiento exponencial, el que relaciona lo aritmético con lo geométrico, pues mientras las casillas avanzan aritméticamente de 1 en 1, los granos de arroz siguen una progresión geométrica de razón dos, misma que en algún momento desaparecerá de cualquier escala aritmética, por grande que la podamos proponer. Por otro lado, en paralelo, hemos esbozado la importancia y relación que tienen los modelos exponenciales y logarítmicos, que junto con los aritméticos constituyen los modelos matemáticos elementales, los más básicos.
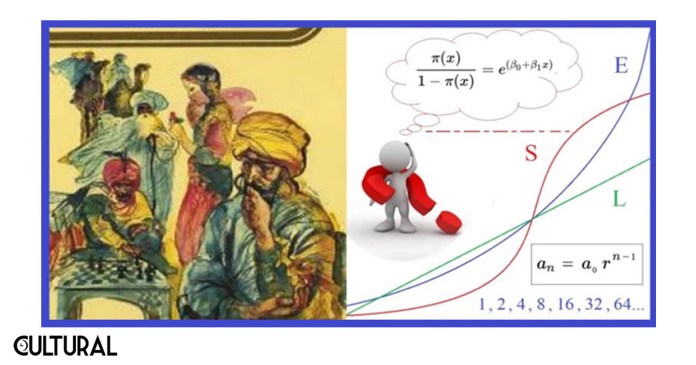
Pues bien, ya hemos presentado la diferencia existente entre una sucesión o progresión aritmética y otra de tipo geométrico, poniendo en evidencia el acelerado crecimiento que tiene la segunda respecto de la primera. Por ello citábamos la famosa catástrofe maltusiana. Fundamentalmente, mientras una secuencia aritmética crece mediante adición, una secuencia geométrica crece mediante multiplicación, lo que deriva en un crecimiento esencialmente mayor, siempre que la razón sea superior a uno (r > 1). Aunque esta distinción es cualitativamente sencilla de comprender, en términos cuantitativos siempre resulta sorprendente.
Es el caso de la leyenda de Lahur Sissa, quien, en premio de su loable invención del juego de ajedrez, pidió una recompensa consistente en un lote de trigo, que contuviera el monto de granos equivalente a un proceso sencillo que, descrito en términos actuales, implica una progresión geométrica. Para ilustrar la sorpresa ante tan magnánimo crecimiento, haremos un símil de la historia de Sissa, con alguna leve variación, para revisar nuestra intuición al respecto del crecimiento exponencial que describe muchos fenómenos de nuestro ambiente social y natural. Cabe recordar como el profesor y escritor brasileño Julio Cesar de Mello e Souza, mejor conocido por su seudónimo Malba Tahan, escribía en O Homem que Calculava:
Rey magnánimo –declaró el más sabio de los geómetras–: calculamos el número de granos de trigo solicitados por Sissa, y obtuvimos un número cuya magnitud resulta inconcebible para la imaginación humana
Supóngase que la madre naturaleza hubiera dispuesto autogenerarse mediante un maravilloso proceso de duplicación en el tiempo, empezando por una partícula elemental, un protón, por ejemplo, que en el momento cero constituiría la totalidad del universo. Asumamos que, sin nadie comprender mucho el cómo ni el porqué, esta partícula se duplicara de forma instantánea un poco antes de finalizar el primer día, de manera que ya iniciado el segundo se tuviera en el universo dos partículas.
Resulta que, continuando con este increíble proceso de creación y multiplicación de cuanto existe, tendríamos que al final del segundo día, e inicio del tercero, el universo estaría constituido por cuatro partículas. De manera que, de continuar así, indefinidamente en el tiempo, día tras día, semana tras semana, mes tras mes, año tras año, duplicándose el número de partículas ad infinitum, si es que el infinito puede tener sentido en nuestro universo, que los físicos y cosmólogos actuales aseveran que es finito y acotado. La pregunta que uno podría hacerse, ante este crecimiento exponencial, es cuánto tendría que transcurrir para que el planeta Tierra estuviera completamente conformado, con toda la materia que hay en él.
De igual forma, preguntarse por cuánto tiempo se tomaría para que, la madre naturaleza, terminara de conformar el Sistema Solar, o nuestra galaxia, la Vía Láctea. Por un lado, este fenómeno de la duplicación no es algo tan fantástico como podríamos suponer, dado que varios fenómenos de tipo social o natural, tales como el crecimiento bacteriano, presentan el crecimiento exponencial. En efecto, la reproducción de bacterias está basada en fisión celular binaria, la cual suele sucederse ante las condiciones propicias para esta maravillosa duplicación, con la diferencia que el lapso en el que una bacteria se duplica, y con ello la población bacteriana completa, puede ser tan solo de algunos minutos.
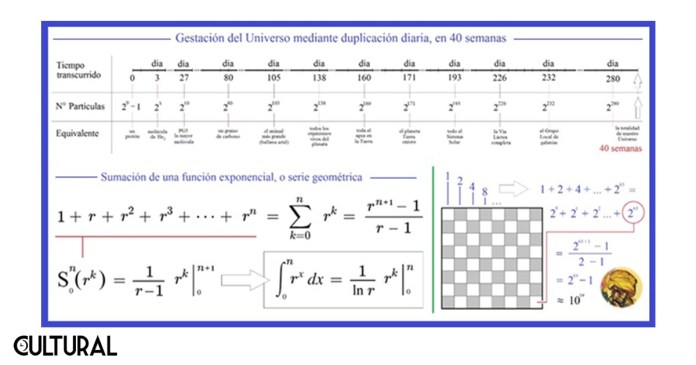
Pues bien, para la sorpresa de quien nos lee y plantee tales interrogantes, ante el hipotético planteamiento es que una duplicación diaria sostenida generaría toda la materia del universo completo en un tiempo equivalente a la duración del embarazo humano, es decir que bastarían tan solo 40 semanas para que toda partícula del universo estuviera generada antes de este tiempo, menor a un año. En términos formales, estaríamos tratando de una cantidad escrita con 280 bits, es decir, de un tamaño equivalente a 2280 ≃ 1085 partículas, un número que es posible escribir en cualquier calculador científico de bolsillo.
Nótese que, a diferencia del caso del tablero de ajedrez, acá no se suman las partículas del primer día con las del segundo, con las del tercero, lo cual en un crecimiento exponencial no es ciertamente crucial, pues en todo caso, discreto o continuo, la adición o integración de una función exponencial es a su vez una dependencia de tipo exponencial, como se ve en el caso de la suma en el tablero de ajedrez.
La razón por la cual la función exponencial, sea de crecimiento o decrecimiento, es tan importante en la modelación matemática es debido a una propiedad formal que la función cumple, causal de su aparecimiento, y que aparece en variados fenómenos, como el estudio de poblaciones, el decaimiento radioactivo y distintos fenómenos financieros. Una gran cantidad de hechos de la naturaleza, o de la sociedad humana, son explicados a través de las relaciones que existen entre las variables y sus tasas de cambio.
Un primer modelo, intuitivamente bastante claro, es aquel que tiene una tasa de variación constante, es decir, que varía uniformemente. Estos fenómenos responden a la proporcionalidad que vemos en las figuras geométricas, a través del concepto de la escala, y que modelan una secuencia aritmética. La función que modela un fenómeno de tasa constante es la función lineal, cuya gráfica es una línea recta. Es justamente el modelo del interés simple, que aplica un porcentaje fijo sobre el capital inicial. Las funciones lineales aparecen en muchos modelos de uso cotidiano, como el asunto de los costos a un precio fijo. Compras el doble o el triple, entonces pagas el doble o el triple. La tasa es fija.
Sin embargo, también estamos relacionados con el modelo del interés compuesto, el cual aplica una tasa fija, pero sobre la cantidad acumulada, es decir, sobre el monto actual y no sobre el capital inicial invertido, lo que significa que la tasa de crecimiento real es variable y proporcional a la cantidad existente, que es la misma relación que se presenta en el crecimiento de una cierta población, pues mientras más población, más será el número de nuevos elementos.
En la Matemática más avanzada, aparecen diversas estructuras del tipo exponencial, pues resuelven ecuaciones en donde las tasas de cambio son proporcionales al valor actual de la variable. Esto puede observarse en sistemas dinámicos complejos, dando lugar a soluciones análogas al caso de un crecimiento exponencial numérico. Posiblemente se piense que estos modelos son complicados, siendo la verdad lo totalmente opuesto. Por ejemplo, la derivación y la integración de funciones, objetos o sistemas de tipo exponencial son preferidas, por sencillas.
En términos generales, dos curvas tipo son relevantes en el modelaje de una serie de fenómenos; las lineales, relacionadas con la sucesión aritmética, y las exponenciales, correspondientes a la sucesión geométrica. Por ello, es importante distinguir entre fenómenos aditivos, computados por diferencias, y otros muy similares, de tipo multiplicativo, en donde las razones o cocientes son las herramientas adecuadas. Existe una correspondencia, homomorfismo, entre la adición en los números reales de una escala aritmética con la multiplicación en una escala geométrica de los números reales positivos.
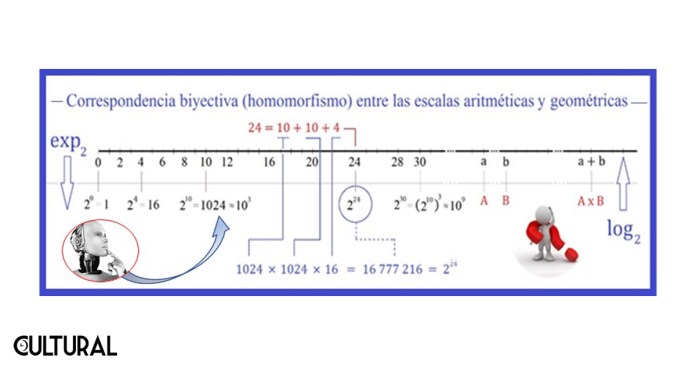
El crecimiento poblacional y el particular de los cálculos que deben realizarse en finanzas son una clara muestra de la significancia de la comprensión de posibles aplicaciones del modelo exponencial, y de ciertas nociones relacionadas, como la conversión entre una escala aritmética y una geométrica a través de la función logarítmica. El modelaje de relaciones y sistemas es un campo multidisciplinario que no es exclusivo de especialistas en Matemática, sino que por el contrario atañe a profesionales de varias áreas de estudio, sobre todo en lo que respecta al planteamiento de las condiciones que se requieren para delimitar los alcances y las fronteras del modelo.
Como se ha planteado, un modelo exponencial no puede ser sostenido en el tiempo, a menos que existan condicionantes que lo acoten, detalle que podremos abordar en un posterior acercamiento con el modelo de regresión logística y las funciones sigmoideas de modelación. Reza en el ideario popular un adagio que dice que las matemáticas no fallan, que los números no se equivocan. En varias publicaciones hemos defendido la idea que tales percepciones el quehacer matemático conllevan varios tipos de sesgo, fundamentalmente porque no promueven el análisis que debe ser realizado para la aplicación de algún modelo matemático, que siempre reviste consideraciones sobre las premisas que se asumen para su utilización.
Ante todo, es importante identificar en tales afirmaciones aspectos que pueden ser utilizados para invalidar modelos matemáticos inapropiados. En general, un modelo matemático puede fallar, no por los procesos formales en sí que en él se desarrollan, sino más bien porque para ser aplicados se necesita que ciertas condicionantes que se asumen se verifiquen, lo cual en ciertos casos del mundo factual no se da, siendo muchas veces situaciones contingentes, pero no necesarias.
Así, el meollo del asunto de la validez radica en las circunstancias y en posibles detalles específicos que se deben dar en la problemática que se aborda, y aunque es cierto que la Matemática es una ciencia formal, el mal uso o el abuso de un determinado modelo representa una falla humana mucho más frecuente de lo que uno pudiera imaginar. En este sentido, no es un hecho nuevo que existen numerosas advertencias al respecto del uso de los números para describir situaciones de la vida real.
Por ejemplo, para ilustrar las malas prácticas, recordar que hace ya 70 años que fue publicado Cómo mentir con estadísticas, un pequeño texto que en modo coloquial describe una diversidad de casos en los cuales se puede incurrir en el error al momento de interpretar las cantidades y lo que estas expresan. De forma específica, lo que el libro intenta comunicar es que en nombre de la fabulosa actividad matemática y de los resultados estadísticos más básicos suelen cometerse grandes abusos, de los cuales debemos estar siempre alertas.
Esto que se describe es similar al argumento ad hominem y otras falacias retóricas similares. No porque lo ha dicho una personalidad deberá ser una gran verdad o una dirección a seguir. De similar forma, no por citar notables hechos científicos o matemáticos se tendrá que someter el discurso a las supuestas consecuencias de los mismos, sin antes realizar una exhaustiva revisión sobre el uso y la pertinencia de la aparente aplicabilidad.
En breve, resumiendo los párrafos precedentes, podemos establecer que no porque se trate de un modelo matemático tiene este que estar bien construido, o se esté ante una correcta aplicación del mismo. Esto es particularmente útil cuando se habla de una determinada proyección, o una estimación, generalmente realizada por expertos. La citación de los peritos o el llamado a la fortaleza de las técnicas matemáticas empleadas no es para nada garantía de los resultados que se están defendiendo. Esto es muy importante para la evaluación técnica y científica de cualquier publicación. Se debe estar alerta ante estas situaciones.
En nuestro medio, el modelo de estimación lineal es ampliamente utilizado, por ser el más conocido en el ámbito de las ciencias económicas. Quizá podríamos decir que es sobre usado, esto es, que existe un abuso en su utilización. Lo que sucede es que, muchos fenómenos de nuestro entorno, sea social o natural, no se encuentran fundamentados, o correlacionados, con un modelo lineal, y este es un primer punto, importantísimo, que debe revisarse, puesto que en estos otros casos debe recurrirse al uso y aplicación de modelos matemáticos no lineales.
Conviene, a manera de ejemplo, citar un caso particular sobre esta situación, será interesante citar un caso real de nuestro contexto en Guatemala. Hace ya varios años, casi seis, trascendió que el jefe de la SAT, Juan Francisco Solórzano Foppa, fue destituido de su cargo por incumplimiento de una cláusula específica de su contrato, referida al monto de recaudación tributaria a la que se debería haber llegado. Llamó la atención la discusión que se generó en torno a la decisión finalmente adoptada.
El detalle es que la meta prevista para ese año ascendía a Q 57 463 millones, mientras que lo recaudado a la fecha de corte fue de Q 56 177 millones, equivalente a 97.8 % del total planteado. El modelo matemático interviene en lo que se refiere a un detalle que pasó casi desapercibido por los analistas, y es que la brecha fiscal establecida se situó en Q 166 millones faltantes. La razón de esto es que proyecciones y estimaciones que el equipo técnico realizó, con base en un modelo matemático económico-financiero, indicaron que era factible descontar un monto de Q 1 120 millones de la correspondiente meta de recaudación, que se trataba de un sesgo aceptable en el modelo.
Al realizar las restas se tuvo un remanente de 166 millones, entiéndase: 56 463 – 1 120 – 56 177 = 166, faltante. La discusión aquí oculta es: ¿qué bases y premisas en el modelo permitieron descontar Q 1 120 millones (2 % del monto original) pero no aceptaba un descuento de Q 1 286 millones (2.3 % del monto original)? Cuando se hace un análisis cuantitativo y gráfico de la situación, la pregunta del párrafo previo lleva a un cuestionamiento más profundo sobre los criterios empleados en la destitución del funcionario, estableciendo que no fueron verdaderamente de tipo técnico, sino más bien de otra naturaleza, como bien lo señalaron los distintos medios de comunicación en su momento.

En la imagen se han colocado dos pares de rectas. La gráfica a escala que muestra la base de estimación y la cantidad descargada de la meta de recaudación presupuestaria se encuentra abajo (flecha azul: gráfica a escala), pero, como se verá, no se logran distinguir las dos estimaciones, una en verde y otra en rojo. Por ello se ha multiplicado por diez la escala en las ordenadas (eje vertical), para que ambas estimaciones sean distinguibles. La estimación en rojo representa 2.3 % de dispensa en la recaudación, mientras que la estimación en verde corresponde únicamente con 2 %, que es lo que efectivamente se dispensó.
La objeción de tipo técnico es que un cambio en la pendiente, o proporción, a dispensar, no es substancialmente diferente entre un valor de 2 y otro de 2.3. En cuanto al ángulo de inclinación de las rectas proyectivas, tómese nota: diferencia de la inclinación (en escala aritmética estándar) entre la recta verde y la recta roja es de apenas 0.3°, lo que significa aproximadamente la 300-ésima parte de un ángulo recto. Esta diferencia en la inclinación entre ambas rectas equivale a la diferencia entre asumir un criterio de estimación, el verde asumido, y el otro, el rojo que era el que se necesita asumir para la no destitución.
Todo esto implica, en términos quizá más ligeros, que la aceptación de un sesgo de un 2 % conlleva, de manera natural, a la aceptación de un sesgo mayor, que podría llegar, inclusive, hasta 3 %. En la docimasia estadística es frecuente aprobar o desaprobar una conjetura respecto a algún parámetro poblacional. Se suele distinguir entre una significancia fuerte (con α = 1 %) versus una docimasia débil (con α = 5 %).
Acá es claro que la aceptación de un 2 % de dispensa en la recaudación, pero el rechazo de otra de 2.3 %, no puede responder a criterios técnicos dentro de cualquiera que sea el modelo que se utilizó. Aun así, curiosamente, ninguno de los comentaristas o analistas preguntó sobre cuál fue el modelo de estimación con el que se determinó que una dispensa de Q 1 200 millones era aceptable, pero no sobre una cantidad superior en Q 166 millones, cuando, como se ha establecido, representa una estimación del 2 % sobre la base, considerada aceptable, pero no así otra que ascienda a 2.3 %.
Recapitulando, lo más relevante del caso presentado es concluir sobre cuán importante resulta analizar cómo operan exactamente los modelos matemáticos, no asumiendo en ningún momento una validez universal, puesto que aun las complejidades más grandes pueden ser reducidas a explicaciones comprensibles, en miras a evaluar desde otros ángulos el correspondiente uso, y establecer si la aplicación del modelo prospectivo es factible, o si, por el contrario, consistirá en un abuso o subterfugio tendiente a ocultar una manipulación que subyace debajo de engañosos tecnicismos. Esto último suele utilizarse frecuentemente. Ahí la importancia de la participación de profesionales calificados.
En este segmento final, deseo traer a colación un ejemplo de aplicación de los modelos matemáticos, pero especialmente uno tomado del contexto del mundo natural, en donde las decisiones humanas muchas veces no llegan a alterar el orden existente en la naturaleza. El caso es conocido como el modelo de depredadores y presas. Para ello empezar citando al escritor Herbert George Wells, quien dijo: «Adaptarse o perecer, ahora como siempre, es el imperativo inexorable de la naturaleza».
Se lee que Wells tuvo una infancia y juventud difíciles, y aunque ganó una beca para estudiar biología, terminó obteniendo el grado en zoología. Por ello no es extraño que una de sus frases célebres exprese el imperativo inexorable que él visualiza en la naturaleza: adaptarse o perecer. Su idea al respecto de la interacción de las especies aparece en varias de sus obras, como es el caso de su clásico La guerra de los mundos (1898) o la misma La máquina el tiempo (1895). En estos albores del siglo XX no se tenía la claridad que ahora tenemos respecto de nuestra presencia como especie trágicamente determinante del futuro del planeta, en cuanto a la biota y los ecosistemas.
En cierta ocasión, tuve la oportunidad de ver un programa interesantísimo, en alguno de los canales culturales e informativos de televisión por cable, en el cual se mostraban los detalles y la evolución de un proyecto orientado a medir el origen de las variaciones cuantitativas en una determinada población de ñúes azules, durante un ciclo anual en el que se efectúan procesos de movilización y migración, circunvalando cierta región en los alrededores del lago Victoria, en el Parque nacional del Serengueti de la República de Tanzania, África.
Pues bien, el caso es que la comunidad de ñúes estudiada en el Serengueti demostró que la población total se mantenía en el ciclo anual, lo que viene a reforzar los conceptos clave relacionados con el balance de la naturaleza. La hipótesis de que los sistemas ecológicos tienden a un equilibrio estable por medio de la homeostasis, se demuestra, pero, en particular, evidenciando que pequeños cambios en las variables del sistema serán corregidos por retroalimentación negativa, con la que se regresará a los valores de la variable en su punto de equilibrio original. Existen modelos matemáticos muy refinados que confirman y explican las hipótesis referidas al funcionamiento de ecosistemas complejos como este que estamos citando.
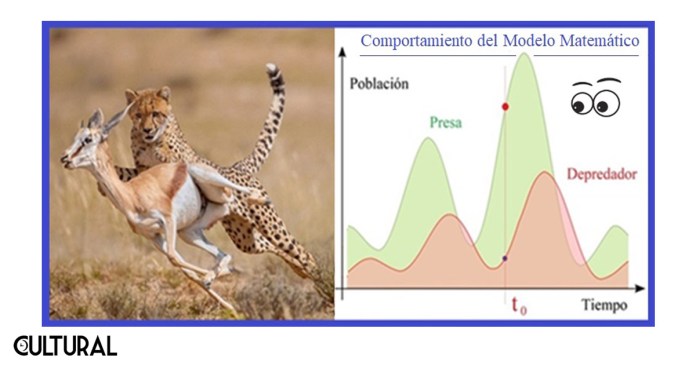
Empero, en sistemas mucho más sencillos, en donde los modelos deterministas pueden funcionar eficientemente dentro de un entorno temporal suficientemente corto, los conceptos del equilibrio ecológico resultan increíblemente adecuados. Específicamente, los trabajos de investigación en esta disciplina se diferencian con respecto de la mayoría de los trabajos en las demás ramas de la Biología, por el mayor uso de herramientas analíticas, tales como la estadística y los modelos matemáticos, deterministas o estocásticos. Pioneros sobre el uso de los modelos matemáticos para describir las dinámicas de sistemas biológicos fueron, de manera casi simultánea, pero de forma independiente, los matemáticos y físicos Alfred J. Lotka en 1925 y Vito Volterra en 1926, al plantear las ecuaciones de Lotka─Volterra, o ecuaciones de presa─depredador.
El modelo Lotka-Volterra, en su forma más simple, trata con dos tipos de especies diferentes pero unidas por un fuerte vínculo enmarcado en el más puro darwinismo: una especie presa (focas, conejos, gacelas, babuinos) y otra especie depredadora (tiburones, zorros, guepardos, leopardos) que comparten un mismo ecosistema. Las premisas sobre el modelo biológico son igualmente simples, a saber:
- la especie presa se desenvuelve en un medio sin escasez de alimento y que la especie presa no tiene otro predador adicional al declarado en el modelo
- la especie predadora únicamente consume la especie presa declarada en el modelo y ninguna otra, es decir, existe únicamente competencia interespecífica.
Entonces las ecuaciones del modelo son un par de ecuaciones diferenciales no lineales de primer orden que se usan para describir las dinámicas de la interacción, de donde es posible obtener las variaciones de las poblaciones de ambas especies. La matematización en el proceso constitutivo de la ecología fue una apertura a nuevos métodos de abordaje de los problemas en biología y, aún en la actualidad, se continúa desarrollando esta metodología, con herramientas cada vez más potentes. Una primera gran conclusión del modelo matemático es que predice ciclos y períodos para las poblaciones que inicialmente se colocan en la dinámica de interacción.
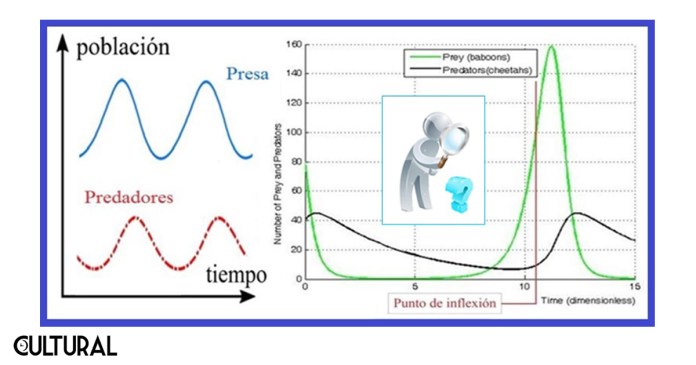
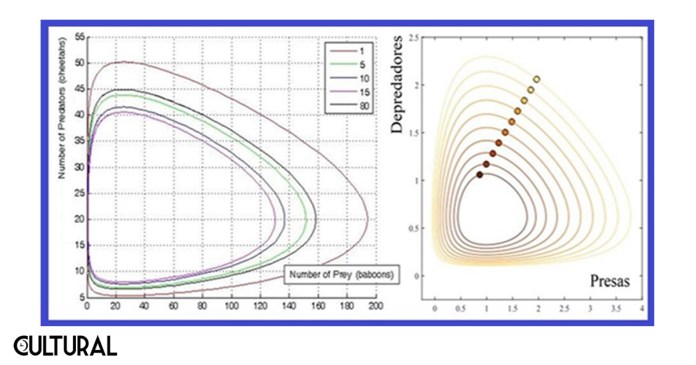
Otro aspecto que es posible concluir, que introduce el concepto del atractor del ciclo límite, puede describirse a través de la gráfica de fase, cuando se plotean los puntos de las parejas poblacionales, presa─depredador, mostrando ciclos cerrados que son recorridos en un sentido o el otro. El hecho de que las trayectorias tenderán a una curva límite si se somete el sistema a pequeñas variaciones será una idea generadora dentro de la nueva concepción de un caos determinístico, el cual se presenta cuando en el modelo intervienen otros parámetros aparte de los propios que describen a las dos especies en cuestión.
Esto resultará muy importante, pues un ecosistema con una o dos especies no deja de ser una hermosa abstracción, pero en términos factuales, una tremenda idealización muy lejana a la realidad física de la naturaleza. Los conceptos del paradigma de la complejidad y la teoría del caos, especialmente la no linealidad, son esenciales en el abordaje teórico de estos tópicos.
En breve, hace menos de un siglo que las ecuaciones de Lotka─Volterra aparecieron en el concierto de las nuevas ciencias biológicas, y desde entonces hemos recorrido una larga trayectoria, y seguimos moviéndonos hacia una mejor comprensión de nuestro mundo natural. Aunque el concepto de equilibrio en la naturaleza una vez gobernó la investigación ecológica, influyendo en las políticas de gestión de los recursos naturales y fortaleciendo algunas posturas conservacionistas radicales que predicaron que la intervención humana era inaceptable.
Esta no intervención del ser humano ha pasado a ser una de las claves primordiales para la conservación del equilibrio en todo el planeta. De diversas maneras, de una forma apriorística, el hecho es que vale la pena profundizar en las modificaciones más recientes de la evolución del pensamiento ecológico, pues en este siglo XXI deberemos asumir las estrategias correctas respecto a nuestro mundo, y para ello nuestra ignorancia o nuestro saber podrían ser el factor determinante para la supervivencia de tantas especies, incluida la nuestra. Por ello hemos querido colocar este ejemplo al respecto de la comprensión del intrincado equilibrio de los ecosistemas.
En fin, hemos presentado un boceto de las ideas fundamentales en torno de los conceptos y las aplicaciones de los modelos matemáticos. Daremos continuidad, tratando el caso particular de los modelos epidemiológicos analíticos, los cuales adquirieron notable importancia en la reciente pandemia del Covid 19, cuando muchos y muchas escucharon por primera vez al respecto. La curva logística y similares son producto de esta clase de modelos, que, como veremos, aparecen con frecuencia en los fenómenos naturales. Como epílogo, comprender que todos estos modelos matemáticos, más complejos, son, en su base, una combinación de secuencias aritméticas y geométricas, es decir, una combinación de funciones lineales y exponenciales. Así que tomemos esta publicación como el primer capítulo del texto.
Fuente de imágenes ::
[ 1 + 2 + 3 + 4 + 5 + 7 ] Imágenes elaboradas por el autor, Vinicio Barrientos Carles
[ 6 ] Imagen editada por vbc :: http://www.vc.ehu.es/campus/centros/farmacia/deptos-f/depme/apuntes/gracia/2003-2004/AmplMate/modelos1.htm
[ 8 ] Imagen editada por Vinicio Barrientos Carles :: https://gazetagt.com/presas-y-depredadores/
[ 9 + 10 ] Imagen editada por vbc :: https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations








