Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
No podemos enseñar nada a nadie. Tan solo podemos ayudar a que descubran por sí mismos.
Galileo Galilei
Hace ya más de dos meses que escribí unos artículos, solicitando ayuda financiera para que el equipo matemático olímpico guatemalteco pudiera viajar a Japón, a la Olimpíada Internacional de Matemática –IMO 2023–, por sus siglas en inglés, International Mathematical Olympiad. Aunque la ayuda financiera empezó a llegar, para costear el viaje de ida y vuelta, comentamos, en esa oportunidad, que Luis von Ahn decidió apoyar de tajo el requerimiento de estos fondos, por lo que continuamos agradecidos por su loable acción. Aprovechamos para comentar lo lamentable que resulta que el Estado de Guatemala no apoye este tipo de eventos, lo cual refleja nuestra pobre concepción del desarrollo y del mismo futuro que estamos construyendo.
Las protagonistas del torneo, representantes de Guatemala en el torneo, arribaron a Japón el pasado domingo 2 de julio, en compañía del tutor asignado que las acompaña, en calidad de coordinador del equipo olímpico guatemalteco. El evento se llevará a cabo en la ciudad japonesa de Chiba, entre el domingo recién pasado y el jueves 13 de julio de los corrientes. Sobre la IMO, Wikipedia dice «es una competencia anual de matemáticas para estudiantes preuniversitarios y es la más antigua de las Olimpiadas Internacionales de Ciencias». La antigüedad se remonta al año de 1959, en Rumania, de manera tal que esta IMO 2023 es la 64.ª edición del prestigioso evento, dirigido a jóvenes talentosos de todo el mundo.
Se trata de las jóvenes Arianée Abigail Enríquez Contreras, Aby, de 17 años y Ana Julia Rojas Buezo, Ana Julia, de 16 años, ganadoras de los torneos matemáticos a nivel nacional. En estos momentos, cuando se publica esta nota, es posible que Aby y Ana Julia ya hayan realizado sus respectivas participaciones en el prestigioso evento. Aunque previamente han participado en competencias de nivel internacional, ganando algunas preseas, para Aby y Ana Julia esta será su primera experiencia en una IMO, la competencia mundial de mayor cobertura y, por ende, de mayor dificultad.
Con relación al evento, más de un ciento de países participan, año con año en la IMO. La página oficial es Olimpíada Internacional de Matemática, siendo la correspondiente a la IMO 2023 la ubicada en este enlace. Cada país participante puede enviar un equipo de un máximo de seis estudiantes, menores de 20 años, que no hayan ingresado a sus estudios universitarios, es decir, que estén cursando su secundaria, no existiendo límite inferior para la edad de inclusión. Esto último implica que un joven de 12 años podría participar, aunque lo usual son competidores y competidoras adolescentes. También puede integrar el equipo un líder y un tutor, colíder, y algunos observadores. Al menos un adulto debe acompañar a los menores.

Es importante reparar que existen varias olimpíadas matemáticas, de acuerdo a la región que cubren. Derivado de este hecho, cabe señalar que se presentan distintos niveles de dificultad. La IMO, de la que ahora estamos conversando, es la que corresponde al nivel más alto, pues abarca a todo el mundo, pudiendo participar cualquier país que haya celebrado los procesos de eliminatoria a nivel nacional. Es muy similar a las olimpíadas deportivas que todos y todas conocemos. Así como en los deportes físicos, el equipo representante posee características idóneas para la competencia mundial, tanto por el talento innato como por el entrenamiento seguido para enfrentarse a sus congéneres a nivel global. Para describir rápidamente el evento, citamos nuevamente la Wikipedia:
La competición consta de dos cuestionarios con tres problemas cada uno. Cada pregunta da una puntuación máxima de 7 puntos, por lo que la puntuación máxima total es de 42 puntos. La prueba se desarrolla en dos días, en cada uno de los cuales el concursante dispone de cuatro horas y media para resolver tres problemas. Estos se escogen entre varias áreas de la matemática vista en secundaria, los cuales pueden clasificarse, grosso modo, en geometría, aritmética (teoría de números), álgebra y combinatoria. No se requieren conocimientos de matemáticas superiores y de las soluciones se espera que sean cortas y elegantes. Encontrarlas requiere, sin embargo, ingenio excepcional y habilidad matemática.
Sobre esto último, como hemos mencionado, estaremos ampliando con un posterior ejemplo. No obstante, para la inquietud natural de quien nos sigue, adelantándome en el camino esclarecedor sobre en qué consiste la competencia y a qué tipo de retos se podría enfrentar una competidora o un competidor olímpico, copio a continuación un problema ejemplo, tomado de la IMO 2020, celebrada en San Petersburgo, Rusia. El enunciado dice así:
Hay 4n piedritas de pesos 1, 2, 3, … 4n. Cada piedrita se colorea de uno de n colores de manera que hay cuatro piedritas de cada color. Demuestre que podemos colocar las piedritas en dos montones de tal forma que las siguientes dos condiciones se satisfacen:
- Cada montón contiene dos piedritas de cada color.
• Los pesos totales de ambos montones son iguales.
Ahora que escribo, viene a mi mente que, en aquella oportunidad, en la que se solicitaba ayuda financiera para costear el viaje de las jóvenes chapinas, alguien me indicaba sobre el porqué debía procederse a tal ayuda. Es decir, alguien se podría preguntar por las razones o motivos para tales apoyos. En este sentido, recién hemos hablado sobre la juventud y sus anhelos, que son nuestra luz y nuestra esperanza, para tantas cosas por mejorar en nuestro país. De hecho, la juventud ha dado muestras de un despertar ciudadano, que posee una consciencia propia, que no se deja alienar tan fácilmente.
En este sentido, conviene citar un par de pensamientos sobre el talento, y de cómo el mismo necesita de un terreno fértil para prosperar. El magnate estadounidense del acero, Charles Michael Schwab solía decir: «El talento es un recurso finito, mientras que la motivación es ilimitada». Algunos y algunas cuestionan el talento, calificándolo de un mito. No obstante, lo cierto es que el talento sí existe, pero no crecerá ni se sostendrá si no es conducido adecuada y pertinentemente. He ahí el sentido del apoyo y el acompañamiento. Como dice Galileo Galilei en nuestro epígrafe, no podemos enseñar, pero si podemos ayudar a que el talento florezca, a que se descubra por sí mismo.
El reconocido cineasta Steven Allan Spielberg, director y productor, considerado uno de los pioneros de la era del «nuevo Hollywood» escribe: «El talento sin oportunidades es como un árbol sin sol, no puede crecer ni prosperar». De manera similar, pero milenios antes, el célebre pensador de Atenas, Platón, decía: «El talento es como un árbol, el éxito es como su fruto; ambos dependen del cuidado que reciban». Este cuidado, el sol, la tierra y todos los elementos requeridos para el buen fruto, representan las ayudas que podemos brindar, en aquella ocasión financiera, en otro momento, posiblemente, de otro tipo.
Por otro lado, también es fundamental comprender que, al ayudar a la juventud, se otorga un apoyo que trasciende a las personas, pues se está, realmente, brindando apoyo al desarrollo, científico en este caso, de toda Guatemala. Aunque es lamentable que no existan fondos del Estado destinados a apoyar la ciencia y a la juventud que se encuentra interesada en su desarrollo, es importante fomentar la consciencia en torno de estos asuntos, invirtiendo el tiempo, recursos y energía en los y las jóvenes que se inclinan por el estudio de las ciencias, más aún en el caso de disciplinas tan poco comprendidas como sucede con la Matemática.
Deseo compartir que a Aby y Ana Julia las conocí en un evento webinario, de los que organizábamos para la secuencia Conversaciones en gAZeta, específicamente en el evento número 57, que llevó por título «Olimpíadas matemáticas: en qué consisten y qué nos muestran». De esto hace ya dos años. Empero, te invitamos a que veas el vídeo del programa, para agregar algunos elementos a los que ahora estamos compartiendo en el presente artículo. Para ello, pincha aquí. Los programas compartidos, aunque no interactivos, permitían recibir comentarios por parte de la teleaudiencia. En ellos, por ejemplo, se lee a Claudia Lara Galo, destacada educadora y matemática, quien expresa, en varios momentos, aspectos como los siguientes:
¡Excelente! Debemos dejar de enseñar a usar fórmulas para enseñar matemática […] De verdad muchas felicitaciones a las y los participantes […] Hay problema en la formación de maestros, desde la primaria. Debemos atender a eso y, definitivamente, desarrollar a todo nivel el pensamiento crítico.

Cuando Claudia expresa la importancia de «enseñar matemática», se refiere a la relevancia que tiene el quehacer matemático, como un proceso constructivo en sí mismo, no repetitivo, yendo mucho más allá de la aplicación algorítmica de fórmulas o procedimientos preestablecidos. Se trata del desarrollo de la creatividad, mediante una actitud lúdica y fundamentada en la curiosidad y la búsqueda del orden y la estructura que hay en todas las cosas, tanto sensibles como ideales.
También resulta oportuno comentar que, para que los y las jóvenes puedan representar a un determinado país en competencias de nivel internacional, es necesario que, previamente, se realicen competencias nacionales en las que resulten ganadores, con reglas similares a las utilizadas en las olimpíadas correspondientes. Como explicamos en lo previo, se trata del planteamiento de unos problemas matemáticos que se espera sean resueltos, con elegancia, creatividad e ingenio. Se trata, por lo general, de demostrar hechos que se presentan ante ciertas condiciones. Como hemos mencionado en el artículo «Conjeturas y teoremas», el meollo del trabajo matemático se basa en la demostración.
Regresando a las distintas olimpiadas, como hemos dicho, existen varios niveles de competición internacional, al igual de como sucede con los deportes físicos, mucho mejor conocidos. Específicamente están las siguientes, en orden creciente de cobertura, y, por lo mismo, de dificultad: a) Olimpiada Matemática de Centroamérica y El Caribe, –OMCC–; b) Olimpiada Iberoamericana de Matemática –OIM–; c) Olimpiada Panamericana Femenil de Matemáticas –PAGMO–; y, finalmente, d) la Olimpiada Internacional de Matemática –IMO–. En este sentido, Aby y Ana han participado en varias de estas competiciones.
Sobre nuestras representantes, Abigail Enríquez tiene 17 años cumplidos y estudia el V Bachillerato en el Colegio Monte María. Ella ha participado en la OMCC, obteniendo una mención de honor en 2021, siendo líder de la delegación 2022. También ha participado en la OIM, obteniendo una mención de honor, y en la PAGMO, con medalla de plata 2021 y medalla de bronce 2022. Por otro lado, Ana Julia Rojas, de 16 años, cursa el IV bachillerato en el Colegio Capoulliez. Ana Julia ha participado en la OMCC los dos años anteriores, habiendo sido acreedora a una mención de honor el 2022. También ha asistido exitosamente en la PAGMO del año pasado.
Con relación al tipo de problemas, deseo compartir una anécdota, que, además de alegórica, ilustra muy bien el desconocimiento que se tiene de esta hermosa ciencia, la Matemática, lo cual se agrava porque todos y todas, sin excepción alguna, hemos pasado por las aulas en cursos y en actividades educativas orientadas a aprender algo de esta disciplina, la cual, a la larga, termina siendo la gran incomprendida de todo el orbe. La anécdota remonta a más de 15 años atrás, cuando me desempeñaba en actividades varias en la coordinación académica y curricular en las aulas universitarias.
Resulta que, en cierta ocasión, le comenté al ingeniero que coordinaba el área de matemáticas al respecto del éxito que había tenido una estudiante en la recién pasada olimpíada: ella había ganado una mención honorífica. En aquellos entonces no sonaba mucho este tipo de eventos. El profesional, compañero de trabajo, expresó, despectivamente: «¡Qué gacho! … solo una mención honorífica». Además, me preguntó sobre qué tipo de asuntos se preguntaban en tales competencias. Yo le comenté que se planteaban problemas únicamente en las áreas de la geometría, aritmética, álgebra y combinatoria. Él contestó: «Pero, entonces, son cosas elementales, no le veo ninguna dificultad».
Aun comprendiendo yo que mi interlocutor no estaba del todo claro de qué se trataba, agregué que los problemas que se proponían eran inéditos, los cuales distintos matemáticos alrededor del mundo enviaban como propuestas a las directivas organizadoras de los eventos. «¿Pero no preguntan de Cálculo o Geometría Analítica?», inquirió. De mi parte seguía estando claro al respecto del desconocimiento de mi interlocutor, sobre lo que en Matemática elemental se puede incluir. Yo estaba seguro que mi colega nunca se había topado con un problema de la geometría plana elemental, de la geometría euclídea, o algo de aritmética, también llamada teoría de números.
En el intercambio, mi compañero me explicaba, muy orgulloso de sí mismo, que él había resuelto todos los problemas de esas áreas, que él, más que conocer, dominaba a la perfección. El tiro está en que, viendo que con palabras su horizonte de comprensión no cambiaría, y yo, un poco molesto, por la evidente prepotencia que manifestaba en sus comentarios, autoproclamándose en niveles de competencia difíciles de aceptar, decidí lanzarle una apuesta, a las que este colega era bastante aficionado. Le dije:
Mira, después de efectuadas las olimpiadas, siempre se publican los problemas de competencia. De hecho, se publican para que las chicas y los chicos que deseen participar tengan una referencia, una idea clara de hacia dónde van, en la búsqueda de las preseas o de algún reconocimiento. Si gustas, te traigo mañana los últimos tres años y si me resuelves uno de los problemas planteados, te habrás ganado Q 100.
Debo reconocer que me porté un tanto malvado (y con seguridad altanero también), pero al momento de mi reto estaba seguro de que, aunque mi colega coordinaba el área y manejaba muy bien la docena de cursos matemáticos que en la universidad se ofrecían, no poseía la más mínima idea del reto a vencer, y que su experiencia en demostraciones matemáticas era virtualmente nula. Lo que sucede es que, como hemos entrelineado arriba, el verdadero quehacer matemático es el de demostrar, no el de calcular o aplicar un algoritmo que te han presentado, y el cual puedes repetir, así como una máquina lo aplica, de manera mecánica y algorítmica.
El escritor y médico británico de ascendencia irlandesa, Arthur Ignatius Conan Doyle, escribió, en una de sus obras, sobre el célebre y talentoso detective de ficción Sherlock Holmes, lo siguiente: «La mediocridad no conoce nada superior a sí mismo, pero el talento reconoce inmediatamente el genio». Y esto viene a que se necesita escapar de la mediocridad circundante para reconocer y apreciar el valor que tiene el apoyo al talento, como sugiere el epígrafe, en la relevante actitud en pro de este requerido apoyo a nuestros congéneres que tienen la chispa fresca, en decidido favor de la edificación de una mejor humanidad.
Ni se diga lo que sucedió con el colega que he citado. Se esfumó, y al cabo de varias semanas, yo, un tanto en broma, un tanto inquisidor, le pregunté, «¿Cómo te fue?». «¿Con qué?», me contestó. Al recordarle del reto en torno de los problemas de la IMO, me expresó, así como un tanto indiferente, que no había tenido tiempo para eso, que estaba en «cosas más importantes». Estaba claro, a todas luces, lo que realmente había pasado. De suerte que no aposté en doble vía, porque tampoco quería herir al compañero, es decir, si el perdía la apuesta, si no podía con alguno de los 18 problemas que le copié, él no me pagaría nada.
Recuérdese que las competencias consisten en dos días consecutivos en los que se plantean tres problemas, dando 4.5 horas para su posible resolución. Por la inquietud que posiblemente se ha incrustado en la mente de quien nos lee, deseo compartir que la página de la IMO tiene a disposición de todo el público los problemas de las olimpiadas realizadas. Basta ir y pinchar en el siguiente enlace: Problemas IMO. Empero, en la imagen siguiente hemos hecho el esfuerzo de conservar la resolución visual, para que, con un acercamiento, puedas leer algunos de los problemas de los tres años previos. A continuación, copiamos dos de los problemas planteados.

- Hallar todas las ternas (a, b, p) de números enteros positivos con p primo que satisfacen: ap= b! + p
- Sea n > 100 un entero. Iván escribe cada uno de los números n, n + 1, … 2n en un naipe diferente. Después de barajar estos n + 1 naipes, los divide en dos pilas distintas. Probar que al menos una de esas pilas contiene dos naipes tales que la suma de sus números es un cuadrado perfecto.
Alguno, alguna, pensará: «¡qué sufrimiento!». Esto me recuerda a Confucio, que decía: «Elige un trabajo que te guste y no tendrás que trabajar ni un solo día de tu vida». El gusto y atractivo por la Matemática es algo que viene con la vida misma, algo que no se puede evitar. Pasamos ahora a nuestro problema de ilustración. Aunque hemos conversado sobre el fallido sistema educativo formal, viene al caso comentar que han venido apareciendo magníficos apoyos audiovisuales, vídeos, dedicados a compartir la resolución de problemas matemáticos simples, pero que requieren de gran ingenio y mucha creatividad. De uno de estos nuevos canales estamos tomando lo que sigue, a manera de ilustración.
Estos apoyos audiovisuales de la multimedia son verdaderas joyas, que hace apenas una o dos décadas atrás no era imaginable poseer, como expreso, al alcance de la mano. Ciertamente, en el muy conocido YouTube, existen canales de difusión matemática y científica que son altamente recomendados. Claro, y esto es relevante, no todo lo que circula en las redes representa un aporte valioso, pues hay quienes, tratando de transmitir una aparente labor formativa en sus canales personales, son en definitiva un desastre educativo y todo lo contrario de lo que estoy elogiando.
Al margen de estos malos difusores, deseo compartir con el lector y lectora un par de magníficos canales de difusión. Uno ya lo he mencionado anteriormente, cuando tratamos el tema de los modelos matemáticos para la analítica epidemiológica: el canal titulado 3Blue1Brown. Otro, que ahora traigo a colación, es el canal MindYourDecisions de Presh Talwalkar. Presh aborda ciertos problemas, que magistralmente procede a resolver con la técnica del vídeo animado. Los problemas provienen, a su vez, de las propuestas que terceros le envían, desde distintas partes del mundo, y que destacan de manera particular por su sencillez y el ingenio con el que se resuelven, siendo algunos tomados de las competencias olímpicas en donde se han planteado.
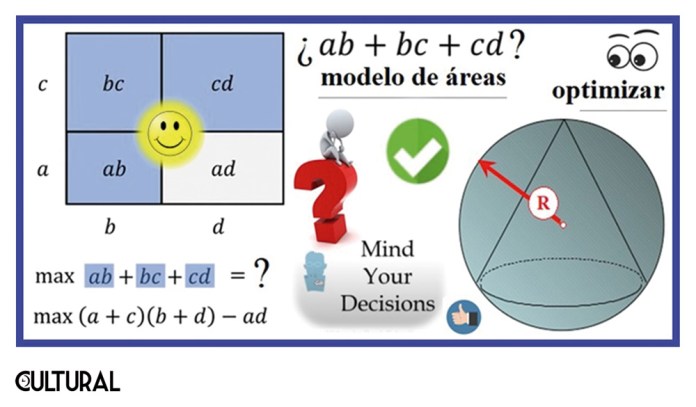
En general, los problemas propuestos en las olimpiadas se escogen, grosso modo, entre varias áreas de la matemática de la escuela elemental, sin superar lo incluido en la educación secundaria. No se requieren conocimientos de matemáticas superiores, y se espera que las soluciones sean cortas y elegantes. Sin embargo, encontrarlas requiere de un ingenio excepcional y del talento matemático genuino que las competencias persiguen evaluar. Aunque los ejemplos incluidos en la imagen precedente se refieren a números, en su mayoría, los hemos colocado así por la naturaleza del problema que desarrollaremos en este artículo, que es sobre una optimización en números enteros.
También es relevante comentar que lo relacionado con geometría y lógica es, en efecto, medular, como en algunos problemas de teoría de juegos, combinatoria u otros, para nada cuantitativos. Estoy seguro de que el lector se encuentra menos familiarizado con el trazo y el razonamiento geométrico, además, que la redacción se vuelve más intricada y extensa en el caso de los juegos. En esta línea de ideas, para ilustrar que «lo matemático» no tiene por qué referirse a cosas de números, copio otro problema olímpico:
Un arreglo regular de focos de 5 × 5 está defectuoso, ya que al apagar o encender el apagador de uno de los focos provoca que cada foco adyacente en la misma columna o en la misma fila, además del foco mismo, cambie de estar encendido a apagado o de apagado a encendido. Inicialmente todos los focos están apagados. Después de apagar o encender los apagadores varias veces, solo un foco permanece encendido. Encuentre todas las posibles posiciones de este foco.

Pasando al problema que Presh Talwalkar resuelve, en este vídeo del canal MindYourDecisions, copio el enunciado:
Se sabe que cuatro enteros positivos, denotados por a, b , c y d, suman 63 (esto es: a + b + c + d = 63). Con esta condición, se pide encontrar el valor máximo de la expresión ab + bc + cd, y para qué valores se obtiene este valor óptimo.
Lo primero es comprender el problema, como bien explicó el matemático húngaro George Pólya, en su libro How to solve it (1945, el original en inglés), Cómo plantear y resolver problemas, en el cual describe su método, o heurística, de cuatro pasos. También conviene simplificar el planteamiento, para entender la pregunta. Para ello, suponga el lector que tenemos únicamente dos números, a y b, y que se cumple que suman 20. Se pide entonces determinar cuál es el máximo del producto de ellos. Esto, en símbolos de letras, se escribiría así: sabiendo que a + b = 20, se pide averiguar el máximo valor del producto ab.
Entonces, para explorar la situación, procedemos a inventamos una respuesta, para ver si tiene sentido la pregunta que nos hacen. Por ejemplo, se puede tomar como solución, inventada, la siguiente: a = 5 y b = 15. Así, podemos verificar que se cumple que a + b = 5 + 15 = 20 y se tiene que ab = (5)(15) = 75. Por otro lado, si tomamos a = 7 y b = 13, entonces, además de que la condición se cumple (a + b = 7 + 13 = 20), se tendrá que ab = (7)(13) = 91.
Entonces comprendemos que la pregunta tiene sentido, pues si sabemos que la suma de dos números enteros positivos es conocida, en este ejemplo 20, el producto no está para nada determinado, es decir, es variable. De esta forma tiene sentido preguntar cuándo este valor del producto de los dos números seleccionados es máximo. Como se pide que los números sean enteros positivos, sabemos que existe un número finito de casos a considerar, que corresponden exactamente todas las opciones desde a = 1 hasta a = 20.
El lector puede probar, mentalmente o con auxilio de un calculador, todos los casos posibles y encontrar que el máximo producto para ab es 100, que se obtiene cabalmente en a = 10 y b = 10. En cualquier otro caso, el producto será inferior a 100, como trata de ilustrarse en la imagen que sigue.
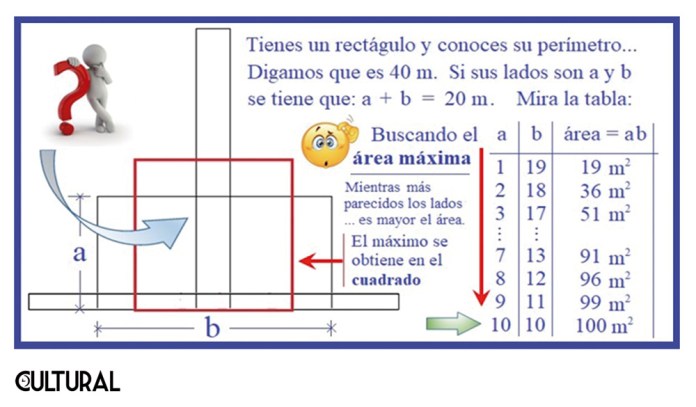
En el problema anterior, el de encontrar el máximo producto de dos números enteros, conocida la suma, no solo se puede repetir con otros parámetros (en este caso el valor de la suma), sino que no es difícil que un joven o un niño se percate de las relaciones subyacentes en tal situación. En el caso más frecuente, muy posiblemente un joven en secundaria se entere, justamente, cuando le piden resolver aquellos casos de factorización de trinomios cuadráticos asociados al problema. En estos casos se pide encontrar dos números tales que, sumados den un cierto valor, pero que multiplicados den otro. Por ejemplo, en la expresión x2 – 8x + 12, se quiere dos números que multiplicados den 12, pero que sumados den 8. La respuesta, de 2 y 6, permitirá escribir que x2 – 8x + 12 = ( x – 6 ) ( x – 2 ), lo que a su vez indica que las raíces, o ceros, del polinomio cuadrático son justamente 2 y 6.
En el ejemplo anterior, la respuesta numérica en sí no es lo importante (y en esto falla la educación estándar, según hemos comentado), sino las observaciones matemáticas que del problema podemos realizar. Nótese, por ejemplo, que: al considerar todas las posibilidades de los enteros que multiplicados den 12, se cae en la cuenta de que la suma es mínima cuando los dos números propuestos son lo más parecidos posibles, en este caso 3 y 4, que suman 7. En forma alterna, la suma es máxima cuando los dos números son lo más distante posibles, lo más distintos entre sí, que serían 1 y 12, que suman 13. Otra observación relevante es que la anterior aseveración adquiere una modalidad dual, que es: dada la suma, el producto será máximo cuando los dos números son lo más parecido posibles (que es la dual de la precedente: dado el producto, la suma será mínima cuando los dos números son los más parecidos posibles).
En la imagen previa se ilustra geométricamente el hecho, pues si se conserva el perímetro de un rectángulo (esto es, la suma de sus lados), el área será máxima cuando los lados sean lo más parecido posibles. En nuestros ejemplos numéricos, si la suma es 20 (perímetro 40), el máximo producto (área) se obtiene con los lados 10 y 10, correspondiente a un cuadrado, de forma similar a si la suma fuera 8, en cuyo caso el máximo producto será obtenido con los lados iguales, de 4 y 4.
Este fenómeno de que los óptimos reflejan cierta simetría es frecuente, y un joven con talento matemático lo observará con facilidad, digamos de manera intuitiva, aunque no cuente con el rigor del lenguaje matemático. Por ello se dice que hacer matemáticas se reduce al aprendizaje de cómo escribir en el lenguaje matemático, sobre cómo aprender a escribir algo que se comprende, que se «entre lee» en lo que se observa, que se es capaz de inteligir en las relaciones que se descubren en las cosas. Así, el quehacer matemático no es más que un juego mental de relaciones abstractas que se dan en algunos fenómenos, y que pueden ser aplicadas en otros. En la tercera y última entrega, cerraremos el problema que nos ha motivado, reforzando esta curiosidad de la dualidad en los procesos de optimización, y traeremos a la mesa otra peculiaridad del pensamiento matemático: el isomorfismo.
Recapitulando, al inicio hemos incluido una breve descripción de las competencias olímpicas en Matemática, cuya primera modalidad, la IMO, lleva ya 62 años celebrándose. Lo hicimos como preámbulo de la presentación del problema que hemos planteado, tomado de las olimpíadas intermedias de Australia, del año 2013, para estudiantes talentosos en las edades de 7 a 10 años, quienes disponen de un tiempo medio de veinte minutos para su resolución. Siguiendo las recomendaciones del matemático G. Polya, procedimos a una simplificación.
Dados dos números a y b, y conociendo su suma, se pide determinar cuándo se obtiene el máximo producto. La exploración del sentido del problema se realizó con números más simples aún, puesto que se asumió que la suma de estos dos números a y b era 20, es decir, se asume que a + b = 20 y se pide encontrar el máximo del producto ab. En lo previo se verificó que esta simplificación del problema tiene total sentido, pues, aunque sepamos que dos números suman 20, el producto entre ellos no está determinado. Por ejemplo, 2 y 18 suman 20, y su producto es 36, mientras que 5 y 15 suman 20, pero su producto es 75.
También se incluyó una imagen que ilustra que el máximo producto se dará cuando ambos números sean los más cercanos posibles, y como en este caso son 10 y 10, que suman 20, el máximo producto será 100. Invitamos a repetir con otro valor de suma y se observa el mismo fenómeno. En aquel momento comentamos un principio de dualidad de los problemas de optimización. Si se conoce la suma, el máximo producto se obtiene con los números más cercanos entre sí, cuya formulación dual es: si se conoce el producto, la mínima suma se obtiene en la misma condición, que los números sean lo más cercanos entre sí.
La dualidad se refiere al cambio de máximo a mínimo y viceversa. Este es un auténtico hecho matemático, y como el lector podrá apreciar, se trata de enunciados con palabras y con conceptos de naturaleza formal, como lo es la noción de óptimo.
Por otro lado, es el momento de regresar a la imagen última, en la cual se colocaron algunos ejemplos de otros problemas de optimización, para hacer la siguiente observación de los mismos. Resulta que si se pregunta cuál es el máximo producto de dos números enteros, a y b, pues no existe problemática alguna, porque el producto ab no está acotado y podría crecer sin límite, haciendo cabalmente los dos factores a y b inmensamente grandes.
Sin embargo, cuando se dice que ambos números son positivos y suman una cantidad S, entonces la cuestión cambia. Vemos que el valor del factor a tiene un valor mínimo, que es 1, y un valor máximo, pues no puede ser ni igual, ni mayor que S, siendo este valor máximo S – 1. En el caso en que S = 20, sabemos que cada uno de los números intervinientes varían desde 1 hasta 19. Hay un problema de optimización porque hay una condición que limita las cantidades que intervienen en la pregunta.

Esto es general y es lo que se ilustró en la imagen que hemos copiado nuevamente. En la esquina superior izquierda se muestra una esfera. Si se pide el cono óptimo bajo estas circunstancias, se puede intuir que la pregunta interesante refiere al cono máximo, porque se visualiza que los conos mínimos serían aquellos de volumen cero. Nuevamente, para que la pregunta haga sentido, será necesario fijar el tamaño de la esfera, indicando que el radio de la esfera no es variable. Claro, en este caso puede sobreentenderse y únicamente preguntar: ¿cuál es el cono más grande que puede meterse adentro de una esfera? O de forma más precisa, podría especificarse: encuentre las dimensiones del cono circular recto que puede ser inscrito en una esfera de diámetro 20 cm.
En la esquina superior derecha de la imagen previa, se muestra algo relacionado con la fórmula de Brahmagupta y con los cuadriláteros en general. Resulta que, si se conocen los valores de los cuatro lados de un cuadrilátero, el mismo no queda determinado, pero sí lo estará el área máxima que se puede obtener con esos lados. El óptimo viene dado por el cuadrilátero cíclico, esto es, el obtenido al inscribir el cuadrilátero en una circunferencia, que puede interpretarse como el cuadrilátero «más redondo» que sea posible construir. En el centro de la imagen, el problema actual, relacionado con el problema isoperimétrico.
Recalcamos la simetría en los casos mostrados. Identificamos un máximo porque, partiendo desde un caso nulo, llegamos, de manera continua, a otro que vuelve a anularse. La variable que se desea optimizar empieza creciendo, para después terminar en descenso. La intuición dice que habrá un valor en el que deja de crecer y empieza a bajar, y en ese justo punto se tendrá un valor máximo. En el caso del cono, partimos de un cono aguja, super delgadísimo, y lo vamos abriendo, y abriendo, hasta llegar a otro tan abierto, que vuelve a tener volumen cero. Este hecho matemático se conoce actualmente como el teorema de Rolle, y fue establecido en 1691 por el matemático francés Michel Rolle.
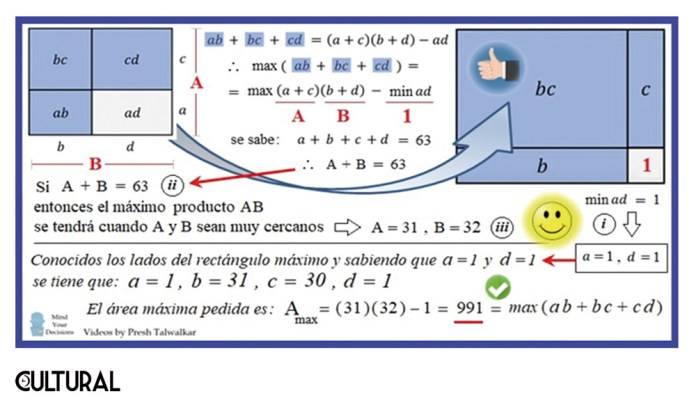
Después de estas observaciones, la resolución de nuestro problema no resultará ya tan lejano. La síntesis en la imagen precedente. El paso genial se da con la observancia de que la expresión objetivo (ab + bc + cd) corresponde isomórficamente a un modelo de áreas, partiendo de un rectángulo de lados (a + c) y (b + d). Se persigue maximizar el rectángulo, pero excluyendo el término ad. En la imagen previa se aprecia el modelo, en el cual el niño observa que se pide maximizar el área sombreada, bajo la condición de que los dos lados (A y B) sumen 63.
El siguiente punto será notar que, para maximizar el área sombreada, el término faltante, que es ad, debe minimizarse, lo que se logra con a = 1 y d = 1, obtenidos de ad = 1. Por lo explicado, si sabemos que la suma de los lados es 63, ya hemos apuntado que el producto máximo se obtendrá con los lados 31 y 32, que son los números más parecidos posibles que suman 63. De todo ello, el resultado buscado será (32)(31) – 1 = 991.
El lector puede estudiar la imagen previa y ver detenidamente los pasos a seguir: i) dibujar la cuadrícula; ii) minimizar ad, que implica: a = d = 1; iii) un rectángulo con suma de lados 63, tiene su área máxima con lados 31 y 32; iv) concluir que el área máxima es todo el rectángulo menos ad.
Al medio de nuestros comentarios, escribíamos que el gusto y atractivo por la Matemática es algo que viene con la vida misma, algo que no se puede evitar. Realmente, se trata de un placer innato que alimenta, aun cuando no se sea tan talentoso, o exitoso, en lo que se emprende. Se trata de una profunda satisfacción que se desarrolla con la aventura racional y que se acrecienta con los laberintos en los que, inevitablemente, se debe penetrar, buscando una ansiada comprensión de aquello que tanto atrae, quizá por lo imposible, quizá por lo posible, a la manera de un amor muy personal, íntimo e inexorable. Así que, cerramos con nuestros mejores deseos para Aby y Ana Julia en su experiencia IMO, allá en Chiba, Japón.