El 2024 y la diferencia de cuadrados
Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
El matemático puro como el músico, es un creador libre de un mundo de belleza ordenada.
Bertrand Russell
En los últimos años, se ha venido convirtiendo en tradición escribir alguna curiosidad o notable propiedad sobre el número correspondiente al año que inicia, a manera de diversión y con el ánimo de aprender algunos conceptos matemáticos interesantes. También resultan curiosas las ideas que se tienen en torno de los números. Hemos insistido, en distintas oportunidades, que la Matemática no trata sobre números exclusivamente, pero he observado que, de los sistemas matemáticos, es muy frecuente que lo numéricos resulten muy atractivos a muchas personas. Quizá porque es lo que más hemos abordado en la escuela, aunque, a decir verdad, posiblemente nos estamos perdiendo de algunas cuestiones igualmente placenteras, por no haber tenido la oportunidad de apreciarlas en su justa dimensión.
En este sentido, en nuestro epígrafe, debido al filósofo, matemático, lógico y escritor británico, Bertrand Arthur William Russell, se habla de un mundo de belleza ordenada, lo que seguramente sorprenderá a quien nos lee. Hablar de belleza de algo que usualmente asociamos con tormentos y dificultades no pareciera ser un indicador de salud mental. Empero, el filósofo británico no se equivoca. En la misma línea, el connotado científico alemán, ciertamente más sonado en la voz popular, Albert Einstein, decía: «La matemática pura es, a su manera, la poesía de las ideas lógicas». Acá, se sobreentiende que con el término «poesía» nos estamos refiriendo a una manera hermosa de expresar las cosas. Nuevamente, la belleza es el concepto central.
No obstante, al margen de un posible desconocimiento de ese mundo al que grandes personalidades se han referido como algo hermoso, podemos jugar con alguna aproximación que nos permita acercarnos un poco más a este orden poético que tantas frases inspiradoras ha motivado. En esta ocasión, presentaremos una curiosidad del número del año que estamos iniciando: 2024. Tuve la oportunidad de escuchar de varias personas conocidas que «este era un número bonito». Me ha hecho reflexionar sobre el porqué a muchas y muchos agrada, al menos más que el 2023, que recién ha terminado. Advierto, no hablamos de los acontecimientos o nuestras expectativas, sino del número en sí.

Imagen N° 1
Respecto a los propósitos de inicio de año, comparto que estamos en la intención de facilitar, quizá de manera más enfática y apropiada, algunos de los conceptos matemáticos que hemos venido abordando. Por ello pensé en conversar sobre alguna cuestión «no tan complicada» referida al número en cuestión. Entonces uno piensa, ¿qué de particular podría tener el número 2024? Primero, comprender que no hablamos del numeral, en sistema decimal en este caso.
Recordar que el numeral es la secuencia de un signo 2, seguido de un 0, un 2 y un 4. Lo primero que generalmente se dice, es que estos dígitos son pares. Al hacer una encuesta libre, sobre qué número es más agradable, entre el 2023 y el 2024, es casi seguro que las opiniones se inclinarán por el 2024, porque es par y tiene números pares. Sin embargo, deseo comentar que los matemáticos puros han demostrado, a lo largo de la historia, una propensión diferente.
De hecho, los antiguos pitagóricos gustaban de los impares. Por otro lado, por la misma definición de lo que es un número par, esto es, divisible por dos, un número par nunca será un número primo, con la única excepción del mismo 2. Cuando hablamos de números, es importante recordar que nos sirven para contar y para medir, lo que nos presenta una diferencia importante en el tipo de números. Véase la siguiente imagen, en la que aparece el tipo de variables que solemos utilizar. Distinguimos entre las cantidades discretas, que utilizan números enteros positivos (naturales, como se les llama en Matemática, los que incluyen el cero), y las cantidades continuas, que recurren a números que aceptan fraccionamiento o división.
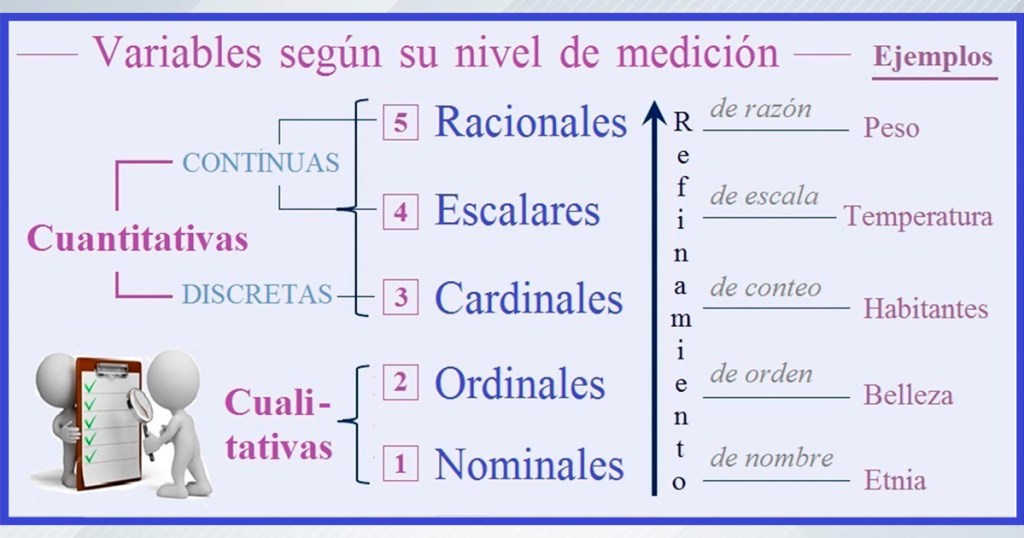
Imagen N° 2
En la imagen que sigue se colocan los conjuntos numéricos más conocidos, entendiendo que al descender vamos ampliando el concepto de número. Los números primeros o más básicos son los naturales: ℕ = {0, 1, 2, 3…} Ya sabemos que los puntos suspensivos indican que la secuencia continua sin finalizar, que el conjunto es infinito. Estos números naturales son los que nos sirven para contar. En el caso del 2024, sabemos que implica una cuenta de años desde un momento inicial. Cada año que transcurre, el número irá incrementando en una unidad.
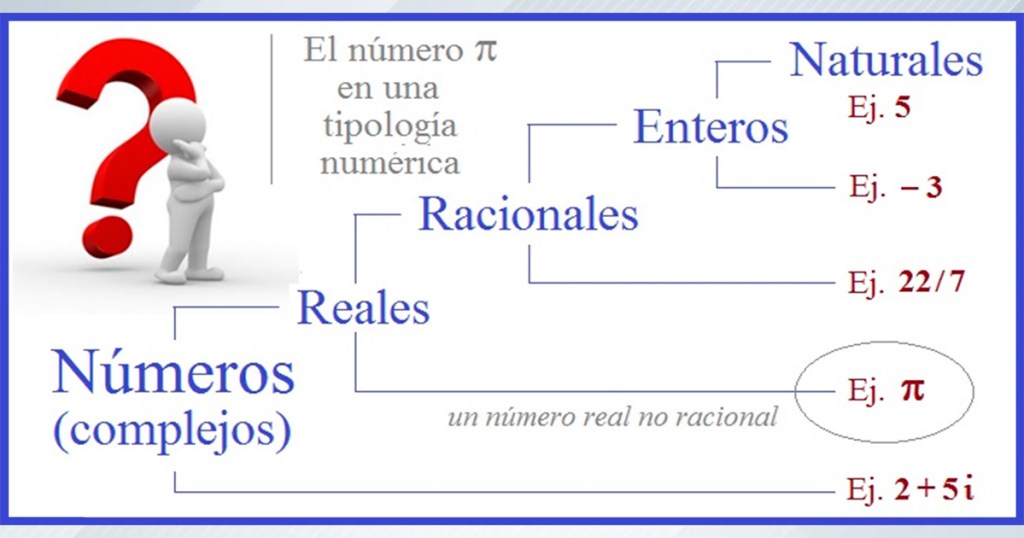
Imagen N° 3
Esta predilección popular por los números pares la comentamos en el artículo «El reloj y la aritmética modular». Los números pares constituyen un subconjunto de los números naturales que es cerrado, tanto en la suma, como con el producto, lo que significa que al sumar o multiplicar pares, seguirás obteniendo pares. Se habla de cerradura porque no puedes salir. Imagínate en un mundo en donde todos los habitantes son pares… nunca podrías salir de ese mundo, porque nunca podría aparecer alguien que no es par, precisamente por lo anterior. Observa la tabla de las operaciones de la aritmética de módulo dos, es decir, de los pares y los nones. El 0 representa los pares y el 1 los impares.
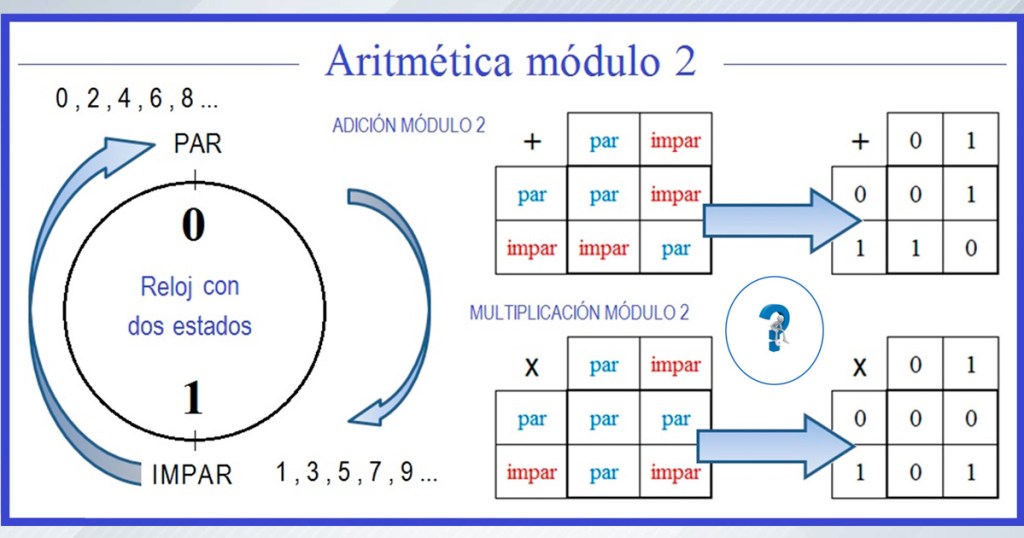
Imagen N° 4
Claro, existen más tipos de números, además de los pares y los impares. Esta característica no reviste mayor interés, porque sabemos que a un año impar sigue un par y viceversa. Decir que 2024 es par es correcto, pero no podríamos decir que esa es una propiedad interesante. Además de las aritméticas módulo k, o de los múltiplos de un cierto número natural, existen otras formas de clasificar los números u otros tipos de números especiales. De hecho, se pueden inventar ese tipo de categorías o de formas de clasificación.
Por ejemplo, podemos hablar de números triangulares o de números cuadrados. Observa la siguiente imagen. Ves allí que el 10 es triangular, porque puedes hacer un triángulo con 10 fichas, y que el 16 es cuadrado, porque puedes hacer una cuadrado con 16 fichas. Con relación a esto, el año que viene, 2025, será cuadrado, dado que 2025 = 45 x 45 = 452. Esto lo menciono porque tiene que ver con lo que pasaremos a ver. De hecho, cuando pensé en el 2024, lo relacioné con el 2025.
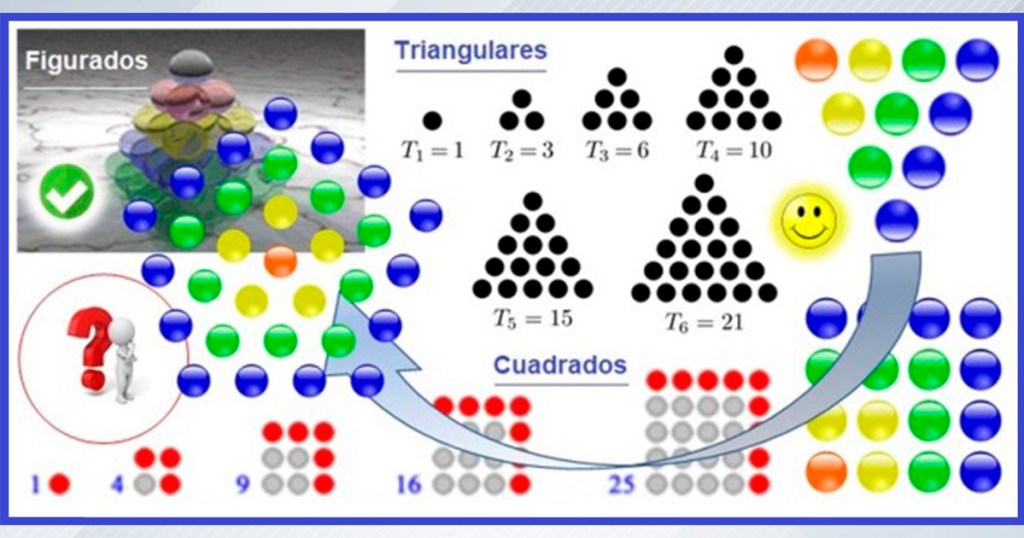
Imagen N° 5
De manera indirecta estamos manejando ya un concepto crucial, que es el de divisibilidad, o de divisores. Decimos y sabemos que 2024 es par, porque es divisible por 2, o sea que 2 es un factor de 2024. Lo demostramos al escribir: 2024 = 2 x 1012. Lo importante es que 2024 es de la forma 2n, donde n es un número natural. Por otro lado, 2025 = 45 x 45, lo que significa que es múltiplo de 45, que es lo mismo que decir que tiene la forma 45n, donde, nuevamente, n es algún número natural. Entonces, para todo número natural podremos formar una determinada colección con todos los divisores, o factores, del mismo.
Sobre este punto, podemos mencionar a un filósofo y matemático neopitagórico, llamado Nicómaco de Gerasa, que vivió, cerca del año 100 d. C., en lo que actualmente es Jordania. Nicómaco escribió Arithmetike eisagoge (Introducción a la aritmética), un tratado de gran influencia posterior, en la que clasificó a los números naturales en tres tipos. Véase la imagen siguiente. El número 6 es perfecto, sin defecto y sin exceso. La mayoría de números son defectuosos, porque sus divisores propios suman menos que ellos mismos. Empero, 2024 es excesivo, pues sus divisores propios suman 2296. Puedes consultar esto en este enlace.

Imagen N° 6
En fin, que existen muchas formas de jugar con los números, de donde surgen distintas formas de clasificarlos. Por ejemplo, en el artículo «La cortesía de un número» tratamos justamente ese concepto, mostrando un método mediante el cual podemos asignar a cada número natural una determinada magnitud de la cortesía que tiene. Este tipo de asuntos no son estrictamente importantes para el edificio formal de la Matemática, sino, más bien, vienen a constituirse como parte de un área denominada matemática recreativa. En contraposición, un punto que sí reviste gran importancia es este asunto de la factorización.
Resulta que, en el caso de los números naturales, cuando los expresas como un producto, es decir, cuando los descompones en dos factores, puedes continuar el proceso, descomponiendo estos primeros factores hasta que ya no se pueda seguir descomponiendo la expresión. Es así como llegas a una representación factorial en números primos, que significa que has colocado el número como un producto exclusivo de números primos, los que ya no pueden ser descompuestos, porque no tienen divisores, aparte de la unidad. En el caso de nuestro número 2024, en el enlace previo se indica que 2024 = 2 x 2 x 2 x 11 x 23 = 23 x 11 x 23, como se muestra en nuestra primera imagen.
Este proceso de factorización en primos siempre es posible, obteniendo como resultado una representación única de cada número natural. Esto es lo que asegura el denominado teorema fundamental de la aritmética. En la imagen siguiente se muestran los casos de los números 5, 6 y 1200. No importa cuál sea el número natural que escojas, siempre este número tendrá una cantidad finita de números primos y estos quedan totalmente determinados por el número en cuestión. Por ello se habla de una factorización única. Los factores determinan el número y el número determina sus factores. En algún momento uno podría pensar que esto tiene que ser así, que es un resultado obvio.

Imagen N° 7
Sin embargo, el quehacer matemático consiste en indagar si aceptando algunos supuestos primarios, llamados axiomas, es necesario que se sucedan algunas cosas, las cuales posiblemente se visualizan como esperadas o naturales. El camino hacia el desarrollo matemático actual ha tenido momentos de especial lucidez, en donde se descubren sistemas matemáticos que prueban que existen excepciones a eso que posiblemente se está visualizando como lo naturalmente esperado. En este caso una pregunta girará en torno de lo que significa que un número sea «entero».
Aunque no es el objetivo, deseo mencionar un par de asuntos relacionados al tema de factorización. El matemático, astrónomo y físico alemán, Johann Carl Friedrich Gauss, extendió el concepto de número entero, proponiendo los que ahora se denominan enteros gaussianos. Entonces descubrió que en algunos sistemas se daba la factorización única, pero que en otros no sucedía así. Además, observó que el concepto de número primo no era universal, esto es, que un cierto número podía ser primo en un sistema, pero en otro no. En la imagen precedente se ilustran ambas situaciones.
Primero, se nota que el número 5 es primo en los naturales, es decir en el sistema ℤ[1], pero no lo es en el sistema ℤ[i], porque 5 es factorizable en dos enteros: 5 = (2 + i)(2 – i). También, lo que es más trascendente, es que, en un cierto sistema aritmético, podría darse que un mismo entero posea más de una factorización en números primos, como se muestra para el caso del entero 6, dado que hay dos factorizaciones en números primos, a saber: 6 = 2 x 3 = (1 + √5 i)(1 – √5 i). Esto último sucede en el sistema ℤ[√5 i].
En la siguiente imagen, abajo, en la derecha se muestra un diagrama con los tipos de sistemas a los que estanos haciendo referencia. Un DFU es un dominio de factorización única. Resulta que los números naturales (los enteros ℤ , realmente) cumplen con ser un DFU, pero hay otros sistemas enteros, dominios integrales, DI, que no son DFU. Todos estos conceptos y relaciones se estudian en la teoría de anillos, un hermoso e inquietante capítulo del algebra abstracta. Para el lego, la moraleja es que los matemáticos puros estudian las condiciones que deben darse para que ciertos resultados se cumplan, y que existen muchos sistemas además de los usuales que suelen presentarnos en los estudios de la escuela elemental
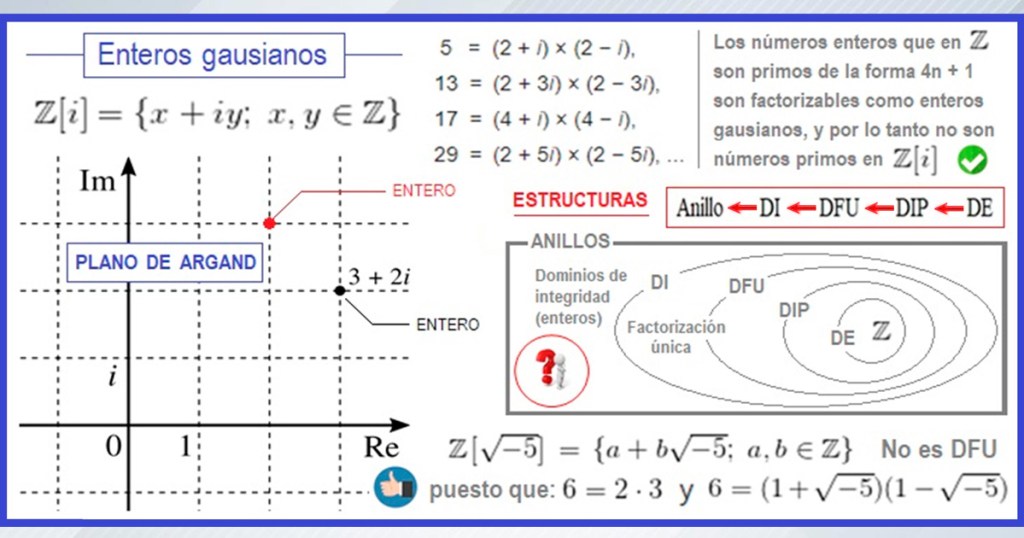
Imagen N° 8
Momento de entrar a lo que deseamos presentar para mostrar una propiedad que cumple el 2024, para luego evaluar qué tan singular o común es tal propiedad. En este sentido, ya hemos dicho que el 2024 es un número par, divisible por 2, pero también hemos aclarado que tal situación no es nada especial, porque muchos, de hecho «la mitad» de todos los números naturales, son pares. Pues bien, como he comentado más arriba, al pensar en el 2024, pensando un tanto en el año que pasó, como en el que viene, me percaté que el siguiente, 2025, es un cuadrado perfecto. Esto significa que 2024 = 2025 – 1 = 452 – 1.
Alguna persona me podría decir que 2024 = 2023 + 1, lo que realmente no aporta mayor información. Lo que sucede es que, la anterior expresión corresponde a una famosa forma algebraica, denominada «diferencia de cuadrados». Quizá alguien recuerde la expresión a2 – b2, y acierta en sus remembranzas. Resulta que tal binomio corresponde a uno de los llamados productos notables, específicamente, a una identidad que reza así: a2 – b2 = (a – b)(a + b). En este punto quizá regresar a un segmento de nuestro artículo, «Algunas demostraciones visuales», siempre acá en los Suplementos Culturales LaHora. Véase la siguiente imagen tomada de la citada publicación, en la cual se ilustra la identidad algebraica prescrita.
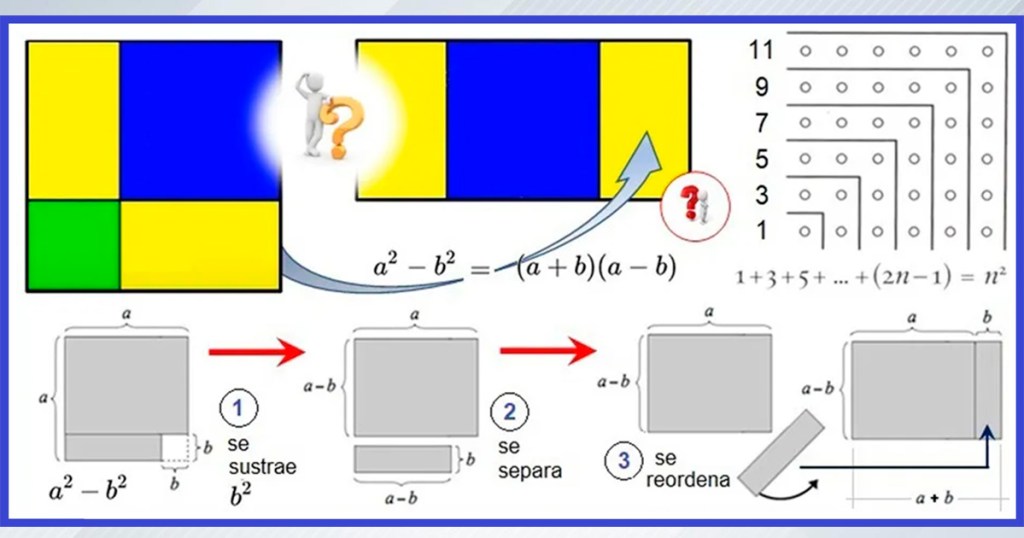
Imagen N° 9
En el caso que nos ocupa, al notar que 2024 es una diferencia de cuadrados, veremos que podemos proceder a expresarlo como un producto, puesto que eso es lo que dice la anterior identidad, que cuando una cantidad se puede colocar en la forma a2 – b2, también podrá ser escrita como su equivalente, (a – b)(a + b), dado que: a2 – b2 = (a – b)(a + b). De esta forma, tenemos que: 2024 = 2025 – 1 = 452 – 12 = (45 – 1)(45 + 1) = 44 x 46.
A su vez, se tiene que 44 = 4 x 11 = 2 x 2 x 11, y 46 = 2 x 23. Nótese que tanto 2, 11 y 23 son números primos, es decir, que ya no pueden descomponerse en factores más pequeños, de manera que la factorización en número primos de 2024 viene dada por: 2024 = 2 x 2 x 2 x 11 x 23 = 23 x 11 x 23. Obsérvese este procedimiento en la imagen siguiente.

Imagen N° 10
En conclusión, hemos llegado a la representación multiplicativa final de 2024, en donde aparecen los números primos 2, 11 y 23, únicamente. Como el 2 aparece tres veces, 2024 contiene cinco números primos en su factorización. Así, podríamos decir que 2024 ∊ P5, puesto que contiene cinco factores primos en su representación multiplicativa, que, como hemos mencionado, es única. La propiedad que le hemos traído a colación es que 2024 es una diferencia de cuadrados. Específicamente, 2024 = 452 – 12. La pregunta ahora es si esta característica, la de ser una diferencia de cuadrados, es una propiedad frecuente y bastante común, o se trata de una peculiaridad y una propiedad singular.
Para responder a ello, será conveniente regresar a la fórmula: a2 – b2 = (a – b)(a + b). La pregunta es si existen números naturales a y b que puedan cumplir que a – b es un factor, mientras el factor complementario es a + b. Dicho de otra forma, después de factorizar el número N que deseamos colocar como una diferencia de cuadrados, lo podremos expresar como N = pq, asumiendo que p < q. Entonces deberemos pensar que la expresión a – b será p mientras que a + b será q. ¿Cómo podríamos resolver este sistema de ecuaciones: p = a – b | q = a + b?
La solución viene dada por la semisuma y la semidiferencia. Veámoslo con un ejemplo. Supóngase que se sabe que la suma de dos números desconocidos es 20, mientras que su diferencia es 10. Lo que estamos afirmando es que el número mayor vendrá dado por la semisuma, ½ (20 + 10) = 15; mientras que el número menor vendrá dado por la semidiferencia: ½ (20 – 10) = 5. En efecto, la suma de 15 y 5 es 20, mientras que la diferencia entre 15 y 5 es 10. En la imagen que sigue se muestra el proceso para el caso de 1 x 9 y de 11 x 23.
El tiro, al final de este proceso, es que hemos encontrado los números cuya diferencia de cuadrados es los que se desea. Así, puede verificarse que: 1 x 9 = 9 = 52 – 42 y 11 x 23 = 253 = 172 – 62. El caso nuestro es 2024, que se factoriza como 44 x 46, de donde se obtiene una diferencia de cuadrados dada por 452 – 12. Al razonar la situación, dado un número cualquiera, o sea, dada una representación cualquiera de factores primos, siempre, se podrá encontrar una suma de cuadrados para el número, con una única excepción.
Partiendo de N = pq, la semisuma ½ (p + q), o la semidiferencia ½ (p – q), no serán enteros únicamente si p y q no coinciden en paridad, es decir, si uno es par y el otro es impar. Por ello, todos lo números naturales se pueden colocar como diferencia de cuadrados, a menos que sean de la forma «2 x impar», como es el caso de 30 = 2 x 15. Se haga lo que se haga, 30 nunca será la diferencia de cuadrados de dos números naturales. No obstante, el caso general, o más frecuente, no cae en esta situación.

Imagen N° 11
Por ello concluimos que la propiedad de expresar a 2024 como una diferencia de cuadrados no es, realmente, algo excepcional, sino todo lo contrario, muy frecuente y bastante fácil de encontrar. Esto contrasta con la propiedad que presentáramos para el 2022, en el artículo «Factores y factoriales para un nuevo año», en la que hicimos uso del factorial de un número real cualquiera. La dificultad de este detalle que presentamos en aquella oportunidad es notablemente superior a lo que ahora hemos presentado. Véase en la imagen siguiente lo que hace dos años planteamos.

Imagen N° 12
En complemento, el caso del año pasado, referida al 2023, tampoco fue elemental. Por otro lado, me parece que es el que reviste la peculiaridad más grande, como se incluye en la imagen siguiente. Resulta que la factorización en números primos de 2023 es así: 2023 = 7 x 17 x 17 = 10 x 71 x 172. Lo singular de la expresión es que los factores 7 y 17 vienen dados por: 7 = 2 + 0 + 2 + 3 y 17 = 22 + 02 + 22 + 32. Así, como se ve a continuación: 2023 = (20 + 00 + 20 + 30)0 x (21 + 01 + 21 + 31)1 x (22 + 02 + 22 + 32)2.

Imagen N° 13
Revisando el asunto, veremos que se trata, en definitiva, de una propiedad bastante extraña, sino es que única, en todo el conjunto ℕ de los números naturales. Es decir, es probable que no exista otro número natural que cumpla con una condición similar. Como apreciamos, el sentido matemático de las propiedades de un cierto número puede no coincidir con la visión popular del mismo.
En esta línea de ideas, en artículo previo mencionábamos la diferencia que se encuentra entre la escogencia de los babilonios por el número 12, para medir y contar, y la correspondiente de los mayas, que escogieron el 13. A primera vista, el 12, que se hizo popular en el Viejo Mundo, podría contener ventajas sobre el 13 maya. La visión matemática del punto es contraria a esta percepción.
Para ir cerrando, nótese que las factorizaciones en primos de los últimos ochos años son como sigue: 2017 = 2017 (es primo), 2018 = 2 x 1009, 2019 = 3 x 673, 2020 = 2 x 2 x 5 x 101, 2021 = 43 x 47, 2022 = 2 x 3 x 337, 2023 = 7 x 17 x 17, 2024 = 2 x 2 x 2 x 11 x 23. Aquí, varias conclusiones. No obstante, a vuelo de pájaro, notamos que este es el año que más factores primos contiene, pues se llega a cinco. Esto lo hemos descrito anotando: 2024 ∊ P5. De manera similar, apuntaríamos que: 2020 ∊ P4, 2023 ∊ P3, 2022 ∊ P3, 2021 ∊ P2, 2019 ∊ P2, 2018 ∊ P2, y, finalmente, 2017 ∊ P1, donde P1 viene a ser el conjunto de números primos.
Para finalizar, y para no quedarnos con la idea de que 2024 es un número soso, sin alguna propiedad un poco más interesante que esta de ser una diferencia de cuadrados (vimos que casi todos los naturales pueden ser colocado de esa forma), paso a colocarlo en una expresión un poco más particular, o especial, para hacerle un poco de honor al presente año. Resulta que la expresión factorizada puede ser manipulada para descubrir un secreto oculto en ella. Aquí la secuencia: 2024 = 23 x 11 x 23 = 2 x 2 x 11 x 2 x 23 = 2 x 2 x 11 x (12 / 6) x 23 = 4 x (1/6) x ( 11 x 12 x 23 ).
Resulta que una suma de números enteros consecutivos responde a la fórmula: 1/6 n (n+1) (2n + 1). Si se analiza, con n = 11, la prescrita fórmula asume, cabalmente, el valor: (1/6) x ( 11 x 12 x 23 ). Esto significa que la suma de los primeros 11 cuadrados dará por resultado (1/6) x ( 11 x 12 x 23 ) = 506. Es decir: 506 = (1/6) x ( 11 x 12 x 23 ) = 12 + 22 + 32 + 42 +… + 112. En otras palabras, dado que 2024 = 4 x 506, tendremos que: 2024 = 4 (12 + 22 + 32 + 42 +… + 112).
Un último arreglo nos lleva a la perseguida propiedad, a saber: 2024 = 22 + 42 + 62 + 82 + 102 +… + 192 + 202 + 222. Es decir, 2024 es la suma de los cuadrados de los primeros doce números pares, entiéndase: 2024 = 02 + 22 + 42 + 62 + 82 + 102 +… 202 + 222. Siendo 12 lo meses del año, márquese cada hoja del calendario con los números pares consecutivos, empezando por 0, que es par. Sustitúyase este número por su cuadrado. Así, obtenemos la siguiente secuencia: enero 0 = 02, febrero 4 = 22, marzo 16 = 42, abril 36 = 62, mayo 64 = 82, junio 100 = 102, julio 144 = 122, agosto 196 = 142, septiembre 256 =162, octubre 324 = 182, noviembre 400 = 202 y diciembre 484 = 222. Si se suman los 12 marcajes obtendremos 2024.








