Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
No hay enigmas. Si un problema puede plantearse, también puede resolverse.
Ludwig J. J. Wittgenstein
Es mucho sobre lo cual podríamos discurrir, aunque pretendemos un artículo breve y bastante conciso, que ojalá resulte transparente y clarificador. Se encuentra motivado por una nefasta confusión circulante, como muchas de las que suelen observarse hoy en las redes sociales. Como siempre, resulta sorprendente y admirable, no tanto la confusión, que puede ser explicada y entendida, con cierto grado de razonabilidad, sino más aún la extrema polarización y lo acalorado de las discusiones que se generan. Los bandos defienden, a capa y espada, lo que cada uno considera «la verdad», pero lo malo son las despectivas expresiones y la minusvalía que se dirige a la alteridad, la cual llega al insulto, directo o indirecto.
Se trata de una mediática confusión sobre una particular operación aritmética, bajo la temática de la jerarquía operacional. Se presenta una secuencia de operaciones aritméticas básicas, y se pregunta al interlocutor cuál es el resultado correcto de tal cuestión. El objetivo es crear polémica y discusión, pues, aparentemente, existen dos resultados posibles. Así, prontamente, los comentaristas se dividen en dos posiciones ante la supuesta ambigüedad. Además de este tema de la jerarquía de las operaciones aritméticas básicas, nuestro titular menciona la posverdad, que puede ser definida como una información, o afirmación, en la que el público tiende a priorizar las opiniones y emociones suscitadas por encima de cualquier posible objetividad en los contenidos involucrados. La RAE la define así:
Es un neologismo que implica la distorsión deliberada de una realidad, en la que priman las emociones y las creencias personales frente a los hechos objetivos, con el fin de crear y modelar la opinión pública e influir en las actitudes sociales.
A la posverdad también se le llama mentira emotiva. En el caso que trataremos, veremos que, en efecto, hay un acto de manipulación en el planteamiento, y a este respecto los medios de difusión tienen mucho que aportar, para bien y para mal. Desde que el interés primario no es la difusión de una narrativa que nos oriente a la construcción de verdad, sino que, al contrario, lo que se pretende es el incremento de seguidores, o likes, resulta razonable que las temáticas priorizadas sean aquellas que despierten la curiosidad, sin importar las ambigüedades, relativismos o confusiones, profundas a veces, que se puedan desarrollar a partir de la nota publicada. Léase «Infocracia: digitalización y crisis de la realidad».
Obsérvese que, en la anterior definición, se habla de una deliberación orientada a influir en las actitudes sociales. En el caso que estamos trayendo a colación, lo que se persigue es reforzar el nihilismo imperante, cimentado en el pleno auge del régimen de la información, en donde cualquier narrativa, o posible verdad, se vuelve relativa y dependiente de las circunstancias. Así, la Mfatemática, que se nos ha presentado como una ciencia exacta, será doblegada ante esta supernarrativa de la posverdad, en donde todo adquiere el tinte de los lentes con que se le vea. Unos plantearán una respuesta, mientras otros alguna diferente. Por ello, ya no existe más la supuesta y tácita «exactitud».
La operación aritmética planteada en el mediático post es 6÷2(1+2). Unos dicen que el resultado es 1, mientras otros opinan y apuestan porque es 9. Sorprende sobremanera que, en el intercambio en redes, se citó un artículo de BBC News Mundo, el cual describe la interrogante como esencialmente ambigua, esto es, que no existe un camino unívoco que arroje una respuesta única. Por ello el artículo «Por qué la solución a esta sencilla ecuación es tan problemática» me causó molestia, puesto que los errores en los que incurre se verán multiplicados por el gran número de lectores y lectoras. Para empezar, repárese que el título está errado, pues habla de una ecuación, que no existe en ningún lado.
Trataremos de explicar la naturaleza del supuesto problema, y la solución al equívoco. En el epígrafe hemos citado al austríaco Ludwig Wittgenstein, filósofo, matemático, lingüista y lógico austríaco, autor de la reconocida obra Tractatus logico-philosophicus, de gran influencia en la naciente Lógica contemporánea y en el Círculo de Viena. El asunto que nos ocupa refiere, de manera radical, al lenguaje, y en particular es temática lógica. Todo lenguaje se funda en convenios, pero es importante observar que una vez asumidos, estos deben mantenerse. Por ejemplo, las palabras «mesa» y «puerta» son arbitrarias (al margen de su etimología, evolución histórica y otros criterios de posible influencia), pero, una vez asumidos, nadie podría llamar «puerta» a una mesa o viceversa.
Igualmente sucede con los lenguajes formales, utilizados en Matemática, Lógica y Computación, las tres ciencias formales de la contemporaneidad. Estas ciencias, a diferencia de las ciencias factuales, no se refieren a hechos o realidades sensibles, del mundo empírico, como cuando hablamos del Sistema Solar, sino que tratan de asuntos abstractos, generalmente desarrollados deductivamente, a partir de convenios iniciales, de aceptación mundial. Por ello suele decirse que se trata de lenguajes universales, aunque algunos y algunas utilizan esta expresión para la música. Claro, en los lenguajes formales también hay convenios, pero, se asumen al inicio de la edificación, como cuando se escogen los axiomas, los objetos primitivos, la simbología y los convenios de escritura. La nueva Lógica ilustra perfectamente este proceder.
La actualidad de la posverdad, que hemos mencionado, opera de manera diferente. No se pretende o se persigue ningún tipo de universalidad, sino todo lo contrario. Se valida cada percepción y punto de vista como si todo, en cualquier momento, fuera convenible. Por ello es importante insistir en la contraposición. El nihilismo, en general, consiste en una corriente filosófica que sostiene la imposibilidad del conocimiento, negando la existencia y el valor de todas las cosas. En su versión contemporánea, se parte de la masiva disposición de datos para cerrar la puerta a la existencia de la verdad, como constructo epistemológico, generando un relativismo dependiente de cada interlocutor, sea por sus condiciones cognitivas particulares o de acuerdo a su perspectiva emocional.
Entremos en la concreción del asunto: procedamos a evaluar la expresión 6÷2(1+2). Quienes afirman que la respuesta es 1, argumentan que la expresión debe entenderse como: 6÷2(1+2) = 6 ÷ ( 2(1+2) ) = 6 ÷ ( 2 x 3 ) = 6 ÷ 6 = 1. En contraposición, los defensores de la alternativa del 9 lo explican así: 6÷2(1+2) = (6 ÷ 2) (1+2) = (6 ÷ 2) x 3 = 3 x 3 = 9. Primero, acotemos anotando que, en esta simbología, las separaciones no establecen jerarquía o prioridad alguna. Es decir, 6÷2(1+2), 6 ÷ 2(1+2) y 6÷2 (1+2) deben ser leídas, y entendidas, como expresiones equivalentes. Nótese que, en castellano, esto no es así, pues «máscara» no es lo mismo que «más cara». Los espacios sí importan acá.
El segundo punto es relativo a la expresión (1+2), la cual no forma parte del problema, pues equivale a 3, en cualquiera de todas las interpretaciones posibles. De esta guisa, el supuesto acertijo se reduce a: 6÷2(3). En este momento es importante reparar en un asunto medular, que termina siendo el meollo de la cuestión. Nótese que no se está pidiendo que el lector o lectora vaya a un computador, o calculadora, como es usual llamarle al asistente electrónico para cómputos numéricos, para averiguar que nos dice el aparato como respuesta a la interrogante. Y es que, una cosa es lo que una máquina pueda decirme, y otra la respuesta que desde el lenguaje aritmético estándar debe proporcionarse.
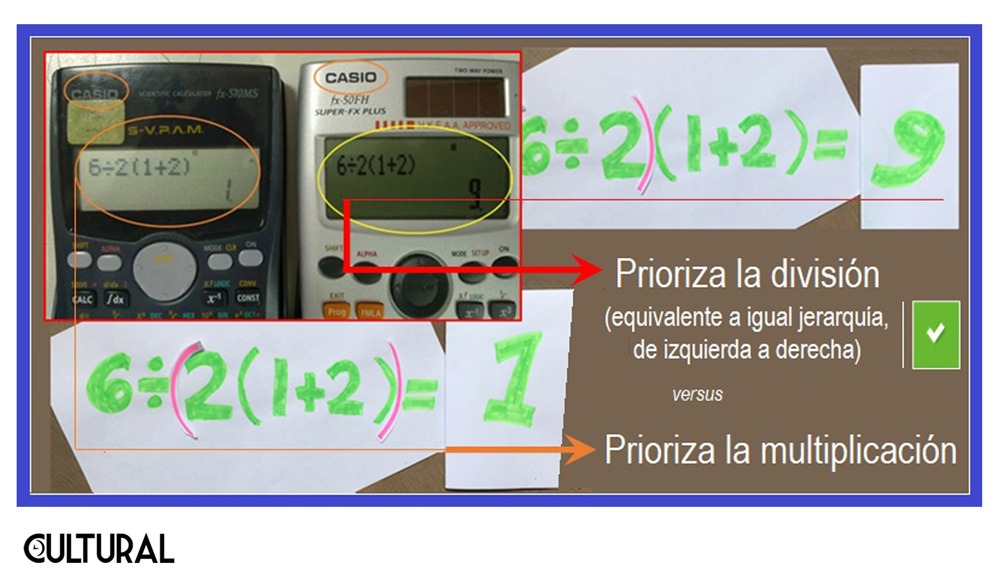
Resulta que, en efecto, algunos aparatos arrojan como resultado 1, mientras otros dicen que la respuesta es 9. Desde esta perspectiva, hemos de concluir que la pregunta es ambigua, o lo que es lo mismo, aceptar que la respuesta depende de cómo pueda entenderse, esto es, que se trata de un asunto relativo, dependiente de los contextos. Sin embargo, insisto, el enunciado de la pregunta está escrito en lenguaje aritmético estándar. En suma, es crucial separar lo matemático en la operación planteada de una posible asistencia de las calculadoras. El lenguaje matemático es, por lo general, universal y estandarizado, y en este nivel tan elemental no hay duda al respecto.
Por ello hablamos previamente de la forma en que se construye la Matemática, contraponiéndola a la manera en que la posverdad se desarrolla y opera en los distintos canales de compartición de opiniones. Si hemos de hacer un símil, deberíamos retrotraernos a Platón y su conocida distinción entre la episteme y la doxa. Nuestra contraposición inicial obedece a la que existe entre las convenciones aritméticas y el uso de las herramientas de cálculo, últimas en el contexto de la digitalización y la crisis de la verdad.
Que existan calculadoras con convenios de jerarquía distintos no establece que la comunidad matemática, muchísimo antes, haya resuelto la problemática de posibles ambivalencias o de polisémicas interpretaciones. Más que «exactitud», esto es lo que caracteriza a todas las ciencias formales: la eliminación de la ambigüedad que los lenguajes naturales poseen, mediante convenios de una casi universal aceptación. Siempre se permiten acepciones particulares, una vez sean establecidas y comunicadas, conveniente y pertinentemente, desde un inicio.
Pasemos a la explicación matemática. Las operaciones formales, no solo las numéricas sino otras en lógica y computación, suelen definirse de manera binaria, esto es, entre dos elementos, tomados en un cierto orden. Una operación binaria es una función que toma dos elementos del dominio, en un cierto orden, y les asigna, de manera unívoca y bien definida, un tercer elemento, llamado el resultado de la operación. Las operaciones usuales de adición, sustracción, multiplicación y división de números (se entiende que números reales) pueden ser definidas así.
La notación usual en la escuela y el álgebra básica (de expresiones con números reales) es infija. Esto significa que, por ejemplo, el resultado de la adición de 6 con 2, es decir, el número asignado a la pareja (6,2) bajo la adición se escribe así: +(6,2) = 6 + 2. El problema de la notación infija es que, si se desea realizar operaciones con más de dos elementos, se genera, de forma natural, una cierta ambigüedad, a menos que la operación sea asociativa, como es el caso de la adición. En general, una expresión como a □ b □ c no está bien definida, puesto que los procesos a □ (b □ c) y (a □ b) □ c no tendrían razón para coincidir.
De hecho, esto es lo importante de la propiedad de asociatividad. Se dice que la operación □ es asociativa si a □ (b □ c) y (a □ b) □ c coinciden, es decir, dan el mismo resultado, en cualquiera de todas las instancias para a, b y c. En Álgebra se estudia que los números reales constituyen, al igual que los números racionales (con los que operan las calculadoras), una estructura algebraica de campo, o cuerpo. En esta estructura se parte de dos operaciones binarias, únicamente de dos, llamada adición y multiplicación. Ambas son asociativas, por lo que es posible construir cadenas operacionales de longitud arbitraria, tanto para sumas como para productos. Expresiones como 6 + 2 +3 o 6 x 2 x 3 tienen total sentido, pues son unívocas. Los resultados son 11 y 36, respectivamente, y acá nadie discute nada.
Con la notación infija, para indicar el orden que se desea seguir, las operaciones no asociativas (que es lo usual) necesitarán recurrir al uso de los paréntesis. Es un tema de lógica, más que de matemática. También aparece en el condicional, o implicación, utilizado en computación. La estructura sintáctica if … then requiere de convenios específicos en cada lenguaje de programación, porque la expresión a □ b □ c resulta ambigua para el caso en que □ simbolice la implicación. Una sobresaliente forma de evitar este problema, es recurriendo a la denominada notación polaca. Para no extendernos en esto, y para fortalecer la exposición, cito un extracto del enlace anterior, a la Wikipedia:
El lógico polaco Jan Łukasiewicz inventó esta notación, alrededor de 1920, para simplificar la lógica proposicional. Una cita de Axiom and Generalizing Deduction de Jean Nicod, expone: «Vine sobre la idea de una notación libre de paréntesis en 1924. Utilicé esa notación por primera vez en mi artículo Łukasiewicz». […] Alonzo Church menciona esta notación en su libro clásico sobre lógica matemática, como digna de observación en los sistemas notacionales, incluso contrastados con los incluidos en los trabajos Exposición lógica notacional y Principia Mathematica, de Alfred Whitehead y Bertrand Russell.
Aunque no es lo frecuente, las notaciones polacas, sean prefijas o postfijas, se implementaron en algunas calculadoras, como las antiguas de Hewlett-Packard Company. La expresión a □ (b □ c) se escribiría, en notación prefija, como □ a □ b c, mientras que (a □ b) □ c se escribiría así: □ □ a b c. Nótese que no se utilizan paréntesis y, aun así, no hay ambigüedad. Sin importar si □ es asociativa, es posible escribir cadenas sin recurrir al uso de los paréntesis. Empero, por lo complicado de la traducción de la notación infija a la prefija, usada en la escritura algebraica estándar, la usada en la secundaria, los calculadores abandonaron el uso de la pre o post operación.
Regresando a la axiomática matemática, nótese que no se habla ni de sustracción ni de división. Esto porque no se requiere de las mismas y porque no poseen propiedades que faciliten el manejo de las expresiones. Lo que la axiomática contempla es la existencia de inversos, tanto aditivos como multiplicativos (con la excepción de 0, que no posee recíproco). Una expresión como 6 – 2 se interpreta como una adición, justamente como la suma de 6 con –2: 6 – 2 = 6 + ( –2 ) = 4. Por ello la adición y la sustracción serán, en esencia, la misma operación. Una expresión ternaria como 6 – 2 +3 no es ambigua, puesto que se lee como la suma de 6, –2 y 3: 6 – 2 + 3 = suma (6, –2, 3) = Σ (6, –2, 3) = 7.
Por ello, para los matemáticos (i.e. en el interno de la Matemática, como ciencia formal), la expresión 6÷2(3), en la que nos quedamos, no representa ni conlleva tampoco ninguna ambigüedad. Acordado que la yuxtaposición de dos símbolos semánticamente autónomos, o separados mediante paréntesis, implican una multiplicación, no habría confusión posible. Es decir, asumiendo que ab = a(b) = (a)b = a x b, denota el resultado de la multiplicación de a por b, se tiene que 6÷2(3) equivale a escribir 6÷2×3. Al igual que 6 – 2 + 3, 6÷2×3 = 6 ÷ 2 x 3 no presentará ninguna múltiple interpretación.
La división se realiza mediante una multiplicación, y la operación se define así: a÷b = a/b = ab– 1 = a x b– 1. En algunos países se usa a:b para a÷b. En el álgebra básica se prefiere el uso de la raya, que, además de ser clara, por sí misma, funciona como agrupador. En cualquiera de los casos, 6 ÷ 2 significa la multiplicación de 6 por el inverso multiplicativo de 2, que es ½ (2–1 = ½), puesto que 2 x ½ = 1. Por ello: 6 ÷ 2 = 6 x 2– 1 = 6 x ½ = 3. De similar forma, no hay problema con una expresión ternaria como 6 ÷ 2 x 3, puesto que se lee como el producto de 6, 2–1 y 3. Así, tenemos que: 6 ÷ 2 x 3 = producto (6, 2–1, 3) = Π (6, 2–1, 3) = 9.
Si alguien quisiera insistir en la ambigüedad de la expresión 6 ÷ 2 x 3, o que esta podría tener como resultado 1, debería entonces aceptar, en perfecta analogía, que 6 – 2 + 3 también lo es. Para que 6 ÷ 2 x 3 tenga por resultado 1, la expresión debe ser leída como 6 ÷ ( 2 x 3 ), que equivaldría a interpretar 6 – 2 + 3 como 6 – ( 2 + 3 ), también daría 1. No obstante, hemos aprendido que – 2 es un único elemento, que simboliza el inverso aditivo, o negativo, de 2. Estos operadores unitarios tienen jerarquía, o precedencia, sobre las operaciones binarias.
De manera en lo absoluto igual a como sucede con – 2, acontece con el símbolo ÷, pues ÷ 2 debe ser entendido como el operador unitario ÷ aplicado a 2, esto es, como el inverso multiplicativo, o recíproco, de 2, que es ½. Esto es así en función de la axiomática estándar del campo de los números racionales (o, si se quiere, del campo de los números reales o de los números complejos). De esta forma, cualquier instancia del signo ÷ se lee, e interpreta, como una multiplicación con el inverso multiplicativo, o recíproco, del elemento que le sigue. Los axiomas exigen el cumplimiento de que 2 + ( – 2 ) = 0, por un lado, y que 2 x 2–1 = 2 x ½ = 1.
En suma, al cuestionarnos por el valor de la expresión 6÷2(1+2), lo que leemos es un producto de tres factores, a saber, el producto de 6, 2–1 y 3. Entiéndase entonces que, así como 6 – 2 + 3 = Σ (6, –2, 3) = 7, en perfecta analogía tenemos que 6 ÷ 2 x 3 = Π (6, 2–1, 3) = 9. Empero, conviene anotar un detalle más, relacionado con el creciente y preocupante distanciamiento entre el quehacer matemático formal y la enseñanza escolar de la matemática básica, o, si se prefiere, entre la Matemática como ciencia, robusta y caracterizada por su rigor lógico, y el uso que en lo cotidiano se hace de aplicaciones elementales. Se recomienda al inquieto lector, lectora, una detallada revisión del tema, pinchando aquí, pero preferiblemente en la versión en idioma inglés. Allí, citando precisamente este caso, se lee:
Un ejemplo cobró reciente popularización viral en relación con una operación de la que surgían dos resultados diferentes, según la calculadora empleada: la ambigüedad de su notación, sin embargo, se suple apelando a las indiscutibles propiedades de las operaciones.
La jerarquía aritmética operacional refiere a ciertos convenios sobre facilidad de escritura. Básicamente la multiplicación precede a la adición. Así, la expresión a + b x c se entiende como a + ( b x c) y no como ( a + b) x c. Esto se debe, fundamentalmente, a la propiedad de distributividad del producto respecto a la suma, en vista que la suma no es distributiva respecto al producto, con lo cual la simetría sería completa, como en el caso de las álgebras booleanas, otra estructura algebraica diferente a la de un campo.
La distinción entre multiplicación y adición aparece en la estructura algebraica de anillo, en donde la «división» tiene sentido únicamente cuando existen los inversos multiplicativos, como es el caso en la estructura del campo de los números reales. Seguro regresaremos a todo esto en una próxima oportunidad, en vista que se nos ha agotado el espacio, pues varios puntos importantes pueden ser abordados a partir de lo ahora compartido.
Subrayamos que la confusión básica, explotada en los memes en internet, se debe a que en distintos países se implementan reglas o convenciones que, apelando a una posible simplificación, dejan la puerta abierta para algunas erróneas interpretaciones. Es el caso del acrónimo, en idioma inglés, pemdas (equivalente al papomudas en español), que se acuña como mnemotecnia para el orden a seguir en la evaluación de expresiones aritméticas mixtas, léase: paréntesis, exponentes (o potencias), multiplicación, división, adición, sustracción. El problema es que la correcta interpretación es: paréntesis, exponentes/potencias, multiplicación/división, adición/sustracción. O sea, lo que hemos dicho acá, que la multiplicación y la división tienen jerarquía equivalente, al igual que la adición y la sustracción.
Si en la expresión 6÷2(1+2) priorizas la multiplicación por encima de la división, el resultado dará 1. Si priorizas la división, el resultado será 9. Lo que sucede es que, por la arquitectura de los calculadores, resulta conveniente establecer una prioridad explícita para cada operación, es decir, para cada tecla. Las confusiones se agravaron cuando los calculadores incluyeron los símbolos de paréntesis, tanto para agrupación como para denotar el producto. Enfatizamos que la dificultad, o más bien, los equívocos y ambigüedades, aparecen cuando el usuario traduce una cierta expresión a una secuencia de teclas. No obstante, insistimos, desde la simbología aritmética aceptada universalmente, la expresión 6÷2(1+2) contiene tres factores, que dan como producto 9.

Sobre la posverdad, el filósofo, humanista y pensador británico, Anthony C. Grayling, asegura que la posverdad tuvo su origen en la crisis económica norteamericana del 2008, debido a los resentimientos que despertó, facilitando la exaltación de las emociones sobre temas como la inmigración, sembrando a su vez dudas sobre el actuar de los políticos. Grayling también asegura que otro ingrediente clave en la cultura de la posverdad son las redes sociales, como lo estamos señalando acá. Curioso es que, hace seis años, la BBC News Mundo publica un artículo en el cual, citando a Grayling, advierte sobre los peligros de la posverdad. Que años después se oriente en la dirección contraria me parece, no solo peligroso, sino contraproducente.
Para cerrar, pienso que lo importante en todo esto es el reconocimiento de que no hay paradoja posible, de la que podríamos extraer nuevos conocimientos, como ha sucedido en otros tiempos, que la notación y el lenguaje matemático, o científico, no se encontraban a la altura del rigor requerido, exigiendo nuevos desarrollos. Más bien, es como apunta Wittgenstein en la cita inicial: no hay enigmas.
Fuente de imágenes ::
[ 1 + 2 + 3 ] Imágenes editadas por Vinicio Barrientos Carles :: https://www.bbc.com/mundo/noticias-49168226 + https://plus.maths.org/content/pemdas-paradox + https://www.mathnasium.com/eagan/news/what-pemdas-e + https://abbreviations.yourdictionary.com/what-is-pemdas-order-operations-rules-simple-terms + https://sebbm.es/rincon-del-aula/contra-la-posverdad/








