Vinicio Barrientos Carles
Guatemalteco de corazón, científico de profesión, humanista de vocación, navegante multirrumbos… viajero del espacio interior. Apasionado por los problemas de la educación y los retos que la juventud del siglo XXI deberá confrontar. Defensor inalienable de la paz y del desarrollo de los Pueblos. Amante de la Matemática.
La memoria más fuerte será aquella basada en imágenes.
Ramón Campayo
Contrario a la voz popular, la importancia de la Matemática no radica en la realización de cálculos, sobre cómo hacerlos y la exactitud de los mismos. Esta concepción que usualmente se tiene de la Matemática ha derivado, en múltiples y muy diversas malas consecuencias. La principal es la mala orientación de todas las prácticas educativas, que tiene como principal corolario el rechazo de la mayoría de la gente, no encontrándole la belleza que corresponde a tal disciplina, tirando por la basura los grandes beneficios, intelectuales, cognitivos y emocionales que posee, de forma inherente, el quehacer matemático.
Dicho con otras palabras, cualquiera imagina que el quehacer matemático es realizar cálculos. En varios artículos, y en especial los de nuestra columna Quadrivium, hemos insistido que el sentido de su comprensión, y los objetivos educacionales, no deben estar orientados al aprendizaje y aplicación de algoritmos. Un problema matemático se concibe, erróneamente, como un planteamiento de una situación en donde se te dan unos datos, de tipo numérico, y se te pide que los combines, y mediante la aplicación de un algoritmo, realices cálculos y des, al final de los procesos, un resultado, también de tipo numérico.
Esto se encuentra alejado de la realidad del genuino quehacer matemático. Primero, de una manera más general, no se trata de un asunto exclusivamente de números, sino de verdades lógicas, esto es, de fuerza, que necesariamente se tienen que dar, dadas unas condiciones y un contexto determinado. Claro, algunas de estas verdades se encuentran en la temática de los números, pero esto no es únicamente así. Las premisas que en un determinado sistema matemático se asumen como punto de partida se llaman axiomas, y el objetivo de la actividad es descubrir teoremas, que son las verdades que forzosamente se tendrán que dar, dado que se han aceptado los axiomas.
Este trabajo deductivo, de conjetura y de argumentación, es como en los juegos de salón u otros, en los que se ponen ciertas reglas, y al cumplirlas, se van descubriendo situaciones, que no son fortuitas o contingentes, sino que lógicamente tendrán que darse. En esta dinámica surge y puede apreciarse la naturaleza lúdica de «lo matemático». Esto suena a locura, porque el lector, lectora, que nos lee, con seguridad, al evocar lo matemático tendrá un cúmulo de sensaciones tortuosas y de gran complicación emocional. Pero estamos esperanzados en que esto, y más temprano que tarde, cambiará. Ahora estamos acercándonos al meollo de lo matemático: la demostración.
La razón para que estas realidades mecanicistas se vean modificadas drásticamente, en el mediano plazo, radica en algo sobre lo que hemos estado conversando, y bastante, últimamente: el advenimiento de la inteligencia artificial. En efecto, la IA ha venido a ampliar los horizontes de ejecución, mecánica, que iniciaron décadas atrás, cuando apareció la calculadora. Pronto los ordenadores, disponibles para todo el mundo, podrán realizar la resolución de cualquier problema algorítmico. Esto muchos lo ven como una amenaza, pero en mi particular percepción, lo veo como una situación esperanzadora, porque los seres humanos nos veremos empujados a realizar actividades inteligentes y creativas, dejando de lado todo ese bagaje de aplicaciones mecanicistas (y alienantes) que arriba estoy criticando.
En otras palabras, dejaremos de dedicarnos a la ejecución de tareas automatizables, abandonando los comportamientos tipo autómata, y permitiendo que las máquinas hagan ese tipo de trabajo. Lo mejor para comprender todo esto que estoy intentando trasladar será colocar un ejemplo. En la escuela elemental aprendimos que los tres ángulos internos de un triángulo suman dos rectos, esto es, 180°. Los esfuerzos educacionales se concentran, primero. en la memorización del teorema: «dados α, β y γ las medidas de los tres ángulos de un triángulo plano cualquiera, se tiene que α + β + γ = 180°»
Paso seguido, los ejercicios y «problemas», consisten en aplicar tal verdad matemática, como es el caso de entregar los valores de un par de ángulos, y solicitar el tercero. ¿Qué se debería hacer? Pues realizar juegos exploratorios y llevar al estudiante al descubrimiento de tal teorema, pero, más aún, hacia la comprensión de por qué esto debe ser así, por qué es necesario que se de esta situación. Dicho en otras palabras, al descubrimiento de una demostración de tal teorema. Esto no es complicado, por extraño que parezca. Casi nadie, creo yo, puede demostrar tal hecho, aunque muchos y muchas sí lo conocen.
El lector y lectora se sorprenderá al respecto de lo fácil, e interesante, que podría resultar una demostración, y una de tipo visual, como las que hoy deseamos abordar. Bastaría trazar una paralela a alguno de los lados para caer en la cuenta de que el teorema debe cumplirse. Literalmente, se «puede observar» por qué es así. Sin embargo, aunque las demostraciones develan mucho de lo importante en tal o cual teorema, el proceso de elaboración de conjeturas es también muy importante. Reflexionar sobre las condiciones que deben darse, también aporta.
¿Qué es un triángulo? Si tomamos tres puntos cualesquiera (del espacio), y los conectamos, unimos, mediante segmentos de recta, si estos no quedan sobre la misma recta, formarán un triángulo. Pareciera que no hay mucho que decir al respecto. Sin embargo, la historia de la ciencia y del pensamiento nos han evidenciado lo contrario. Desde el punto de vista matemático, eso de «no quedar en la misma recta» generó una idea muy interesante: la linealidad.
Por otro lado, acá estamos asumiendo que la noción de recta, o segmento de recta, está perfectamente definida y no queda lugar para ninguna ambigüedad. Aún si se relacionara la rectitud del segmento con la distancia mínima que puede trazarse, pareciera quedar unívocamente definido el asunto. La Matemática trata sobre conceptos, sobre sistemas deductivos de conceptos. Si se toman tres puntos sobre la superficie terrestre, veremos que, a veces, solo a veces, se cumple el teorema anterior, como en tres puntos de un determinado parque, pero no siempre es así. Para lo segundo, tómense tres puntos lo suficientemente separados, y nos sorprenderemos sobre lo que pasa.
Toma una pelota, o mejor si te consigues un globo terráqueo. Escoge, a continuación, dos puntos distintos sobre la línea del ecuador, y toma el tercero justamente en el polo norte. Únelos, caminando en línea recta, sobre la superficie de la maqueta del planeta Tierra, como lo harías si recorrieras en automóvil, o en avión, a 10 km de altura, y verás que cada uno de los ángulos formados son rectos, es decir, de 90°, por lo que los tres ángulos interiores del triángulo formado suman 270°… no 180° como te enseñaron en la escuela. Lo que ha sucedido es que se trata de un triángulo curvilíneo, esférico específicamente.
En la situación planteada, las rectas, las distancias más cortas, son las geodésicas, pero estas geodésicas no son planas (¿has escuchado acaso que nuestro universo es curvo?). No estamos hablando cuestiones fuera del mundo, estamos hablando de las cosas más naturales de nuestro entorno, sea inmediato o sea más allá de los confines de nuestro sistema solar. De donde sí nos estamos saliendo, es el reducido mundo de la escuela, el que hoy por hoy deberíamos cuestionar profundamente. Seguro podremos extendernos más sobre lo que hemos colocado como un ejemplo. Lo importante hasta aquí, los procesos de prueba, como parte del desarrollo crucial de los conceptos. Las máquinas pueden calcular, procesar algorítmicamente, pero no desarrollan intuición ni conceptos. Aquí lo fundamental.
El largo preámbulo, no solo es necesario, sino muy valioso para quienes nos siguen. Más de alguien me ha escrito diciendo, «todo muy bonito, pero cuando empiezas con “lo matemático”, me bloqueo… yo nunca serví para esas cosas». Por ello hacemos estas extensas aperturas, para ir ensanchando el camino y ampliando la aceptación de nuevas formas de entender la ciencia, las disciplinas formales, y de manera especial, la Matemática. Y sin más pasamos al tema de esta ocasión: las demostraciones visuales. También se les llama demostraciones gráficas, y otros hablan de geométricas, y se refieren a una modalidad de prueba de un hecho matemático que resulta evidente cuando se reflexiona detenidamente en un diagrama o esquema.
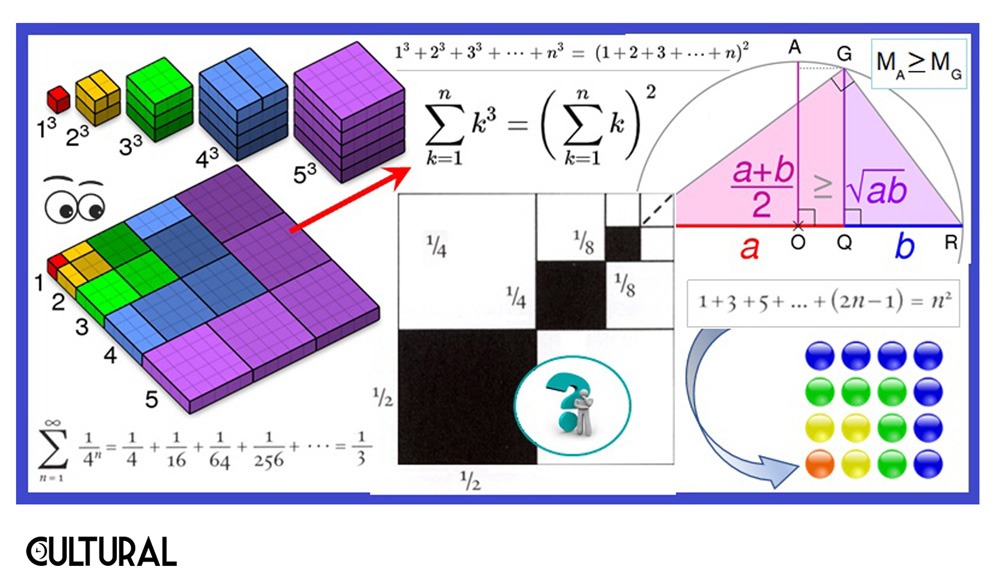
Empecemos con un par de casos sencillos. El primero, muy apreciado por los pitagóricos, refiere a los números impares. Lo hemos mencionado en el artículo «El teorema de los números poligonales», un caso particular de los números figurados. Véase la imagen que sigue, en la derecha, arriba. Se tiene un cuadrado de puntos, o circulitos. En el dibujo, se trata de un cuadrado de lado 6, que esta descompuesto en 6 hileras angulares. Si se repara, cada hilera de estas tiene un número impar de puntos. Se trata de los 6 primeros números impares, del 1 al 11. Esto es un hecho general, los primeros n números impares sumaran un cuadrado perfecto, cabalmente n2.
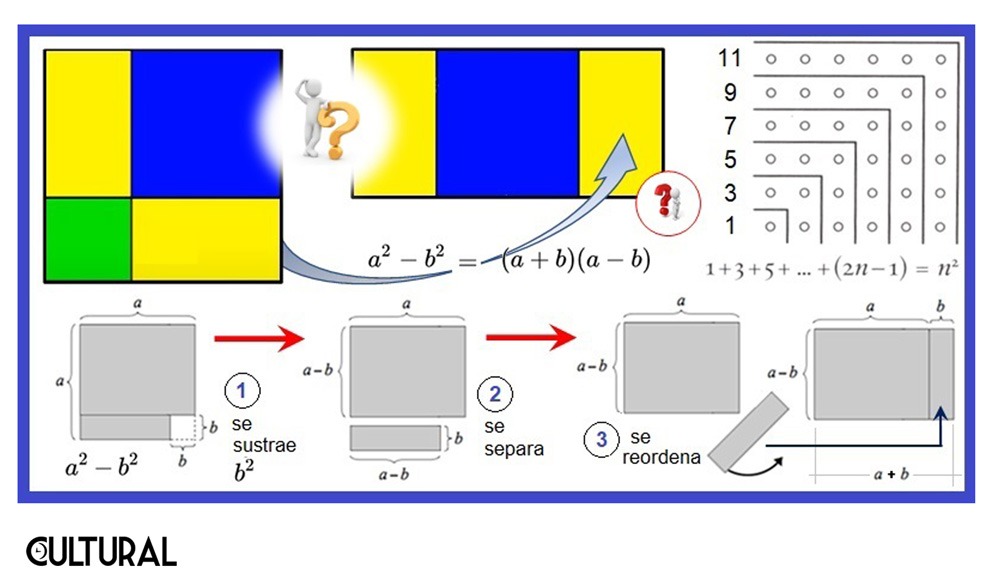
El resto de la imagen precedente contiene una prueba visual de una identidad estudiada en la secundaria: a2 – b2 = (a – b) (a + b). Nuevamente, quizá no resulte extraña, pero nunca nos pidieron o presentaron una demostración. La imagen proporciona una, y la secuencia de abajo pretende guiarnos sobre la equivalencia. En la parte coloreada se puede ver que si al cuadrado grande (en tres colores), que representa a2, le quitamos el cuadradito verde, que representa b2, nos quedarán las tres regiones, que acondicionadas forman un rectángulo de lados (a – b) y (a + b) respectivamente. El área amarillo-azul de la izquierda vale a2 – b2, mientras la de la derecha es (a – b) (a + b).
Recapitulando, en lo previo nos hemos tomado un buen espacio para orientar las motivaciones. Por un lado, que nuestras formaciones escolares no nos han orientado hacia la demostración matemática, dirigiéndonos a una mecanicista práctica de aplicaciones de algoritmos, que tampoco tenemos idea de dónde es que salen. Así, se ha tratado de una educación acrítica y para nada conceptual. De ahí que no sea extraño que nuestras concepciones de la Matemática, o de la ciencia en general, estén fuertemente sesgadas. El objetivo ahora es presentar unas demostraciones visuales, en rescate de la comprensión de los teoremas, de cómo podemos estar claros que las situaciones deben ser como se afirma.
En el caso de la imagen anterior, se muestra una prueba de una famosa identidad, que usualmente se aprende cuando estamos en el ámbito de la factorización en el álgebra de números reales. Una demostración simbólica iría, usando la propiedad distributiva de la multiplicación respecto a la adición, así: (a – b) (a + b) = a2 – ba + ab – b2 = a2 – b2. Se observa que esta igualdad se da porque: – ba + ab = ab – ba = 0, o lo que es equivalente, porque ab = ba. Empero, esta igualdad dependerá de qué objetos se simbolice con a y b, y de qué operación de multiplicación se esté hablando.
De hecho, para que la identidad sea verdadera, es condición necesaria y suficiente que la multiplicación sea conmutativa. Si a y b son números (reales o complejos), la multiplicación es conmutativa, pero si se tratara de otros objetos, como matrices, por ejemplo, la identidad de la diferencia de cuadrados no será cierta. Esto, en álgebra abstracta, se dice afirmando que una condición necesaria y suficiente, esto es, lógicamente equivalente, para que una estructura algebraica de anillo sea conmutativa, es que la identidad de la diferencia de cuadrados se cumpla en todos los casos. Como estamos señalando arriba, las matrices no forman un anillo conmutativo, puesto que, en general, la identidad AB = BA no se cumple, dadas A y B matrices.
Hay muchos casos de demostraciones visuales, y debe comprenderse que los esquemas o dibujos no deben ser tomados de manera específica o particular, sino generalizables a cualquier situación a la que refiera el teorema que se está demostrando. Es el caso del dibujo previo que mostraba los 6 primeros números impares, colocados de tal forma que conforman un cuadrado, precisamente de lado 6, demostrando que: 1 + 3 + 5 + 7 + 9 + 11 = 36 = 62. No obstante, la demostración visual se puede, fácilmente, repetir o imaginar para los casos n = 5, n = 13 o en cualquiera otro. Es decir, el proceso es generalizable a cualquier número natural n, de manera que se constituye en una prueba abstracta, afirmando que: 1 + 3 + 5 + … (2n – 1) = n2. Nótese que el n-ésimo número impar es 2n – 1.
Veamos otro ejemplo de demostración visual, uno diseñado para probar una serie geométrica convergente, esto es, la suma de un número infinito de términos decrecientes en una razón fija, es decir, en secuencia exponencial decreciente. Aunque se puede diseñar una demostración para el caso general de una secuencia decreciente en razón 1/n, la imagen que sigue muestra el caso la razón ¼. Esto es, que cada término en la sucesión será ¼ del anterior, de manera que los términos se van haciendo más chicos, hasta que, «en el infinito» se vuelvan 0, o virtualmente 0, porque la sucesión nunca termina y, en rigor, no se tiene un último término. ¿Cómo vamos a visualizar algo así?
Bueno, empiécese reparando en lo que se busca, que es la suma de esta sucesión infinita de términos. Parece de locos, nuevamente. ¿Cómo voy a sumar una sucesión de números que nunca termina? A ver, concreticemos lo que se me está pidiendo. Empiezo con un número, que por conveniencia tomaremos por ¼, e iremos generando el siguiente sacando la cuarta parte del precedente. Tendremos el siguiente conjunto sucesión: { 1/4, 1/16, 1/64, 1/256 … }. Aunque los términos se van haciendo más chiquitos, esto no nos garantiza que la suma de ellos convergerá a algún valor (esto es un problema matemático notable, véase «Las paradojas del movimiento de Zenón»).
Resumiendo, se pide que encontremos, y demostremos, el resultado de una posible suma, que sería: 1/4 + 1/16 + 1/64 + 1/256 + … Pásese a ver, entonces, la esquina superior derecha de la imagen que sigue. Se tiene un cuadrado y se construye, como se ilustra, una secuencia de particiones en forma de escuadra, a manera de un fractal, puesto que, si se analiza, se trata de una estructura que se repite infinitamente. Se parte el cuadrado inicial en cuatro cuadrantes, formando la primera escuadra con tres de los subcuadrados, dejando en pendiente el cuarto. Con este cuarto cuadrado, se vuelve a proceder igual, se subdivide en otros cuatro cuadrantes, tomando tres y apartando el último. Por ello en la esquina superior derecha se observa una secuencia de cuadraditos cada vez más pequeños.
Lo interesantísimo del esquema, ad infinitum, es que, al sombrear en obscuro el cuadrado central de cada una de las escuadras que se van formando, obtendremos la identidad que estamos buscando, porque vemos que, por cada cuadro negro, hay dos blancos; por cada uno sombreado, tenemos dos que no lo están. Entonces queda claro que el área sombreada será 1/3 del total, porque es una negra cada tres, al ser dos blancas. Así, en la imagen, se aprecia que el área negra es 1/3 del área total del cuadrado inicial.

Ahora bien, como se mira, cada cuadrado negro tiene por lados ½ del lado anterior. Así, el primero es ½ x ½ = ¼. De similar forma, el segundo ¼ x ¼ = 1/16; 1/8 x 1/8 = 1/64, etcétera. El área negra, que es la suma de los infinitos cuadraditos negros obtenidos, podrá ser escrita como una suma, infinita, de las áreas de cada uno de esos cuadraditos. Por ello, es posible concluir que: área negra = 1/4 + 1/16 + 1/64 + 1/256 + … Pero hemos observado antes que esta área negra es exactamente 1/3, de donde se ha demostrado, visualmente, que: 1/4 + 1/16 + 1/64 + 1/256 + … = 1/3, como se indica en la imagen.
También hemos colocado en la imagen la demostración visual de una desigualdad muy importante, la denominada desigualdad aritmético-geométrica, que afirma que el promedio geométrico de una cierta cantidad de números reales positivos no puede ser mayor que el promedio aritmético de esos mismos números. Dicho de otra manera, si MA es la media aritmética de una colección de números, y MG es la media geométrica, entonces el teorema afirma que MA > MG, o, en sumo caso MA = MG. De hecho, la igualdad se da cuando, y solo cuando, todos los números son iguales.
Recuérdese que la media aritmética, el promedio usual, se obtiene al sumar los números y dividirlos en el total, mientras que la media geométrica, o promedio geométrico, se calcula multiplicando los números y sacando la raíz correspondiente a la cantidad de números en el proceso. Un ejemplo ayudará. Dados 1, 2 y 4, la suma es 7 y el producto es 8. Así, MA = 7/3 = 2.33… mientras que MG deberá ser la raíz 3, raíz cúbica, de 8, lo que da MG = 2. Lo que dice el teorema es que ya sabíamos que MG tendría un valor menor que MA. Sobre la interpretación y lo que dice el diagrama previo, convendrá regresar posteriormente, para no congestionar demasiado el artículo.
Para ir cerrando, pero no dejar en la inquietud al más ávido lector o lectora, únicamente queremos indicar que la imagen inicial muestra un caso singularmente hermoso, referido al teorema de Nicómaco, tratado en el artículo «El triángulo aritmético de Fibonacci», invitándote a que leas las dos partes, en las que también hablamos de los números figurados. Aunque quedamos con varios pendientes, estamos en la expectativa de despertar la curiosidad para un ocio bien orientado. Después de todo, cuando preguntábamos si la IA desplazará al ser humano, insistíamos en un cambio hacia nuestra visión de quiénes somos, revalorizando nuestras competencias no automatizables, en rescate de la creatividad y las relaciones más profundas en las ideas.
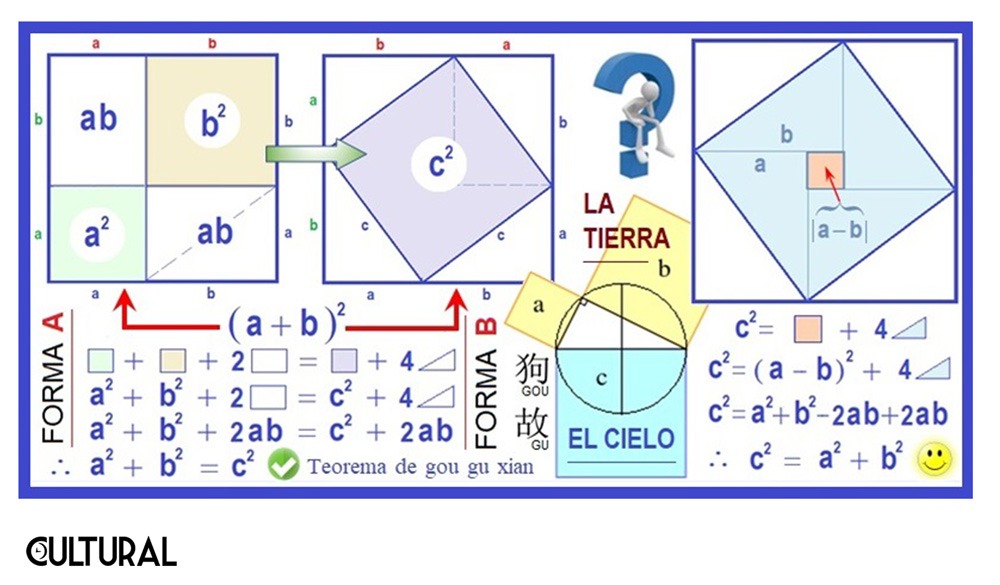
En otro artículo similar, «Calculando la hipotenusa: el teorema de gou gu xian», trajimos a colación que, para ejemplificar este nocivo y nefasto distanciamiento de las demostraciones matemáticas, visuales o no, casi todos y todas sabemos el enunciado del que identificamos como teorema de Pitágoras. No obstante, aunque hay varias demostraciones visuales del mismo, no las conocemos, por lo que el tal teorema viene a ser como un dogma, una verdad que tenemos que aceptar, porque sí. Arriba, y en el artículo mencionado, se puede ver un par de maneras visuales que hacen evidente lo que el teorema afirma, sea cualquiera que sea el triángulo rectángulo (plano) del que se trate.
Fuente de imágenes ::
[ 1 ] Imagen editada por Vinicio Barrientos Carles :: https://es.wikipedia.org/wiki/N%C3%BAmero_figurado + http://micaelgallego.blogspot.com/2006/11/pruebas-visuales-de-teoremas-matemticos.html + https://fr.wikipedia.org/wiki/Fichier:Nicomachus_theorem_3D.svg
[ 2 ] Imagen editada por Vinicio Barrientos Carles :: https://www.youtube.com/watch?v=tRJEMFkyF0Y + https://es.wikipedia.org/wiki/Diferencia_de_dos_cuadrados#Demostraciones_geom%C3%A9tricas + http://micaelgallego.blogspot.com/2006/11/pruebas-visuales-de-teoremas-matemticos.html
[ 3 ] Editado :: http://micaelgallego.blogspot.com/2006/11/pruebas-visuales-de-teoremas-matemticos.html + https://es.wikipedia.org/wiki/Desigualdad_de_las_medias_aritm%C3%A9tica_y_geom%C3%A9trica
[ 4 ] Imagen tomada de gAZeta, elaborada por vbc :: https://www.gazeta.gt/calculando-la-hipotenusa-el-teorema-de-gou-gu-xian-ii/







